数学模块综合测试

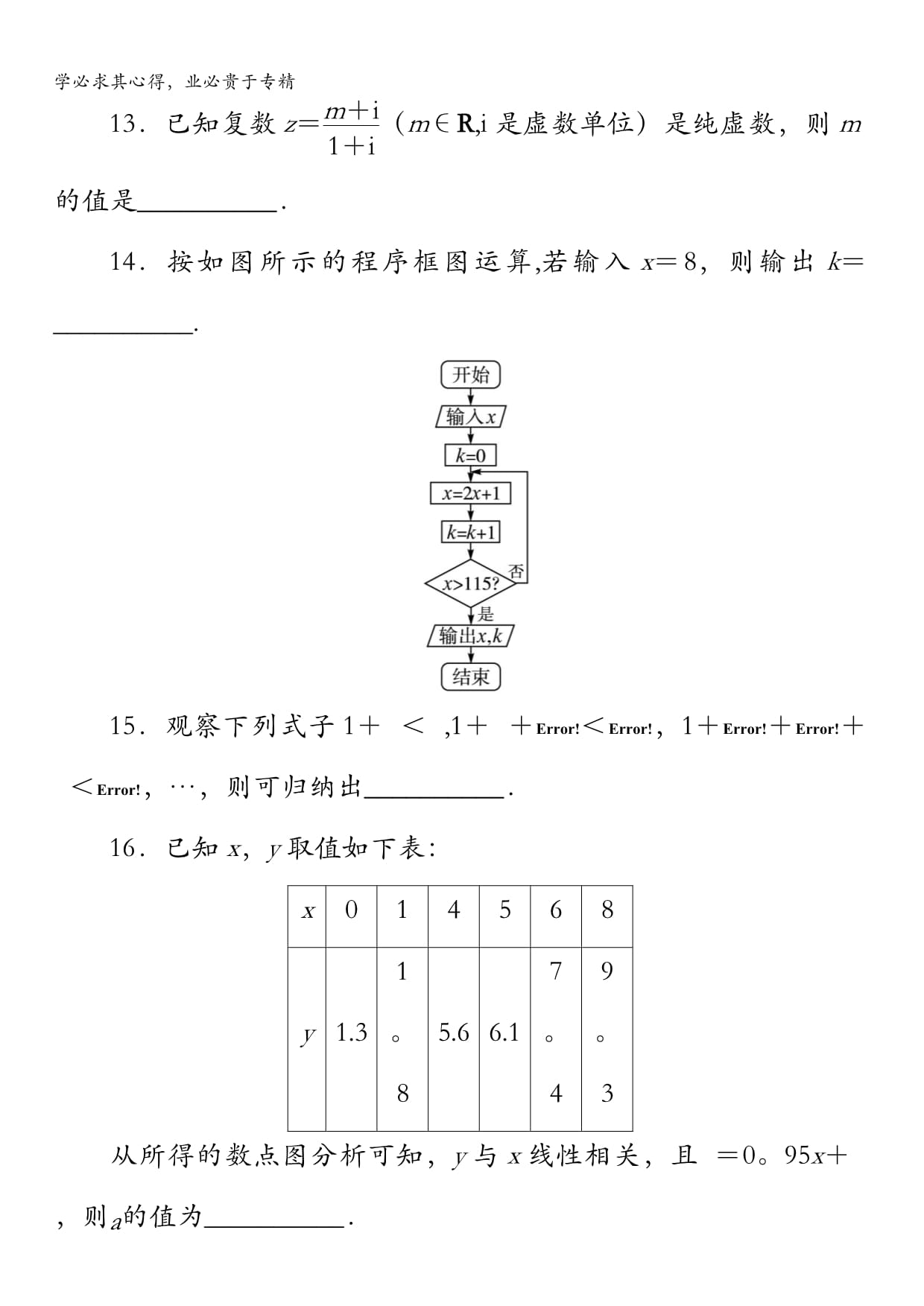
学必求其心得，业必贵于专精学必求其心得，业必贵于专精学必求其心得，业必贵于专精模块综合测评（一)（时间：120分钟满分:150分)一、选择题（本大题共12小题，每小题5分，共60分)1．已知复数z1＝2＋i,z2＝1＋3i，则复数z＝eq\f(z1，z2）在复平面内所对应的点位于(）A．第一象限B．第二象限C．第三象限D．第四象限2．eq\b\lc\｜\rc\|(\a\vs4\al\co1(\f(1，2－i）））等于(）A．eq\r（5)B．eq\f（\r（5），5)C．eq\f(1,5）D．13．下列说法错误的是()A．球的体积与它的半径具有相关关系B．计算误差、测量误差都将影响到残差的大小C．在回归分析中R2的值越接近于1，说明拟合效果越好D．在独立性检验中，K2的观测值k越大,说明确定两个分类变量有关系的把握越大4．在△ABC中，eq\o(AB，\s\up6（→）)＝a，eq\o(BC,\s\up6（→)）＝b，且a·b＞0，则△ABC是（)A．锐角三角形B．直角三角形C．钝角三角形D．等腰直角三角形5．设回归方程eq\o（y,\s\up6(^)）＝7－3x，当变量x增加两个单位时（）A．y平均增加3个单位B．y平均减少3个单位C．y平均增加6个单位D．y平均减少6个单位6．在如图所示的程序框图中，输入a＝eq\f(11π，6)，b＝eq\f(5π，3)，则输出c＝(）A．eq\f(\r(3）,3)B．eq\r（3）C．1D．07．观察数列1,2,2，3，3,3，4,4,4,4，…的特点，第100项为(）A．10B．14C．13D．1008．设△ABC的三边长分别为a，b，c,△ABC的面积为S，内切圆半径为r，则r＝eq\f（2S，a＋b＋c）；类比这个结论可知:四面体S－ABC的四个面的面积分别为S1，S2，S3，S4，内切球的半径为r,四面体S－ABC的体积为V,则r＝()A．eq\f(V,S1＋S2＋S3＋S4）B．eq\f（2V，S1＋S2＋S3＋S4）C．eq\f(3V,S1＋S2＋S3＋S4)D．eq\f(4V,S1＋S2＋S3＋S4）9．eq\b\lc\（\rc\）(\a\vs4\al\co1(\f(1＋i,1－i））)2014等于(）A．2iB．－1＋iC．1＋iD．－110．已知两条直线m，n，两个平面α，β.给出下面四个命题：①m∥n，m⊥αn⊥α；②α∥β,mα，nβm∥n；③m∥n,m∥αn∥α；④α∥β，m∥n，m⊥αn⊥β。其中正确命题的序号是(）A．①③B．②④C．①④D．②③11．已知f(x＋y）＝f（x）＋f(y）且f（1)＝2，则f(1）＋f（2）＋…＋f(n）不等于(）A．f（1）＋2f（1)＋…＋nf(1）B．feq\b\lc\［\rc\］（\a\vs4\al\co1（\f(nn＋1,2)）)C．n（n＋1）D．n（n＋1)f(1)12．如图是某汽车维修公司的维修点环形分布图．公司在年初分配给A，B，C，D四个维修点某种配件各50件,在使用前发现需将A，B，C，D四个维修点的这批配件分别调整为40,45,54,61件，但调整只能在相邻维修点之间进行．那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为()A．15B．16C．17D．18二、填空题(本大题共4小题，每小题4分，共16分)13．已知复数z＝eq\f(m＋i,1＋i)（m∈R,i是虚数单位）是纯虚数，则m的值是__________．14．按如图所示的程序框图运算,若输入x＝8，则输出k＝__________.15．观察下列式子1＋eq\f（1,22）＜eq\f(3，2）,1＋eq\f(1，22）＋eq\f(1，32)＜eq\f（5,3)，1＋eq\f(1，22)＋eq\f（1,32)＋eq\f（1,42）＜eq\f(7，4)，…，则可归纳出__________．16．已知x，y取值如下表：x014568y1.31。85.66.17。49。3从所得的数点图分析可知，y与x线性相关，且eq\o(y，\s\up6(^)）＝0。95x＋eq\o(a,\s\up6(^)），则eq\o(a,\s\up6（^）)的值为__________．三、解答题（本大题共6小题，共74分）17．(12分)调查某桑场采桑员和患桑毛虫皮炎病的情况，结果如下表：采桑不采桑总计患者人数1812健康人数578总计利用独立性检验估计“患桑毛虫皮炎病与采桑"是否有关，并求出认为两者有关系犯错误的概率是多少．(注：K2＝eq\f（nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d。P(K2≥k)0。0050.001k7.87910.828)18．(12分）已知x2－（3－2i）x－6i＝0,i为虚数单位．（1)若x∈R，求x的值;(2)若x∈C，求x的值．19．(12分）已知△ABC的三边长为a，b,c，且其中任意两边长均不相等．若eq\f(1,a），eq\f（1，b)，eq\f(1，c）成等差数列．（1）比较eq\r(\f（b,a))与eq\r(\f(c,b））的大小，并证明你的结论;（2）求证角B不可能是钝角．20．（12分)已知f(x)＝eq\f(bx＋1，ax＋12）eq\b\lc\(\rc\）(\a\vs4\al\co1（x≠－\f（1,a），a〉0))，且f(1)＝log162，f（－2)＝1。(1)求函数f(x）的表达式；(2）已知数列｛xn｝的项满足xn＝[1－f（1）］·［1－f(2）］·…·[1－f（n）］，试求x1，x2，x3，x4；(3)猜想{xn｝的通项．21．（12分）某市公交车票价按下列规则定价:(1)5公里以内(包括5公里），票价2元；(2)5公里以上，每增加5公里，票价增加1元(不足5公里按5公里计算)．已知相邻两个公共汽车站之间相距约1公里,如果沿途(包括起点站和终点站）共有16个汽车站，请设计一个算法求出某人坐车x公里所用的票价，画出程序框图．22．（14分）设△ABC的两个内角A，B所对的边分别为a，b,复数z1＝a＋bi,z2＝cosA＋icosB,若复数z1·z2为纯虚数，试判断△ABC的形状，并说明理由．

参考答案一、1．解析:复数z＝eq\f(z1，z2)＝eq\f（2＋i,1＋3i)＝eq\f(2＋i1－3i，1＋3i1－3i）＝eq\f(1,2)－eq\f（1，2)i，z对应的点的坐标为eq\b\lc\（\rc\)(\a\vs4\al\co1(\f（1,2)，－\f(1,2））)位于第四象限．答案：D2．解析：∵eq\f（1，2－i)＝eq\f（2＋i,2－i2＋i)＝eq\f（2＋i，5）＝eq\f(2，5)＋eq\f(1，5）i，∴eq\b\lc\｜\rc\｜(\a\vs4\al\co1(\f(1,2－i）))＝eq\r(\b\lc\(\rc\）(\a\vs4\al\co1(\f（2,5)))2＋\b\lc\(\rc\)（\a\vs4\al\co1(\f（1,5）)）2)＝eq\f(\r（5），5)。答案:B3．解析:A中球的体积与球的半径是函数关系，不是相关关系．B，C,D都正确．答案：A4．解析：由于a·b＞0，即|a｜|b|cos（π－∠ABC)＞0，即cos∠ABC＜0.又∵0＜∠ABC＜π，∴∠ABC是钝角．∴△ABC是钝角三角形．答案：C5．解析:由回归方程可知,y与x是负相关，x每增加2个单位,y平均减少6个单位．答案：D6．解析：由程序框图知，当输入a＝eq\f（11π,6),b＝eq\f(5π,3)时,tana＝－eq\f（\r（3),3），tanb＝－eq\r(3），则tana＞tanb．故输出c＝｜tana|＝eq\f(\r(3）,3）.答案：A7．解析：由于1有1个，2有2个，3有3个，…，则13有13个，所以1~13的总个数为eq\f(131＋13，2)＝91，故第100个数为14.答案：B8．解析：设四面体S－ABC的内切球球心为O，那么由VS－ABC＝VO－ABC＋VO－SAB＋VO－SAC＋VO－SBC，即V＝eq\f（1,3）S1r＋eq\f（1，3)S2r＋eq\f（1，3）S3r＋eq\f(1，3)S4r，可得r＝eq\f(3V，S1＋S2＋S3＋S4）。答案：C9．解析：∵eq\f(1＋i,1－i)＝eq\f（1＋i2，2)＝eq\f(2i,2）＝i,∴eq\b\lc\(\rc\）(\a\vs4\al\co1（\f（1＋i,1－i))）2014＝i2014＝(i2）1007＝－1。答案：D10．解析：由α∥β,mα，nβm∥n或m，n异面，∴②错；由m∥n，m∥αn∥α或nα，∴③错．故选C.答案：C11．解析：由f（x＋y）＝f（x）＋f（y）且f(1)＝2,知f（2)＝f(1)＋f(1)＝2f(1),f(3)＝f(2)＋f(1)＝3f(1），…，f(n)＝nf(1)，∴f(1）＋f（2)＋…＋f(n)＝(1＋2＋…＋n）f(1)＝eq\f(nn＋1，2）f(1）＝n（n＋1)．答案：D12．解析：方法一：若AB之间不相互调动，则A调出10件给D，B调出5件给C,C再调出1件给D，即可满足调动要求，此时共调动的件次n＝10＋5＋1＝16；若AB之间相互调动，则B调动4件给C，调动1件给A,A调动11件给D，此时共调动的件次n＝4＋1＋11＝16。所以最少调动的件次为16，故应选B。方法二:设A调动x件给D（0≤x≤10)，则调动了(10－x)件给B，从B调动了5＋10－x＝(15－x）件给C，C调动出了15－x－4＝(11－x）件给D,由此满足调动需求，此时调动件次n＝x＋(10－x）＋（15－x)＋（11－x）＝36－2x，当且仅当x＝10时，n取得最小值16，故应选B。答案：B二、13．解析:z＝eq\f（m＋i，1＋i)＝eq\f(m＋i1－i,2)＝eq\f（m＋1，2)＋eq\f（1－mi,2），∴eq\f(m＋1，2)＝0，且eq\f(1－m，2)≠0.∴m＝－1。答案：－114．解析：输入x＝8时，k＝0，第一次循环,x＝2×8＋1＝17，k＝1，x＜115；第二次循环，x＝2×17＋1＝35,k＝2，x＜115；第三次循环，x＝2×35＋1＝71,k＝3,x＜115；第四次循环,x＝2×71＋1＝143，k＝4，x＞115，输出x＝143,k＝4.答案：415．解析：根据三个式子的规律特点进行归纳可知，1＋eq\f(1,22)＋eq\f(1，32）＋eq\f（1，42）＋…＋eq\f(1，n＋12）＜eq\f(2n＋1，n＋1）(n∈N＊)．答案：1＋eq\f（1，22)＋eq\f（1，32）＋eq\f（1,42）＋…＋eq\f(1,n＋12)＜eq\f(2n＋1,n＋1)(n∈N＊)16．解析：eq\x\to(x)＝eq\f（1,6)×(0＋1＋4＋5＋6＋8)＝4，eq\x\to（y）＝eq\f(1,6)×(1。3＋1.8＋5.6＋6。1＋7。4＋9。3)＝5。25，又eq\o(y,\s\up6（^))＝0。95x＋eq\o（a，\s\up6（^))必过样本中心点（eq\x\to(x)，eq\x\to（y）)，即(4,5.25)，于是有5.25＝0。95×4＋a，解得a＝1。45。答案：1。45三、17．解：因为a＝18，b＝12，c＝5，d＝78,所以a＋b＝30,c＋d＝83,a＋c＝23，b＋d＝90，n＝113，所以K2的观测值k＝eq\f(nad－bc2，a＋bc＋da＋cb＋d）＝eq\f(11318×78－5×122，30×83×23×90）≈39。6＞10。828。所以有99。9%的把握认为“患桑毛虫皮炎病与采桑”有关系，认为两者有关系会犯错误的概率是0.1％。18．分析：（1)利用复数相等的充要条件可直接求解；（2）中要求x的值，就应先设出x的代数形式再利用复数相等的充要条件求解．解：（1）当x∈R时，由已知方程，得(x2－3x)＋(2x－6）i＝0，则eq\b\lc\{\rc\(\a\vs4\al\co1(x2－3x＝0,,2x－6＝0，)）解得x＝3.(2）当x∈C时,设x＝a＋bi（a，b∈R）,将其代入已知方程，整理,得(a2－b2－3a－2b)＋（2ab－3b＋2a－6）i＝0。则eq\b\lc\｛\rc\（\a\vs4\al\co1(a2－b2－3a－2b＝0，,2ab－3b＋2a－6＝0，））解得eq\b\lc\{\rc\（\a\vs4\al\co1（a＝0，,b＝－2))或eq\b\lc\｛\rc\（\a\vs4\al\co1（a＝3，,b＝0。)）故x＝－2i或x＝3.19．（1)解：大小关系为eq\r（\f（b，a))＜eq\r（\f（c，b）).证明如下:要证eq\r（\f(b,a））＜eq\r（\f（c,b）），只需证eq\f(b，a）＜eq\f(c，b）。∵a,b，c＞0，∴只需证b2＜ac.∵eq\f（1，a)，eq\f(1，b),eq\f（1，c）成等差数列，∴eq\f（2,b)＝eq\f（1,a)＋eq\f(1,c)≥2eq\r（\f(1，ac））。∴b2≤ac。又△ABC的任意两边长均不相等，即a，b，c任意两数不相等,∴b2＜ac成立．故所得大小关系正确,即eq\r(\f(b，a））＜eq\r（\f(c,b)）。(2)证明：假设角B是钝角,则cosB＜0,而cosB＝eq\f（a2＋c2－b2,2ac)≥eq\f（2ac－b2，2ac)＞eq\f(ac－b2，2ac）＞0。这与cosB＜0矛盾，故假设不成立，即角B不可能是钝角．20．解：(1)把f(1）＝log162＝eq\f（1,4)，f(－2）＝1代入f(x）＝eq\f（bx＋1，ax＋12)，得eq\b\lc\{\rc\(\a\vs4\al\co1（\f（b＋1,a＋12）＝\f（1,4)，,\f(－2b＋1，1－2a2)＝1，））整理,得eq\b\lc\{\rc\（\a\vs4\al\co1（4b＋4＝a2＋2a＋1，,－2b＋1＝4a2－4a＋1,）)解得eq\b\lc\{\rc\(\a\vs4\al\co1（a＝1,,b＝0，）)所以f（x)＝eq\f(1,x＋12)（x≠－1)．(2)x1＝1－f(1）＝1－eq\f（1，4）＝eq\f（3，4)，x2＝eq\f（3,4）×eq\b\lc\（\rc\）(\a\vs4\al\co1（1－\f（1,9)）)＝eq\f(2，3)，x3＝eq\f(2,3)×eq\b\lc\(\rc\）(\a\vs4\al\co1(1－\f(1，16))）＝eq\f(5,8），x4＝eq\f（5,8)×eq\b\lc\（\rc\）(\a\vs4\al\co1(1－\f(1,25)))＝