人教A版选择性必修第一册：第一章 空间向量与立体几何 单元检测卷（学生版+解析版）

第一章空间向量与立体几何单元检测卷（难）

一、单选题.

1.（2。21•全国高二课时练习）若向量而垂直于向量2和人向量3=笳+〃B（九〃£区）且/1,〃工0,贝1」（）

A.m//nB.mLn

而不平行于入前也不垂直于3以上三种情况都有可能

C.D.A

2.（2020•江苏省姜堰第二中学高二月考）如图，在正方体488-AgGA中，点”，N分别

A

是面对角线A3.与4仅的中点，若次=£DC=b>西=入则丽=（）

以・

B.g（a+坂-c）1

.2

3.（2021•江苏高二期末）在棱长为1的正方体ABC。-A8GA中，M、N分别是人蜴、人儿的中点，则

直线A”与。N所成角。的余弦值为（

A1R2「后、2娓

5555

4.（2021•湖北荆州•高二期末）如图，在三棱柱ABC-A8IG中，8G与瓦。相交于点

O,=^A.AC=ZBAC=60,AA=3,AB=AC=2,则线段40的长度为（）

回V295后

A.DR.---Cr.-U.------

2222

5.（2020•浙江温州市•温州中学高三月考）如图四边形A3C£>,AB=BD=DA=2,8。=CO=&.现将△ABO

沿8。折起，当二面角A-即-。处于々空过程中，直线AB与CO所成角的余弦值取值范围

OO

是（）

5应万夜5x/2

B.'T'~

叵。邛

VD.

6.（2021•北京高一期末）在棱长为1的正方体458-44£口中，M,N分别为44，CC,

的中点，O为底面48co的中心，点尸在正方体的表面上运动，且满足NP_LMO,则下列说

法正确的是（）

A.点?可以是棱的中点B.线段NP的最大值为立

2

C.点P的轨迹是平行四边形D.点P轨迹的长度为1+&

7.（2021•河北饶阳中学高三其他模拟）如图，正方体A3CO-4qGR的楂长为6,

点尸是棱AA的中点，AC与8。的交点为。，点M在棱8C上，且BM=2MC,

动点T（不同于点M）在四边形ABCO内部及其边界上运动，且7Ml.OQ,则直

线4户与7M所成角的余弦值为（）

亚RV106n45

A.-------D.-------C.------U.--

4545

8.（2022•全国高三专题练习）在棱长为1的正方体4BCO-A与GA中，尸是线段BG上的点，过的平面

。与直线PD垂直，当尸在线段8G上运动时，平面。截正方体ABC。-A8CA所得的截面面积的最小值

是（）

A.1B.-C.近D.&

42

二、多选题.

9.（2020•辽宁高二期中）给出下列命题，其中为假命题的是（）•

A.已知方为平面。的一个法向量，比为直线/的一个方向向量，若万J■所，则"3

B.已知日为平面。的一个法向量，比为直线/的一个方向向量，若（爪所”,，则/与。所成角为1

C.若三个向量6,己两两共面，则向量Q,B,乙共面

D.已知空间的三个向量入5,c,则对于空间的任意一个向量户，总存在实数x，y，z使得防+Z5

10.（2021•邵阳市第二中学高三月考）如图，菱形A8CD边长为2,Zfi4D=60°,E为边A8的中点.将“IDE

沿OE折起，使A到且平面AOE_L平面8COE,连接A8,AC.

则下列结论中正确的是（）•

A.BD1ACB.四面体A'CDE的外接球表面积为87r

C.叱与AO所成角的余弦值为?D.直线A8与平面AC。所成角的正弦值为远

4

11.（2021•重庆南开中学高三其他模拟）设所有空间向量的集合为U=｛（N，W，X3）W，W，&eR｝，若非空集

合满足：①V无peM,x+y^M,@VaeR,xeA/,axeM,则称M为a的一个向量次空间，

已知A,。均为向量次空间，则下列说法错误的是（）

A.=0

B.AIJ5为向量次空间

C.若人土8,则8=*

D.若8工｛0｝,则依wA,总于£8且尹。，使得了j=O

12.（2021•辽宁）已知直四棱柱4BCO-AB|GR,底面ABCD为矩形，AB=2,BC=6,侧棱长为3,

设P为侧面所在平面内且与。不重合的任意一点，则直线8。与直线P。所成角的余弦值可能为（）

A.--B.；C.—D.-

2228

三、填空题.

13.（2020.全国高二课时练习）已知向=13,W=19,B+闻=24,则归一传.

14.（2021•浙江）如图，在棱长为4的正方体ABCO-AgG。中，M是棱4A上的动点，/V是棱8c的中

点.当平面与底面48co所成的锐二面角最小时，AM=.

15.（2021•安徽高二期末（理））已知正四面体A-88的外接球半径为3,MN为其外接球的•条直径，

尸为正四面体A-BCO表面上任意一点，则丽.两的最小值为.

16.（2021•全国高三其他模拟）在棱长为3的正方体48C。-A4GA中，BE=2EC，点P在正方体的表

面上移动，且满足87_LAE,当尸在CG上时，k"=；满足条件的所有点尸构成的平面图形的周长

为.

四、解答题.

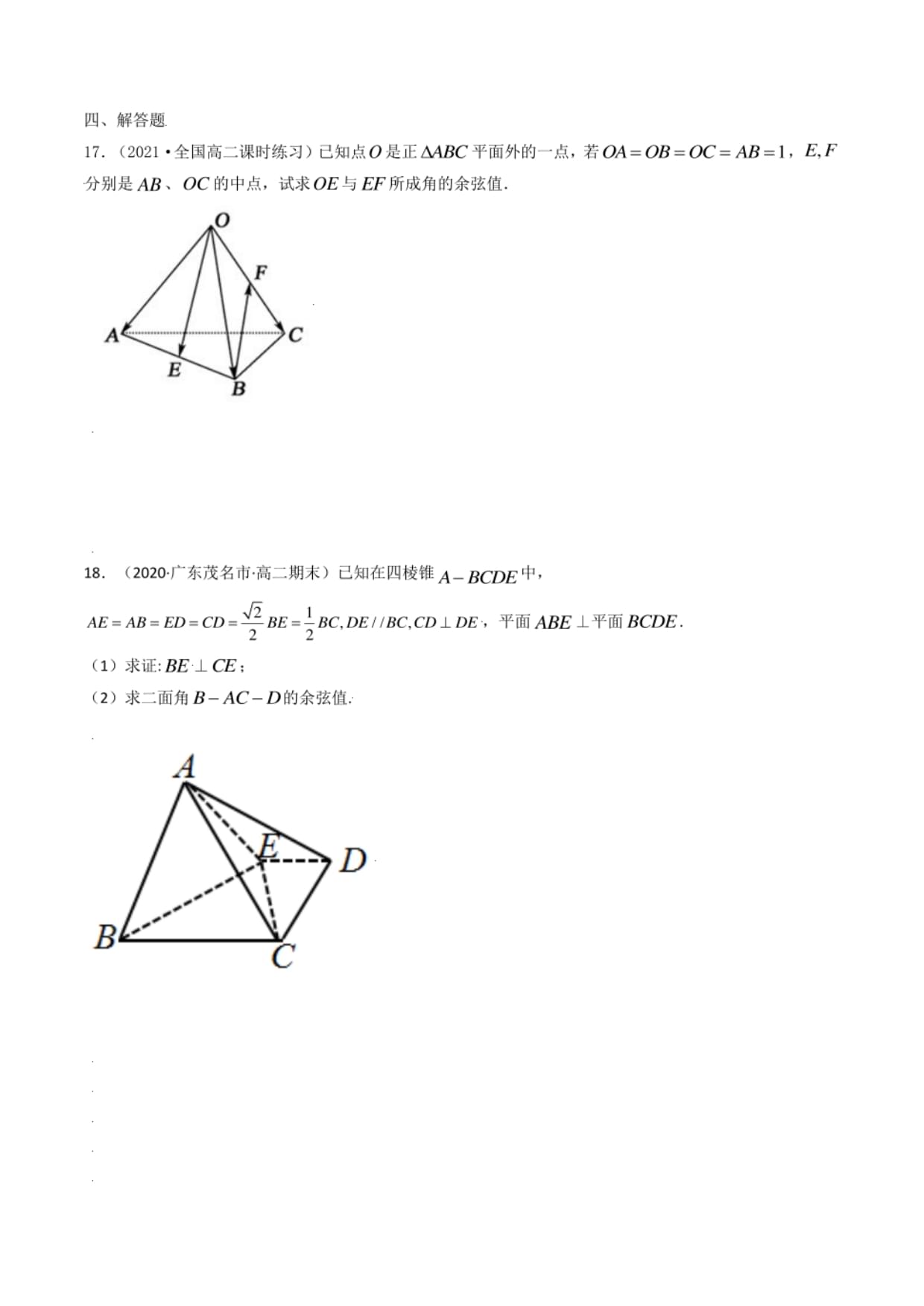
17.（2021•全国高二课时练习）已知点。是正AA3C平面外的一点，若。4=OB=OC=A8=1,E,F

分别是48、OC的中点，试求OE•与所所成角的余弦值.

18.（2020•广东茂名市•高二期末）已知在四棱锥A-BCDE中，

AE=AB=ED=CD=—BE=-BC,DE//BC,CD±DE,平面ABE_L平面BCDE.

22

（1）求证:BE_LCE；

（2）求二面角8—AC—。的余弦值.

D

Bk

C

19.(2021•江苏省涕水高级中学高二月考)如图，四棱锥P-ABC。中，底面A3CD为矩形，PA_L平面A8CO,

E是尸。的中点，过作平面8C所交平面?A0于所.

(1)证明：F是弘的中点；

=也,求三棱锥E-48的体积.

(2)设二面角力一AE-C为60°,AP=\tAD

BC

20.(2021•江苏省新海高级中学高二月考)如图1,在等边△A8C中，点。、E分别为边AAAC上的动点

DF

且满足DEH8C,记==2.将△4)E沿£>£翻折到△MDE的位置并使得平面"力七_1_平面DECB，连接MB,

BC

MC得到图2,点N为MC的中点.

(1)当EN〃平面M8O时，求义的值;

(2)试探究：随着4值的变化，二面角5-MD-E的大小是否改变？如果改变，请求出实数2与二面角平

面角的正弦值的函数关系：如果不改变，请求出二面角4-例。-£■的正弦值大小.

21.（2021•河南高二期末（理））如图，四棱锥中，底面4BCO为正方形，△R48为等边三角

形，平面底面ABC0,E为AO的中点.

（1）求证：CE工PD；

（2）在线段8。（不包括端点）上是否存在点尸，使直线赫与平面尸所所成角的正弦值为手，若存在,

确定点尸的位置；若不存在，请说明理由.

22.（2021・重庆巴蜀中学）如图，在三棱台ABC-agG中，底面AAHC是边长为2的正三角形，侧面ACGA

为等腰梯形，且AG=A4,=1,。为AG的中点.

（1）证明：AC±BD-

（2）记二面角A。-8的大小为夕，8Gpy时，求直线人凡与平面所成角的正弦值的取值

范围.

Ci

第一章空间向量与立体几何单元检测卷（难）

一、单选题

1.（2021,全国高二课时练习）若向量而垂直于向量£和后，向量3=/1£+〃5（/1,〃€尺）且

4,〃工0,则（）

A.m//nB.tnLn

c.记不平行于G，石也不垂直于GD.以上三种情况都有可

能

【答案】B

【详解】

向量zn垂直于向量a和另，则加・a=0,加»=0，

又向量〃=2a+〃坂，

所以W?•〃=机•（4。+jub）=Xm-a+•力=0,

所以机_L〃.

故选：B.

2.（2020•江苏省姜堰第二中学高二月考）如图，在正方体ABCO-AMGA中，点M,

分别是面对角线AB与6Q的中点，若丽=£,~DC=by西=入则丽=（）

A.#+=）B.如+C.茅一工）D.1（c-a）

【答案】D

【详解】

因为点M，N分别是面对角线4B与8a的中点，万5=£,DC=b，DD^=c,

所以MN=M*+BB；+BN

=第十西丽

=3⑷+砌+西+g阿+珂

=知+小）+;（—力）

故选:D.

3.（2021•江苏高二期末）在棱长为1的正方体中，加、N分别是AA、AA

的中点，则直线AM与ON所成凭。的余弦值为（）

1

2756

A.5-

以点A为坐标原点，AB.AD.AA所在直线分别为X、y、z轴建立空间宜角坐标系,

加（触），丽=（。,0，8S＜海而，儡蠲二祗

2X2

2

因此，直线与ON所成角。的余弦值为:，

故选：B.

4.（2021•湖北荆州•高二期末）如图，在三棱柱4BC-A8C中，与8。相交于点

0,/AA8=/AAC=/8AC=60，AA=3,48=AC=2,则线段AO的长度为（）

回回5后

A.-----D.------C.-U.-----

2222

【答案】A

【详解】

依题意得|胡卜3,|同=,4=2,福•丽=福.配=3,ABAC=2

所以

=AO=-(AA+AC+AB)2=-(AA^+AC2+AB2+2X\AC+2AA^AB+2ACA§

故补孚

故选：A.

5.（2020•浙江温州市•温州中学高三月考）如图四边形A8CO,AB=BD=DA=2,

8C=CO=亚.现将△A3。沿80折起，当二面角A—BO—C处于三字过程中，直线4B

与CO所成角的余弦值取值范围是（）

5>/2y/2~\f>/25&

A.-----B.—

8888

邛用,陷B

【答案】D

【详解】

在四边形A8co中，连接AC交8。「点0,如下图所示：

AB=BD=DA=2,BC=CD=6，又因为4C=AC,:.^ABC^ADC,

所以，ZBAC=ZDAC,故AC_LB7),即AO_L8£>,CO±BD,

且AC==G，CO=4BC2-BOr=b

翻折后，对应地，BD1AO,BDtCO,\AOr\CO=O,所以，8D_L平面ACO,

45不

二面角4一班)一。的平面角为NA。。，设NAOC=6,则,

以点。为坐标原点，oc、0。所在直线分别为X、y轴建立如下图所示的空间直角坐标系,

A

则点A(68se,0,6sine)、B(0-1,0),C(l,0,0),D(0J,0),

所以，AB=(-73cos6>,-1,-V3sin6>),CD=(-l,l,0),

8s〈丽丽>=雪名=叵泻5>/2&

画网2夜

■sO

所以，|cos<AB,CD>|e0,士

8

因此，直线AB与所成角的余弦值取值范围是卜竽］

故选：D.

6.（2021•北京高一期末）在棱长为1的正方体ABC。-中，M,N分别为A4,

C。的中点，。为底面ABCD的中心，点P在正方体的表面上运动，且满足NP工MO,

则下列说法正确的是（）

B.线段N尸的最大值为史

A.点尸可以是棱的中点

2

C.点P的轨迹是平行四边形D.点P轨迹的长度为1+五

【答案】B

【详解】

在正方体A8CO-ABCA中，以点O为坐标原点，分别以D4、DC、。仅方向为X轴、y

轴、Z轴正方向，建立空间直角坐标系,

B

因为该正方体的棱长为1,",N分别为A4,CG的中点,

则£＞（0,0,0）,A/h,o,H,

所以西=6,-；,；），设p（x,yz）,则而=卜,y-

因为NPLMO,所以而•丽=0

所以**-1）+如一£|=0,即2x-2y+2z=T,

令z=0,当x=g时，y=l；当/=0时，y=g；

取小；,1,0）,尸（o,g,o）,

连接M,FN,NE,则丽=（—；,—g,0）,丽=（一/0,£）,

贝I」乔•丽=_U+（_g）x（_g）+Oxg=O,

E/VOA?=--xi+Ox|—|+-!-x-!-=0,

22\2）22

所以所_LOM,EN1OM,

又EFcEN=E,且Mu平面EEN,ENu平亚EFN,

所以OM_L平面EFN,

所以，为使NPLOM,必有点Pe平面EFN,又点P在正方体的表面上运动，

所以点尸的轨迹为正三角形EFN,故C错误；

因此点尸不可能是棱8瓦的中点，故A错误；

线段稗的最大值为N尸-也，故B正确：

2

点产筑迹的长度为立+走+也=逑，故D错误：

2222

故选：B

7.（2021•河北饶阳中学高三其他模拟）如图，正方体A8CO-ABCQ的棱长为6,点尸是

棱AA的中点，AC与5£＞的交点为。，点M在棱BC上，且BM=2MC,动点7（不同

于点在四边形A3CD内部及其边界.上运动，且7M_LO/，则直线用尸与

7M所成角的余弦值为（）

A.®B.®C.@D.正

4545

【答案】B

法一：易知BOJLAC.

因为A尸J•平面4BCD,所以A尸！80，所以801平面4F0,

又OFu平面AF。，所以5。_1_。尸，

在棱0C上取一点M且DN=2NC,连接A/M,则NM〃8。，所以NWJ_OF,所以动点了

的轨迹为线段MN（不包括M）.

取棱CG的中点从连接DH,易知DH/FB',则即异面直线8厂与7M所成的角.连

接BH,因为而三孕=3不，BD=6yf2>BH=3亚，

所以8，/m用=空卫吐空=回

2DHxBD5

法二：以人为坐标原点，直线4），A8，M分别为x,y,z轴建立如图所示的空间直角坐标

系，

易知4(0,6,6),尸(0,0,3),M(4,6,0),53,3,0),设T(x,y,O),则扁=(4-*,6-y,0)，

4%=(0,-6,-3)，苏=(-3,-3,3)

由题意知前.办=一3(4-x)_3(6_y)=0，得丫=1。一工，

所以笳=(47,…,0)，则H上回H际X募望+(1)2'

又了不与点M重合，所以工-4=0,所以cos,/7,俞),

所以直线B7与TM所成角的余弦值为学，

故选：B.

8.（2022•全国高三专题练习）在棱长为1的正方体ABCO-ABCR中，尸是线段上的

点，过A的平面。与直线PD垂直，当尸在线段BG上运动时，平面a截正方体

ABCD-ABCQ所得的截面面积的最小值是（）

A.1B.-C.—D.y/2

42

【答案】C

讨论，确定截面a与各棱的交点，求出截面面积关于，的表达式，由此可解得截面面积的最

小值.

【详解】

以点A为坐标原点，AB、AD.AA所在直线分别为X、丁、z轴建立如下图所示的空间直

角坐标系，

则A(0,0,0)、A(0,0,1)、3(1,0,0)、4(1,0,1)、C(l,l,0)、G(1,1,1)、D(o,l,o)、D,(0,1,1),

设点其中OSTI.

①当，=0时，点P与点5重合，55=(-1,1,0),AC=(1,1,O),鬲=(0,0,1),

所以，BDAC=0,而・丽=0,则3O_LAC,1AAt,

・.・ACc/U1=A,平面"1clC,此时平面。即为平面例GO,

截面面积为S=A4)•AC=>/2；

②当r=l时，同①可知截面面积为s=&：

③当0<zvl时，而=AS=(1,1,-1),

­.DP^C=l+r-l-/=O,：.A.C1PD,则ACua,

设平面a交棱DR于点E(OJz),CE=(-l,0,z),

DPCE=-\+tz=Of可得z」＞l,不合乎题意.

t

设平面。交棱A4于点”(x,0,0),CM=(x-l,-l,O),

DPCA7=X-1-(/-1)=0,可得X=/,合乎题意，即M(1,0,0),

同理可知，平面。交棱GA于点N(1TJ1),

丽二(1T,1,O)=祝，且AN与MC不重合，故四边形AMCN为平行四边形,

■■.KrAC,A2-t

AC=(U,T),AN=(1H。)，8SW二祠同石j»+2.

代T+l)

则sinZCAjN=0-cos2Z.C\N

，3任-2f+2)

所以，截面面积为

S=2s小“=|桐•|纲sin/CAN=J2rT+l)=}+：邛〈技

综上所述，截面面积的最小值为迈.

2

故选：C.

二、多选题

9.(2020•辽宁高二期中)给出下列命题，其中为假命题的是()

A.已知”为平面。的一个法向量，比为直线/的一个方向向量，若无JL比，则///a

B.已知日为平面。的一个法向量，所为直线/的一个方向向量，若低昉=4，则/与a所

成角为?

O

C.若三个向量b，［两两共面，则向量万，b»［共面

D.已知空间的三个向量不，5,3,则对于空间的任意一个向量广，总存在实数x，y，z使得

p=xa+yb+zc

【答案】ACD

【详解】

对于A：由题意可得或/ua,故A错误；

对于B：

由图象可得，ZCAD=y,则ND48=《,

所以乙4。8=[,根据线面角的定义可得：/与。所成角为I，故B正确

对于C：若三个向量2,b»-两两共面，但三个向量不一定共面，故C错误：

对于D：当空间的三个向量a,5,e不共面时，对于空间的任意一个向量P,总存在实数

%y，z使得力=储+y5+zd,故D错误.

故选：ACD

10.（2021•邵阳市第二中学高三月考）如图，菱形A8CD边长为2,/丛。=60。，E为边A8

的中点.将“1D石沿0E折起，使A到4,且平面ADE_L平面8CQE,连接48,A!C.

则下列结论中正确的是（）

A.BD1AVB.四面体4CDE的外接球表面积为配

C.8C与AO所成角的余弦值为。D.直线48与平面ACD所成角的正弦值为

76

4

【答案】BCD

【详解】

由题知，为正三角形，DELAB,将“IDE沿DE折起，使A到H,且平面平

面BCDE,则EB,ED,ET两两垂直，以£点坐标原点，建立如图所示空间直角坐标系，

z

对于A,8(1,0,0)，0(0,75,0),4(0,0,1),C(2,G,0),fib=(-1,75,0)»4七=(2,石,一1)，

贝I」访.A；C=-2+3=]wO,故8。与A，C不垂直，故A错误；

对于B,取C£的中点F,联结OF,又DE上DC,

则FE=FD=FC=LcE=Lj3+4=4，

222

过F作「O_L平面COE,四面体40的外接球球心。在FO上，作OW_LAE,

设。b=x,OD=OA'=R,在R&0FD,中，

W7?2=(^y-)2+X2=(^y-)2+(1-X)2,解得X=；,R=&,

故四面体ACDE的外接球表面枳为4划?2=8万,故B正确；

对于C，5C=(1,75,0)*A%=(0,石,-1),设8C与4。所成角为。,

BC^D

则cos6=r----=——=-t故c正确；

BC-A'D2X24

对于D,A78=(l,0,-l)，丘=(2,石,-1)，A\C)=(0,>/3,-l)»

设平面48的法向量;;=(x,y,z)

n-A'C=2x+>/3y-z=0

取2=G,

n-A'D=Gy-z=0

贝/；=(o,i,V5)，

T->

­，，A*R、­

则vUo&",r\oT2x&一丁，

nA'B\

故直线A'5与平面4'CO所成角的正弦值为亚，D正确;

4

故选：BCD

11.（2021•重庆南开中学高三其他模拟）设所有空间向量的集合为

〃3=｛（5,生玉）即工2,&£q，若非空集合Mq*满足：①V元ywM,x+yeM,②

V.wR,XGM,或eM,则称M为N的一个向量次空间，已知A,8均为向量次空间，

则下列说法错误的是（）

A.AcB/0

B.AUB为向量次空间

C.若A=8,则8=*

D.若8/｛0｝,则依eA,总学€8且了工。，使得元4=0

【答案】BCD

【详解】

若M为"的•个向量次空间，则由②X/awR.xeM,而wM可知，OeAf»

再结合①可得向量次空间包含元素（0,0,0）

所以向量次空间所包含的元素对应的点为穿过空间坐标系原点的一条直线，

或者经过空间坐标系原点的一个平面，或者是整个空间.

对于A,显然当A,8均为向量次空间时，｛（0,0,0）｝qAcB,所以A正确；

对于B,当A,“分别为空间中经过原点的两条不同的直线时，取元eA,且无了不为

（0,0,0）,

则元不符合①，所以B错误：.

对于C,例如A对应一条过原点的直线/,8对应一个过直线/的平面时，满足Aub,

但BwR"C错误；

对于D,当A,8分别对应空间中两条过了原点，但是不相互垂直的直线时，不成立，D错

误.

故选：BCD

12.（2021•辽宁）已知直四棱柱ABS-AMGA,底面ABCO为矩形，AB=2,BC=6,

侧棱长为3,设尸为侧面明。口所在平面内且与。不重合的任意一点，则直线与直线

尸。所成角的余弦值可能为（）

A.--B.JC.—D.：

2228

【答案】BC

【详解】

以。为原点，D4、DC、。2所在直线分别为x、y、z轴建立空间直角坐标系如图，则

B(>/3,2,0),.(0,0,3),则西=卜疯-2,3),设点P(x,O,z),则丽=(x,O,z).

设直线BA与直线PD所成的角为e,则

8E网I/叫—.—叫Al=扁\BD\画DP\=易|-\/3x+3？z|

令x=rcosa,z=rsina,其中r>0,

则8s6」dsa+35a|』sina一代。sa|=母/_去"

4r42\6)2

所以，COS0W0,^~.显然，gce'

故选：BC

三、填空题

13.（2020•全国高二课时练习）已知同=13,忖=19,归+可=24,则**

【答案】22

【详解】

因为k+Z?|=a-\-2ab+b'=#+£/+1『=132+2"+9=24、

所以2：•1=46,

2r2rrr

H=a-2ab+b2=132—46+9=484,

故卜-*22.

故答案为：22

14.（2021•浙江）如图，在棱长为4的正方体4BCQ-AB|GR中，M是棱上的动点,

N是楼BC的中点.当平面与底面A8CO所成的锐二面角最小时，.

设M(4,0,a)(0<a<4),N(2,4,0),.(0,0,4)

MN=(-2,4,-a),丽=(2,4,-4)

设平面的一个法向量为7=(x,y,z)

(4-d)z

n-MN=0J-2x+4)，-az=04

n-I^N=0=>\2x+4y-4z=0

(a+4)z

令z=8,x=8-20y=a+4,则〃=(8-勿,a+4,8)

平面ABC。的法向量的一个法向量为砥=(0,0,1)

设平面RMN与底面A8CO所成的锐二面角为。

________88

所以cos6=

mJ(8-2不+(a+4)2j5/-24a+144

24128

当。=正=《时'cos。有最大，则8有最小，所以

Q

故答案为：］

15.(2021•安徽高二期末(理))已知正四面体A-BCD的外接球半径为3,MV为其外

接球的一条直径，P为正四面体A-8CO表面上任意一点，则丽••丽的最小值为

【答案】-8

【详解】

设正四面体外接球球心为O,

正四面体A-BCD的外接球半径为3,

设正四面体A-3C。内切球半径为，一个面的面积为S,高为〃，则%m=4xgsr=gs/z,

所以〃=4r,显然r+3=〃=4r,所以r=l,即归。而“=1.

^-PN=(PO+OM)(Pd+ON)=PO+OMON=PO-9A-9=-^

故答案为：-8.

16.(2021•全国高三其他模拟)在棱长为3的正方体"CD-ABCQI中，瓦=2反，点P

在正方体的表面上移动，且满足4P_L〃E,当尸在CG上时，|"|=;满足条件的所

有点尸构成的平面图形的周长为.

【答案】V225a+2M

【详解】

如图，取CG、8上的点分别为N、M，连接AM、MN、B、N、ABit使得ABJ/MN,

「.A、B、、N、M四点共面，且四边形4qNM为梯形.

•.・正方体ABC。—AMGA的边长为3,

所以，以。为坐标原点，D4所在直线为“轴，OC所在直线为》轴，OR所在直线为z轴

建立如下图所示的空间直角坐标系，

则4(3,0,0)、4(333)、.(0,0,3)、E(l,3,0).

设点M(0,犯0)、N(0,3,〃)，设点E_L4”,且扉=(1,3,-3),丽=(-3,小0),

印•丽？=-3+3m=0,解得机=1,

•••丽=(0,3,3),^EA^*=9-9=0,：.D.E±ABit

由AMP)A同=A,则。或_1平面48~知.

•••点尸在正方体表面上移动，且AP_L〃E,则点尸的运动轨迹为梯形44NM.

丽二(0,2,〃)，席•丽=6-3〃=0,解得〃=2,即点N(0,3,2).

所以，当P在CG上运动时，MH=|训=J(3-0『+(0-3)2+(0-2)2=后,

又Q|NM|=2日,|A印=3人，|AM=[4M=M，

所以，梯形为等腰梯形，

且梯形ABNM的周长卜周+|朋时+2kM=3应+2应+2而=5立+2而.

故答案为：夜；5夜+2，石.

四、解答题

17.(2021•全国高二课时练习)已知点。是正AABC平面外的一点，若

OA=OB=OC=AB=\,瓦户分别是AB、OC的中点，试求OE与所成角的余弦

值.

n

【答案】|2

【详解】

i^OA=a,OB=b,OC=c,!lIiJa-S=S-c=c-a=-i,|a|=|^|=|c|=l,

OE=^a+b）fBF=^c-b,

丽.丽=；8+与｛；）一@=；（＜72+；尻£一£石一万2）

111——Ir--r0

=——ac+—bc-ab-b

2（22）

2

所以8s〈配叫=黄赢=逅叁=3，

2X2

因为异面直线成角的范围是(0段，所以异面直线。£与8F所成角的余弦值大于等于0,

故异面直线OE与BF所成角的余弦值为:.

18.(2020•广东茂名市•高二期末)已知在四棱锥人_BCDE中，

AE=AB=ED=CD=-BE=-BC,DE//BC.CD1DE，平面ABE，平面BCDE.

22

D

(1)求证:BE_LCE；

(2)求二面角8—AC-O的余弦值.

【答案】(1)证明见解析；(2)-画.

11

【详解】

(1)证明：CD±DE^EDC=90MCE2=ED2+CD2

ED=CD=-BE=-BC

22

CE2+BE2=ED2+CD2+BE2

2

=^cj+(lScp^Bcp^

故BE工CE.

又•「面ABEJ_平面BCDE,且面ABE(］面BCDE=BE

CE_L面A8E

又8EU面ABE,:.BE±CE.

(2)取8E的中点。，连49,则AO_LBE,从而40JL面8CDE.

取。为原点，为z轴，过。且平行于CD的直线为x轴，过。平行于8c的直线为y轴,

建立如图空间直角坐标系.

设4B=2,则8(1,-1,0),C(1,3,0),D(-1,3,0),4(0,0,

CD=(-2,0,0),C4=(-1,-3,⑶，通=-扬,BC=(0,4,0)

设平面ACD的法向量为%=（%,如z.）,

瘀:磬五。，令马二日得还传，闾

演CA=0[-X1-3y（+y2z,=0k3）

设平面ABC的法向量为质=（9,必/2）

n,AB=QX,-J2-yf2z2=0

则——a即《

n,BC=04y2=0

令z?=后，得利=（2,0,夜）

一一如•/0+0+2二底

/.COS<%%>=―!~i―T

’1国1•同~ir

2X>/F+0+2

。+1+

又由图知二面角B-AC-D为钝角

二面角B-AC-D的余弦值为一亘

11

19.（2021•江苏省滦水高级中学高二月考）如图，四棱锥P-中，底面A38为矩形,

E4_L平面48CO,E是尸。的中点，过BC作平面8C£尸交平面PAO于四.

（1）证明：尸是RA的中点;

（2）设二面角力一AE-C为60。，AP=\,AD=6,求三棱锥七一ACD的体积.

【答案】（1）证明见解析；（2）在

8

【详解】

解：（1）证明•.•四棱锥P-ABCD中，底面488为矩形，

BC//AD,

•.•8C仁平面24£）,ADu平面上位），

5C〃平面PA0,

•••过BC作平面BCEF交平面PAO于EF.

」.EFu平面E4O,且EF//BC,

:.EFMAD,

•.•E是的中点，.•.尸是P4的中点；

（2）以A为原点,AB为x轴，AO为N轴，”为z轴，建立空间直角坐标系,

设A8=f,r>0,则40,0,0).C(f,石，0),。(0,6，0),E((),与,1),

AE=(0,与,；),AC=(/,60),AD=(0,日0),

平面ADE的法向量及=（1,0,0）,

设平面ACE的法向量而=（x,y,z）,

in-AC=tx+>/3y=0

则__JJ1，取y=i,得所=(—-»i»-x/3)

in-AE=——y+—z=01

22

•・•二面角。-AE-C为60。,

3。=得篇=六4由”＞。，解得遍，［54

54cO=-x^x-=—

JCD224

E到平面ACD的距离d=gPA=g,

*'-三棱锥E-ACD的体积VE_ACD=；xS”xd=gX乎x1=^.

20.（2021•江苏省新海高级中学高二月考）如图1,在等边△ABC中，点。、E分别为边

DF

AB、AC上的动点且满足。石〃AC,记力:二丸.将△AOE沿OE翻折到△的位置并使得

BC

平面财。£_L平面OECB,连接MB,MC得到图2,点N为MC的中点.

（1）当EN〃平面M6O时，求；I的值；

（2）试探究：随着义值的变化，二面角8-石的大小是否改变？如果改变，请求出实

数4与二面角平面角的正弦值的函数关系：如果不改变，请求出二面角8-MD-E的正弦值

大小.

【答案】（1）j（2）苧

【详解】

（1）取M8的中点为P,连接DP,PN,

因为MN=CMMP=BP,所以A/PII8C,又DEII8C,所以NPIIDE即A/,E,D,P四点共

面，又ENU面BMD,E/Vc®NEDP,平面A/EOPc平面M8O=DP,所以E/VIIPD,即NEDP为

平行四边形，所以A/PIIDE,且NP=DE,即。七即2号

(2)解：取DE的中点。，由平面MD£_L平面DEC8,且MO_LOE,所以MO_L平面DEC8,

如图建立空间直角坐标系，不妨设8c=2,则皿0,0,向)，0(入，0,0),B(l,x^(l-2),0)

所以而=(40,_&),而=0_九6(1_/1),0)

一MDm=^x->/32z=0

设平面BMD的法向量为m=(x,y,z)则｛__/\r/\

、)[BDw=(l-2)x+V3(l-A)j=0

令即而=(G,T1)又平面EMD的法向量7=(0,1,0)

所以COS(正,0=忑=~即随着入值的变化，二面角8-MO-E的