中考数学总复习《特殊平行四边形》专项测试题(附答案)

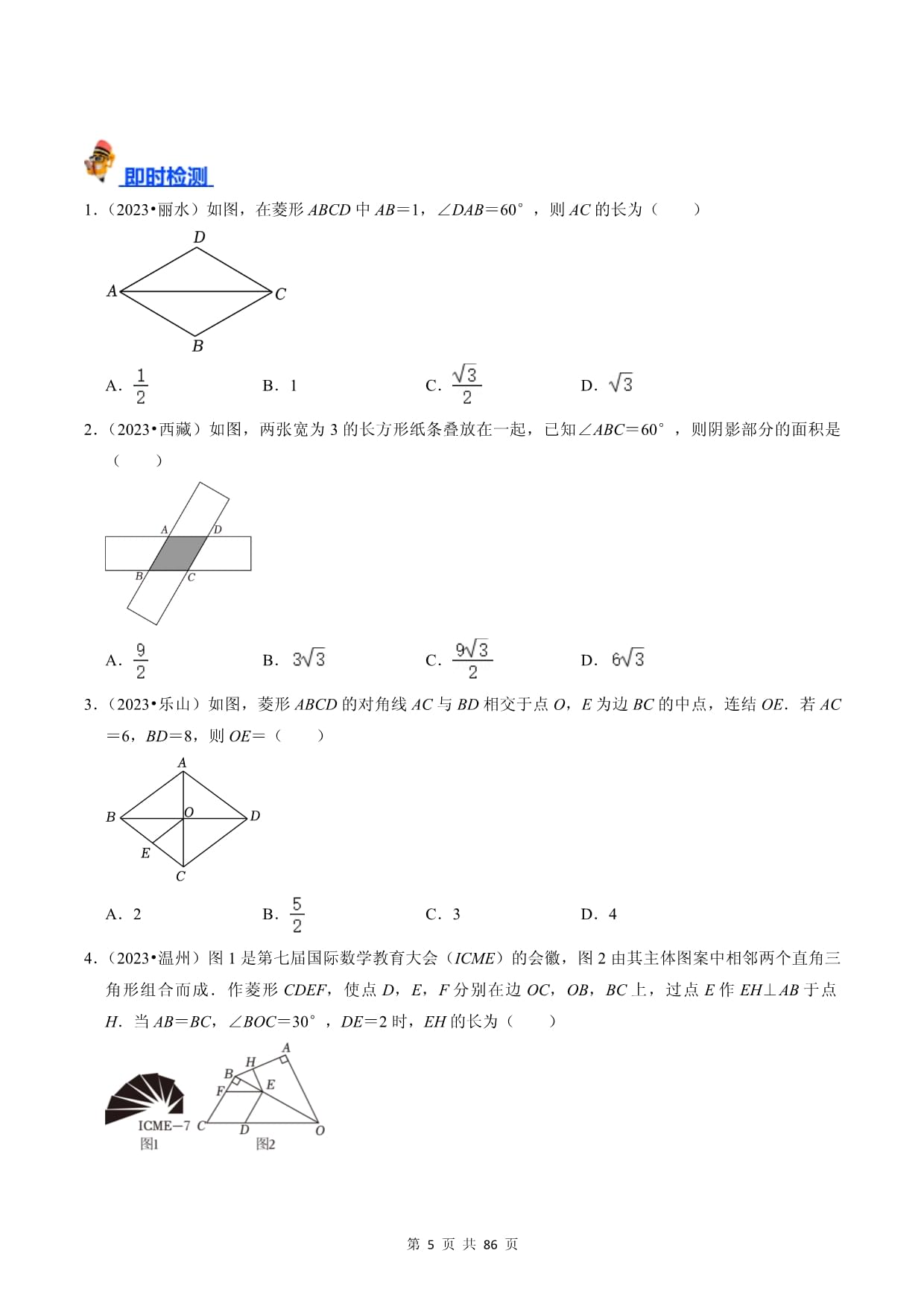
第页中考数学总复习《特殊平行四边形》专项测试题(附答案)（考试时间：90分钟，试卷满分：100分）学校:___________班级：___________姓名：___________考号：___________1.掌握矩形、菱形、正方形的概念和性质；2.了解平行四边形、矩形、菱形、正方形形之间的关系；3.探索并掌握四边形是矩形、菱形、正方形的条条件考点1：矩形的性质和判定（1）性质：矩形是特殊的平行四边形，它具有平行四边形的所有性质，还具有自己独特的性质：①边的性质：对边平行且相等．②角的性质：四个角都是直角．③对角线性质：对角线互相平分且相等．④对称性：矩形是中心对称图形，也是轴对称图形．直角三角形斜边上的中线等于斜边的一半．直角三角形中角所对的边等于斜边的一半．点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得．考点2：矩形的判定判定①：有一个角是直角的平行四边形是矩形．判定②：对角线相等的平行四边形是矩形．判定③：有三个角是直角的四边形是矩形．考点3：菱形的性质（1）菱形的四条边都相等；（2）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。考点4：菱形的判定定理（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四条边相等的四边形是菱形。考点5：菱形的面积S=ah=mn/2（菱形底边长为a，高为h，两条对角线长分别为m和n）考点6：正方形的性质：1、正方形具有平行四边形和菱形的所有性质。2、正方形的四个角都是直角，四条边都相等。3、正方形对边平行且相等。4、正方形的对角线互相垂直平分且相等，对角线平分对角；5、正方形的两条对角线把正方形分成四个全等的等腰直角三角形；6、正方形既是中心对称图形，也是轴对称图形.考点7：正方形的判定：1）有一个角是直角的菱形是正方形；2）对角线相等的菱形是正方形；3）一组邻边相等的矩形是正方形；4）对角线互相垂直的矩形是正方形；5）对角线互相垂直平分且相等的四边形是正方形；6）四条边都相等，四个角都是直角的四边形是正方形.正方形的面积公式：面积=边长×边长=12【题型1：矩形的性质和判定】【典例1】（2023•大庆）如图，在平行四边形ABCD中E为线段CD的中点，连接AC，AE，延长AE，BC交于点F，连接DF，∠ACF＝90°．（1）求证：四边形ACFD是矩形；（2）若CD＝13，CF＝5，求四边形ABCE的面积．1．（2023•呼和浩特）如图，矩形ABCD中对角线BD的垂直平分线MN分别交AD，BC于点M，N．若AM＝1，BN＝2，则BD的长为（）A． B．3 C． D．2．（2023•杭州）如图，矩形ABCD的对角线AC，BD相交于点O．若∠AOB＝60°，则＝（）A． B． C． D．3．（2023•南通）如图，四边形ABCD是矩形，分别以点B，D为圆心，线段BC，DC长为半径画弧，两弧相交于点E，连接BE，DE，BD．若AB＝4，BC＝8，则∠ABE的正切值为（）A． B． C． D．4．（2023•新疆）如图，AD和BC相交于点O，∠ABO＝∠DCO＝90°，OB＝OC，点E、F分别是AO、DO的中点．（1）求证：OE＝OF；（2）当∠A＝30°时，求证：四边形BECF是矩形．5．（2022•泰州）如图，线段DE与AF分别为△ABC的中位线与中线．（1）求证：AF与DE互相平分；（2）当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由．【题型2：菱形的性质和判定】【典例2】（2022•广元）如图，在四边形ABCD中AB∥CD，AC平分∠DAB，AB＝2CD，E为AB中点，连结CE．（1）求证：四边形AECD为菱形；（2）若∠D＝120°，DC＝2，求△ABC的面积．1．（2023•丽水）如图，在菱形ABCD中AB＝1，∠DAB＝60°，则AC的长为（）A． B．1 C． D．2．（2023•西藏）如图，两张宽为3的长方形纸条叠放在一起，已知∠ABC＝60°，则阴影部分的面积是（）A． B． C． D．3．（2023•乐山）如图，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连结OE．若AC＝6，BD＝8，则OE＝（）A．2 B． C．3 D．44．（2023•温州）图1是第七届国际数学教育大会（ICME）的会徽，图2由其主体图案中相邻两个直角三角形组合而成．作菱形CDEF，使点D，E，F分别在边OC，OB，BC上，过点E作EH⊥AB于点H．当AB＝BC，∠BOC＝30°，DE＝2时，EH的长为（）A． B． C． D．5．（2023•湘西州）如图，四边形ABCD是平行四边形，BM∥DN，且分别交对角线AC于点M，N，连接MD，BN．（1）求证：∠DMN＝∠BNM；（2）若∠BAC＝∠DAC．求证：四边形BMDN是菱形．6．（2022•聊城）如图，△ABC中点D是AB上一点，点E是AC的中点，过点C作CF∥AB，交DE的延长线于点F．（1）求证：AD＝CF；（2）连接AF，CD．如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF是菱形，证明你的结论．【题型2：正方形的性质和判定】【典例2】（2022•邵阳）如图，在菱形ABCD中对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．求证：四边形AECF是正方形．1．（2023•常德）如图1，在正方形ABCD中对角线AC、BD相交于点O，E，F分别为AO，DO上的一点，且EF∥AD，连接AF，DE．若∠FAC＝15°，则∠AED的度数为（）A．80° B．90° C．105° D．115°2．（2021•玉林）一个四边形顺次添加下列条件中的三个条件便得到正方形：a．两组对边分别相等b．一组对边平行且相等c．一组邻边相等d．一个角是直角顺次添加的条件：①a→c→d②b→d→c③a→b→c则正确的是（）A．仅① B．仅③ C．①② D．②③3．（2023•丹东）如图，在正方形ABCD中AB＝12，点E，F分别在边BC，CD上，AE与BF相交于点G，若BE＝CF＝5，则BG的长为．一．选择题（共9小题）1．矩形的两条对角线的夹角为60度，对角线长为15，则矩形的较短边长为（）A．12 B．10 C．7.5 D．52．如图，在菱形ABCD中点E，F分别是AC，AB的中点，如果EF＝3，那么菱形ABCD的周长为（）A．24 B．18 C．12 D．93．用边长为1的正方形做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积为原正方形面积的（）A． B． C． D．不能确定4．下列说法中不正确的是（）A．有一个角是直角的平行四边形是正方形 B．对角线相等的平行四边形是矩形 C．对角线互相平分且垂直的四边形是菱形 D．对边分别相等的四边形是平行四边形5．如图，矩形ABCD的对角线AC，BD交于点O，AB＝3，BC＝4，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为（）A． B． C． D．6．菱形具有而矩形不具有的性质是（）A．对边相等 B．对角相等 C．对角线互相平分 D．对角线互相垂直7．如图，在菱形ABCD中AB＝5，对角线AC＝6．若过点A作AE⊥BC，垂足为E，则AE的长为（）A．4 B．2.4 C．4.8 D．58．如图所示，在正方形ABCD中O是对角线AC、BD的交点，过O作OE⊥OF，分别交AB、BC于E、F，若AE＝4，CF＝3，则EF的长为（）A．3 B．4 C．5 D．69．如图，点E、F分别在矩形ABCD的边AB、BC上，且∠EFD＝90°，若BF＝3，BE＝4，CD＝9，则FC的长为（）A．12 B．13 C．14 D．15二．填空题（共4小题）10．如图，矩形ABCD的对角线AC，BD相交于点O，过点O作OE⊥BD，交BC于点E，若，CE＝1，则BE的长为．11．如图，在边长为2的正方形ABCD中E，F分别是边DC，CB上的动点，且始终满足DE＝CF，AE，DF交于点P，则∠APD的度数为；连接CP，线段CP的最小值为．12．如图，直线l过正方形ABCD的顶点B，点A、点C到直线l的距离分别为1和2，则正方形的边长是．13．已知：如图，在长方形ABCD中AB＝4，AD＝6，延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，当点P运动秒时，△ABP和△DCE全等．三．解答题（共3小题）14．如图，在四边形ABCD中∠BAC＝90°，E是BC的中点，AD∥BC，AE∥DC，EF⊥CD于点F．（1）求证：四边形AECD是菱形；（2）若AB＝6，AC＝8，求EF的长．15．如图所示，O是矩形ABCD的对角线的交点，DE∥AC，CE∥BD．（1）求证：OE⊥DC．（2）若∠AOD＝120°，DE＝2，求矩形ABCD的面积．16．将两张长为8，宽为4的矩形纸片如图叠放．（1）判断四边形AGCH的形状，并说明理由；（2）求四边形AGCH的面积．一．选择题（共7小题）1．如图，在正方形ABCD中E、F分别是AB，BC的中点，CE，DF交于点G，连接AG，下列结论：①CE＝DF；②CE⊥DF；③∠AGE＝∠CDF；④∠EAG＝30°，其中正确的结论是（）A．①② B．①③ C．①②④ D．①②③2．已知：如图，正方形ABCD中AB＝4，AC，BD相交于点O，E，F分别为边BC，CD上的动点（点E，F不与线段BC，CD的端点重合）且BE＝CF，连接OE，OF，EF．在点E，F运动的过程中有下列四个结论：①△OEF始终是等腰直角三角形；②△OEF面积的最小值是2；③至少存在一个△ECF，使得△ECF的周长是4+2；④四边形OECF的面积始终是4．所有正确结论的序号是（）A．①②③ B．③④ C．①②④ D．①②③④3．如图，正方形ABCD和长方形AEFG的面积相等，且四边形BEFH也是正方形，欧几里得在《几何原本》中利用该图得到了：BH2＝CH×GH．设AB＝a，CH＝b．若ab＝5，则图中阴影部分的周长是（）A．6 B．8 C．10 D．204．如图，在正方形ABCD中AB＝4，E，F分别为边AB，BC的中点，连接AF，DE，点G，H分别为DE，AF的中点，连接GH，则GH的长为（）A． B．1 C． D．25．如图，正方形ABCD和正方形CEFG中点D在CG上，已知BC＝1，CE＝7，点H是AF的中点，则CH的长是（）A．5 B．3.5 C．4 D．6．如图，在矩形ABCD中AB＝2，AD＝1，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2 B．4 C． D．27．如图，▱ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC＝60°，AB＝BC，连接OE，下列结论：①∠CAD＝30°；②OD＝AB；③S▱ABCD＝AC•CD；④S四边形OECD＝S△AOD，其中成立的个数为（）A．1个 B．2个 C．3个 D．4个二．填空题（共5小题）8．如图，在正方形ABCD中AB＝3cm，延长BC到点E，使CE＝1cm，连接DE，动点P从点A出发，以每秒1cm的速度沿AB→BC→CD→DA向终点A运动．设点P的运动时间为t秒，当△PBC和△DCE全等时，t的值为．9．如图，在菱形ABCD中∠B＝45°，E、F分别是边CD，BC上的动点，连接AE、EF，G、H分别为AE、EF的中点，连接GH．若GH的最小值为3，则BC的长为．10．如图，在菱形ABCD中对角线AC，BD交于点O，点E为AB的中点，点F在OD上，DF＝OF，连接EF交OA于点G，若OG＝1，连接CE，S△BEC＝12，则线段CE的长为．11．如图，在平面直角坐标系中矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC边上运动，点Q是坐标平面内的任意一点．若以O，D，P，Q为顶点的四边形是边长为5的菱形时，则点Q的坐标为．12．如图，在△ABC中∠C＝90°，AC＝6，BC＝8，点D在AB边上，DE⊥AC，DF⊥BC，垂足分别为点E、F，连接EF，则线段EF的最小值等于．三．解答题（共5小题）13．【问题情境】：如图1，点E为正方形ABCD内一点，AE＝2，BE＝4，∠AEB＝90°，将直角三角形ABE绕点A逆时针方向旋转α度（0≤α≤180°）点B、E的对应点分别为点B′、E′．【问题解决】：（1）如图2，在旋转的过程中点B′落在了AC上，求此时CB′的长；（2）若α＝90°，如图3，得到△ADE′（此时B′与D重合），延长BE交DE′于点F①试判断四边形AEFE′的形状，并说明理由；②连接CE，求CE的长；（3）在直角三角形ABE绕点A逆时针方向旋转过程中直接写出线段CE′长度的取值范围．14．已知：如图（1），在平面直角坐标系中点A、点B分别在x轴、y轴的正半轴上，点C在第一象限，∠ACB＝90°，AC＝BC，点A坐标为（m，0），点C横坐标为n，且m2+n2﹣2m﹣8n+17＝0．（1）分别求出点A、点B、点C的坐标；（2）如图（2），点D为边AB中点，以点D为顶点的直角∠EDF两边分别交边BC于E，交边AC于F，①求证：DE＝DF；②求证：S四边形DECF＝S△ABC；（3）在坐标平面内有点G（点G不与点A重合），使得△BCG是以BC为直角边的等腰直角三角形，请直接写出满足条件的点G的坐标．15．综合与实践：【思考尝试】（1）数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中E是边AB上一点，DF⊥CE于点F，GD⊥DF，AG⊥DG，AG＝CF，试猜想四边形ABCD的形状，并说明理由；【实践探究】（2）小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD中E是边AB上一点，DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G，可以用等式表示线段FH，AH，CF的数量关系，请你思考并解答这个问题；【拓展迁移】（3）小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中E是边AB上一点，AH⊥CE于点H，点M在CH上，且AH＝HM，连接AM，BH，可以用等式表示线段CM，BH的数量关系，请你思考并解答这个问题．16．回答问题（1）【初步探索】如图1，在四边形ABCD中AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系，小王同学探究此问题的方法是：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论是；（2）【灵活运用】如图2，若在四边形ABCD中AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】已知在四边形ABCD中∠ABC+∠ADC＝180°，AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3，仍然满足EF＝BE+FD，请直接写出∠EAF与∠DAB的数量关系．17．（1）如图1，在正方形ABCD中点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则的值为；（2）如图2，在矩形ABCD中AD＝5，CD＝3，点E是AD上的一点，连接CE，BD，且CE⊥BD，则的值为；（3）如图3，在四边形ABCD中∠A＝∠B＝90°，点E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：；（4）如图4，在Rt△ABD中∠BAD＝90°，AB＝3，AD＝9，将△ABD沿BD翻折，点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．请问．是定值吗？若是，直接写出这个定值，若不是，请说明理由．1．（2023•湘潭）如图，菱形ABCD中连接AC，BD，若∠1＝20°，则∠2的度数为（）A．20° B．60° C．70° D．80°2．（2023•内蒙古）如图，在菱形ABCD中AB＝4，∠A＝120°，顺次连接菱形ABCD各边中点E、F、G、H，则四边形EFGH的周长为（）A．4+2 B．6+2 C．4+4 D．6+43．（2023•西藏）如图，矩形ABCD中AC和BD相交于点O，AD＝3，AB＝4，点E是CD边上一点，过点E作EH⊥BD于点H，EG⊥AC于点G，则EH+EG的值是（）A．2.4 B．2.5 C．3 D．44．（2023•青岛）如图，在正方形ABCD中点E，F分别是AB，CD的中点，AF，DE相交于点M，G为BC上一点，N为EG的中点．若BG＝3，CG＝1，则线段MN的长度为（）A． B． C．2 D．5．（2023•台湾）如图，矩形ABCD中AB＝6，AD＝8，且有一点P从B点沿着BD往D点移动，若过P点作AB的垂线交AB于E点，过P点作AD的垂线交AD于F点，则EF的长度最小为多少（）A． B． C．5 D．76．（2023•绵阳）如图，在边长为4的正方形ABCD中点G是BC上的一点，且BG＝3GC，DE⊥AG于点E，BF∥DE，且交AG于点F，则tan∠EDF的值为（）A． B． C． D．7．（2023•宜宾）如图，边长为6的正方形ABCD中M为对角线BD上的一点，连接AM并延长交CD于点P，若PM＝PC，则AM的长为（）A．3（﹣1） B．3（3﹣2） C．6（﹣1） D．6（3﹣2）8．（2023•黑龙江）如图，在矩形ABCD中对角线AC，BD相交于点O，试添加一个条件，使得矩形ABCD为正方形．9．（2023•宁夏）如图，在边长为2的正方形ABCD中点E在AD上，连接EB，EC．则图中阴影部分的面积是．10．（2023•广西）如图，在边长为2的正方形ABCD中E，F分别是BC，CD上的动点，M，N分别是EF，AF的中点，则MN的最大值为．11．（2023•扬州）如图，已知正方形ABCD的边长为1，点E、F分别在边AD、BC上，将正方形沿着EF翻折，点B恰好落在CD边上的点B′处，如果四边形ABFE与四边形EFCD的面积比为3：5，那么线段FC的长为．12．（2023•岳阳）如图，点M在▱ABCD的边AD上，BM＝CM，请从以下三个选项中①∠1＝∠2；②AM＝DM；③∠3＝∠4，选择一个合适的选项作为已知条件，使▱ABCD为矩形．（1）你添加的条件是（填序号）；（2）添加条件后，请证明▱ABCD为矩形．13．（2023•张家界）如图，已知点A，D，C，B在同一条直线上，且AD＝BC，AE＝BF，CE＝DF．（1）求证：AE∥BF；（2）若DF＝FC时，求证：四边形DECF是菱形．14．（2023•十堰）如图，▱ABCD的对角线AC，BD交于点O，分别以点B，C为圆心，AC，BD长为半径画弧，两弧交于点P，连接BP，CP．（1）试判断四边形BPCO的形状，并说明理由；（2）请说明当▱ABCD的对角线满足什么条件时，四边形BPCO是正方形？15．（2023•云南）如图，平行四边形ABCD中AE、CF分别是∠BAD、∠BCD的平分线，且E、F分别在边BC、AD上，AE＝AF．（1）求证：四边形AECF是菱形；（2）若∠ABC＝60°，△ABE的面积等于，求平行线AB与DC间的距离．参考答案与解析1.掌握矩形、菱形、正方形的概念和性质；2.了解平行四边形、矩形、菱形、正方形形之间的关系；3.探索并掌握四边形是矩形、菱形、正方形的条条件考点1：矩形的性质和判定（1）性质：矩形是特殊的平行四边形，它具有平行四边形的所有性质，还具有自己独特的性质：①边的性质：对边平行且相等．②角的性质：四个角都是直角．③对角线性质：对角线互相平分且相等．④对称性：矩形是中心对称图形，也是轴对称图形．直角三角形斜边上的中线等于斜边的一半．直角三角形中角所对的边等于斜边的一半．点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得．考点2：矩形的判定判定①：有一个角是直角的平行四边形是矩形．判定②：对角线相等的平行四边形是矩形．判定③：有三个角是直角的四边形是矩形．考点3：菱形的性质（1）菱形的四条边都相等；（2）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。考点4：菱形的判定定理（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四条边相等的四边形是菱形。考点5：菱形的面积S=ah=mn/2（菱形底边长为a，高为h，两条对角线长分别为m和n）考点6：正方形的性质：1、正方形具有平行四边形和菱形的所有性质。2、正方形的四个角都是直角，四条边都相等。3、正方形对边平行且相等。4、正方形的对角线互相垂直平分且相等，对角线平分对角；5、正方形的两条对角线把正方形分成四个全等的等腰直角三角形；6、正方形既是中心对称图形，也是轴对称图形.考点7：正方形的判定：1）有一个角是直角的菱形是正方形；2）对角线相等的菱形是正方形；3）一组邻边相等的矩形是正方形；4）对角线互相垂直的矩形是正方形；5）对角线互相垂直平分且相等的四边形是正方形；6）四条边都相等，四个角都是直角的四边形是正方形.正方形的面积公式：面积=边长×边长=12【题型1：矩形的性质和判定】【典例1】（2023•大庆）如图，在平行四边形ABCD中E为线段CD的中点，连接AC，AE，延长AE，BC交于点F，连接DF，∠ACF＝90°．（1）求证：四边形ACFD是矩形；（2）若CD＝13，CF＝5，求四边形ABCE的面积．【答案】（1）证明过程见解答；（2）45．【解答】（1）证明：∵四边形ABCD是平行四边形∴AD∥BC∴∠ADE＝∠FCE，∠DAE＝∠CFE∵E为线段CD的中点∴DE＝CE∴△ADE≌△FCE（AAS）∴AE＝FE∴四边形ACFD是平行四边形∵∠ACF＝90°∴四边形ACFD是矩形；（2）解：∵四边形ACFD是矩形∴∠CFD＝90°，AC＝DF∵CD＝13，CF＝5∴DF＝＝＝12∵△ADE≌△FCE∵△CEF的面积＝△ACF的面积＝5×12＝15平行四边形ABCD的面积＝BC•AC＝5×12＝60∴四边形ABCE的面积＝平行四边形ABCD的面积﹣△CEF的面积＝60﹣15＝45．1．（2023•呼和浩特）如图，矩形ABCD中对角线BD的垂直平分线MN分别交AD，BC于点M，N．若AM＝1，BN＝2，则BD的长为（）A． B．3 C． D．【答案】A【解答】解：由题意，连接BM，记BD与MN交于点O．∵线段MN垂直平分BD∴BO＝DO，BM＝DM．∵四边形ABCD是矩形∴AD∥BC．∴∠MDO＝∠NBO．又∠DOM＝∠BON∴△DMO≌△BNO（ASA）．∴DM＝BN＝BM＝2．在Rt△BAM中∴AB＝＝．∴在Rt△BAD中可得，BD＝＝2．故选：A．2．（2023•杭州）如图，矩形ABCD的对角线AC，BD相交于点O．若∠AOB＝60°，则＝（）A． B． C． D．【答案】D【解答】解：∵四边形ABCD是矩形∴AO＝BO＝CO＝DO∵∠AOB＝60°∴△ABO是等边三角形∴∠BAO＝60°∴∠ACB＝30°∴BC＝AB∴＝故选：D．3．（2023•南通）如图，四边形ABCD是矩形，分别以点B，D为圆心，线段BC，DC长为半径画弧，两弧相交于点E，连接BE，DE，BD．若AB＝4，BC＝8，则∠ABE的正切值为（）A． B． C． D．【答案】C【解答】解：∵BE＝BC，DE＝CD，BD＝BD∴△CBD≌△EBD（SSS）∴∠CBD＝∠EBD∵四边形ABCD是矩形∴AD∥BC，AD＝BC＝8，∠A＝90°∴∠ADB＝∠CBD∴∠ADB＝∠EBD∴OB＝OD设AO＝x，则OD＝8﹣x∴OB＝8﹣x由勾股定理得：AB2+AO2＝OB2∴42+x2＝（8﹣x）2∴x＝3∴tan∠ABE＝＝．故选：C．4．（2023•新疆）如图，AD和BC相交于点O，∠ABO＝∠DCO＝90°，OB＝OC，点E、F分别是AO、DO的中点．（1）求证：OE＝OF；（2）当∠A＝30°时，求证：四边形BECF是矩形．【答案】（1）见解析；（2）见解析．【解答】证明：（1）∵∠ABO＝∠DCO＝90°∴AB∥CD∴∠A＝∠D在△AOB与△DOC中∴△AOB≌△DOC（AAS）∴AO＝DO∵点E、F分别是AO、DO的中点∴∴OE＝OF；（2）∵OB＝OC，OE＝OF∴四边形BECF是平行四边形∵∠A＝30°∴∵OE＝OF∴∴∠EBF＝90°∴四边形BECF是矩形．5．（2022•泰州）如图，线段DE与AF分别为△ABC的中位线与中线．（1）求证：AF与DE互相平分；（2）当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由．【答案】见试题解答内容【解答】（1）证明：∵点D是AB的中点∴AD＝AB∵点E是AC的中点，点F是BC的中点∴EF是△ABC的中位线∴EF∥AB，EF＝AB∴EF＝AD∴四边形ADFE是平行四边形∴AF与DE互相平分；（2）解：当AF＝BC时，四边形ADFE为矩形理由：∵线段DE为△ABC的中位线∴DE＝BC∵AF＝BC∴AF＝DE由（1）得：四边形ADFE是平行四边形∴四边形ADFE为矩形．【题型2：菱形的性质和判定】【典例2】（2022•广元）如图，在四边形ABCD中AB∥CD，AC平分∠DAB，AB＝2CD，E为AB中点，连结CE．（1）求证：四边形AECD为菱形；（2）若∠D＝120°，DC＝2，求△ABC的面积．【答案】（1）见解析过程；（2）2．【解答】（1）证明：∵E为AB中点∴AB＝2AE＝2BE∵AB＝2CD∴CD＝AE又∵AE∥CD∴四边形AECD是平行四边形∵AC平分∠DAB∴∠DAC＝∠EAC∵AB∥CD∴∠DCA＝∠CAB∴∠DCA＝∠DAC∴AD＝CD∴平行四边形AECD是菱形；（2）∵四边形AECD是菱形，∠D＝120°∴AD＝CD＝CE＝AE＝2，∠D＝120°＝∠AEC∴AE＝CE＝BE，∠CEB＝60°∴∠CAE＝30°＝∠ACE，△CEB是等边三角形∴BE＝BC＝EC＝2，∠B＝60°∴∠ACB＝90°∴AC＝BC＝2∴S△ABC＝×AC×BC＝×2×2＝2．1．（2023•丽水）如图，在菱形ABCD中AB＝1，∠DAB＝60°，则AC的长为（）A． B．1 C． D．【答案】D【解答】解：如图，连接BD交AC于点O∵四边形ABCD是菱形，∠DAB＝60°∴OA＝OC，∠BAO＝∠DAB＝30°，AC⊥BD∴∠AOB＝90°∴OB＝AB＝∴OA＝＝＝∴AC＝2OA＝故选：D．2．（2023•西藏）如图，两张宽为3的长方形纸条叠放在一起，已知∠ABC＝60°，则阴影部分的面积是（）A． B． C． D．【答案】D【解答】解：过点A作AE⊥BC于E，AF⊥CD于F∵两条纸条宽度相同∴AE＝AF．∵AB∥CD，AD∥BC∴四边形ABCD是平行四边形．∵S▱ABCD＝BC•AE＝CD•AF．又∵AE＝AF．∴BC＝CD∴四边形ABCD是菱形，在Rt△AEB中∠AEB＝90°，∠ABC＝60°，AE＝3cm∴AB＝（cm）∴BC＝2cm∴四边形ABCD的面积＝AE•BC＝6cm2．故选：D．3．（2023•乐山）如图，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连结OE．若AC＝6，BD＝8，则OE＝（）A．2 B． C．3 D．4【答案】B【解答】解：∵四边形ABCD是菱形∴OC＝AC，OB＝BD，AC⊥BD∵AC＝6，BD＝8∴OC＝3，OB＝4∴CB＝＝5∵E为边BC的中点∴OE＝BC＝．故选：B．4．（2023•温州）图1是第七届国际数学教育大会（ICME）的会徽，图2由其主体图案中相邻两个直角三角形组合而成．作菱形CDEF，使点D，E，F分别在边OC，OB，BC上，过点E作EH⊥AB于点H．当AB＝BC，∠BOC＝30°，DE＝2时，EH的长为（）A． B． C． D．【答案】C【解答】解：∵四边形CDEF是菱形，DE＝2∴CD＝DE＝CF＝EF＝2，CF∥DE，CD∥EF∵∠CBO＝90°，∠BOC＝30°∴OD＝2DE＝4，OE＝DE＝2∴CO＝CD+DO＝6∴BC＝AB＝CD＝3，OB＝BC＝3∵∠A＝90°∴＝＝3∵EF∥CD∴∠BEF＝∠BOC＝30°∴∵EH⊥AB∴EH∥OA∴△BHE∽△BAO∴∴∴EH＝故选：C．5．（2023•湘西州）如图，四边形ABCD是平行四边形，BM∥DN，且分别交对角线AC于点M，N，连接MD，BN．（1）求证：∠DMN＝∠BNM；（2）若∠BAC＝∠DAC．求证：四边形BMDN是菱形．【答案】（1）见解析；（2）见解析．【解答】证明：（1）连接BD，交AC于点O，如图：∵四边形ABCD是平行四边形∴OB＝OD∵BM∥DN∴∠MBO＝∠NDO又∠BOM＝∠DON∴△BOM≌△DON（ASA）∴BM＝DN∴四边形BMDN为平行四边形∴BN∥DM∴∠DMN＝∠BNM；（2）∵四边形ABCD是平行四边形∴BC∥AD∴∠BCA＝∠DAC∵∠BAC＝∠DAC∴∠BAC＝∠BCA∴AB＝BC∴四边形ABCD是菱形∴AC⊥BD∴MN⊥BD∴平行四边形BMDN是菱形．6．（2022•聊城）如图，△ABC中点D是AB上一点，点E是AC的中点，过点C作CF∥AB，交DE的延长线于点F．（1）求证：AD＝CF；（2）连接AF，CD．如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF是菱形，证明你的结论．【答案】（1）证明见解答过程；（2）当AC⊥BC时，四边形ADCF是菱形，证明见解答过程．【解答】（1）证明：∵CF∥AB∴∠ADF＝∠CFD，∠DAC＝∠FCA∵点E是AC的中点∴AE＝CE∴△ADE≌△CFE（AAS）∴AD＝CF；（2）解：当AC⊥BC时，四边形ADCF是菱形，证明如下：由（1）知，AD＝CF∵AD∥CF∴四边形ADCF是平行四边形∵AC⊥BC∴△ABC是直角三角形∵点D是AB的中点∴CD＝AB＝AD∴四边形ADCF是菱形．【题型2：正方形的性质和判定】【典例2】（2022•邵阳）如图，在菱形ABCD中对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．求证：四边形AECF是正方形．【答案】证明过程见解答部分．【解答】证明：∵四边形ABCD是菱形∴AC⊥BD，OA＝OC，OB＝OD∵BE＝DF∴OE＝OF∴四边形AECF是菱形；∵OE＝OA＝OF∴OE＝OF＝OA＝OC，即EF＝AC∴平行四边形AECF是矩形，即∠AEC＝90°∴菱形AECF是正方形．1．（2023•常德）如图1，在正方形ABCD中对角线AC、BD相交于点O，E，F分别为AO，DO上的一点，且EF∥AD，连接AF，DE．若∠FAC＝15°，则∠AED的度数为（）A．80° B．90° C．105° D．115°【答案】C【解答】解：∵四边形ABCD为正方形∴OA＝OD，∠OBC＝∠OCB＝∠OAD＝∠ODA＝45°∵EF∥BC∴∠OEF＝∠OCB＝45°，∠OFE＝∠OBC＝45°∴∠OEF＝∠OFE＝45°∴∠AEF＝∠DFE＝135°，OE＝OF∵OA＝OD∴AE＝DF在△AEF和△DFE中AE＝DF，∠AEF＝∠DFE＝135°，EF＝FE∴△AEF≌△DFE（SAS）∴∠CAF＝∠FDE＝15°∴∠ADE＝∠ODA﹣∠FDE＝45°﹣15°＝30°∴∠AED＝180°﹣∠OAD﹣∠ADE＝180°﹣45°﹣30°＝105°．故选：C．2．（2021•玉林）一个四边形顺次添加下列条件中的三个条件便得到正方形：a．两组对边分别相等b．一组对边平行且相等c．一组邻边相等d．一个角是直角顺次添加的条件：①a→c→d②b→d→c③a→b→c则正确的是（）A．仅① B．仅③ C．①② D．②③【答案】C【解答】解：①由a得到两组对边分别相等的四边形是平行四边形，添加c即一组邻边相等的平行四边形是菱形，再添加d即一个角是直角的菱形是正方形，故①正确；②由b得到一组对边平行且相等的四边形是平行四边形，添加d即有一个角是直角的平行四边形是矩形，再添加c即一组邻边相等的矩形是正方形，故②正确；③由a得到两组对边分别相等的四边形是平行四边形，添加b得到一组对边平行且相等的平行四边形仍是平行四边形，再添加c即一组邻边相等的平行四边形是菱形，不能得到四边形是正方形，故③不正确；故选：C．3．（2023•丹东）如图，在正方形ABCD中AB＝12，点E，F分别在边BC，CD上，AE与BF相交于点G，若BE＝CF＝5，则BG的长为．【答案】．【解答】解：∵四边形ABCD是正方形∴∠ABE＝∠C＝90°，AB＝BC∵BE＝CF∴△ABE≌△BCF（SAS）∴∠BAE＝∠CBF∵∠CBF+∠ABG＝90°∴∠BAE+∠ABG＝90°∴∠BGE＝90°∴∠BGE＝∠C又∵∠EBG＝∠FBC∴△EBG∽△FBC∴∵BC＝AB＝12，CF＝BE＝5∴BF＝∴∴．故答案为：．一．选择题（共9小题）1．矩形的两条对角线的夹角为60度，对角线长为15，则矩形的较短边长为（）A．12 B．10 C．7.5 D．5【答案】C【解答】解：如图所示：矩形ABCD，对角线AC＝BD＝15，∠AOD＝∠BOC＝60°∵四边形ABCD是矩形∴OA＝OD＝OC＝OB＝×15＝7.5（矩形的对角线互相平分且相等）又∵∠AOD＝∠BOC＝60°∴OA＝OD＝AD＝7.5∵∠COD＝120°＞∠AOD＝60°∴AD＜DC所以该矩形较短的一边长为7.5故选：C．2．如图，在菱形ABCD中点E，F分别是AC，AB的中点，如果EF＝3，那么菱形ABCD的周长为（）A．24 B．18 C．12 D．9【答案】A【解答】解：∵E、F分别是AC、AB的中点∴EF是△ABC的中位线∴BC＝2EF＝2×3＝6∴菱形ABCD的周长＝4×6＝24．故选：A．3．用边长为1的正方形做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积为原正方形面积的（）A． B． C． D．不能确定【答案】A【解答】解：读图可得，阴影部分的面积为原正方形的面积的一半，则阴影部分的面积为1×1÷2＝；是原正方形的面积的一半；故选：A．4．下列说法中不正确的是（）A．有一个角是直角的平行四边形是正方形 B．对角线相等的平行四边形是矩形 C．对角线互相平分且垂直的四边形是菱形 D．对边分别相等的四边形是平行四边形【答案】A【解答】解：A、一个角是直角的平行四边形是矩形，故原说法错误，此选项符合题意；B、对角线相等的平行四边形是矩形，故原说法正确，此选项不合题意；C、对角线互相平分且垂直的四边形是菱形，故原说法正确，此选项不合题意；D、两组对边分别平行的四边形是平行四边形；故原说法正确，此选项不合题意；故选：A．5．如图，矩形ABCD的对角线AC，BD交于点O，AB＝3，BC＝4，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为（）A． B． C． D．【答案】C【解答】解：∵AB＝3，BC＝4∴矩形ABCD的面积为12，AC＝∴AO＝DO＝AC＝∵对角线AC，BD交于点O∴△AOD的面积为3∵EO⊥AO，EF⊥DO∴S△AOD＝S△AOE+S△DOE，即3＝AO×EO+DO×EF∴3＝××EO+×EF∴5（EO+EF）＝12∴EO+EF＝故选：C．6．菱形具有而矩形不具有的性质是（）A．对边相等 B．对角相等 C．对角线互相平分 D．对角线互相垂直【答案】D【解答】解：A、对边相等，是菱形和矩形都具有的性质，故选项A不符合题意；B、对角相等，是矩形和菱形都具有的性质，故选项B不符合题意；C、对角线互相平分，是矩形和菱形都具有的性质，故选项C不符合题意；D、对角线互相垂直，是菱形具有而矩形不具有的性质，故选项D符合题意；故选：D．7．如图，在菱形ABCD中AB＝5，对角线AC＝6．若过点A作AE⊥BC，垂足为E，则AE的长为（）A．4 B．2.4 C．4.8 D．5【答案】C【解答】解：连接BD，交AC于O点∵四边形ABCD是菱形∴AB＝BC＝CD＝AD＝5∴AC⊥BD，AO＝AC，BD＝2BO∴∠AOB＝90°∵AC＝6∴AO＝3∴BO＝＝4∴DB＝8∴菱形ABCD的面积是×AC•DB＝×6×8＝24∴BC•AE＝24∵BC＝AB＝5∴AE＝故选：C．8．如图所示，在正方形ABCD中O是对角线AC、BD的交点，过O作OE⊥OF，分别交AB、BC于E、F，若AE＝4，CF＝3，则EF的长为（）A．3 B．4 C．5 D．6【答案】C【解答】解：∵四边形ABCD是正方形∴OB＝OC，∠OBE＝∠OCF＝45°，AC⊥BD又∵OE⊥OF∴∠EOB+∠BOF＝90°＝∠BOF+∠COF∴∠EOB＝∠COF∴△BEO≌△CFO（ASA）∴BE＝CF＝3又∵AB＝BC∴AE＝BF＝4∴Rt△BEF中EF＝＝＝5．故选：C．9．如图，点E、F分别在矩形ABCD的边AB、BC上，且∠EFD＝90°，若BF＝3，BE＝4，CD＝9，则FC的长为（）A．12 B．13 C．14 D．15【答案】A【解答】解：∵∠EFD＝90°∴∠EFD＝∠B＝∠C＝90°∴∠EFB+∠DFC＝90°＝∠DFC+∠FDC∴∠EFB＝∠FDC∴△BEF∽△CFD∴∴∴CF＝12故选：A．二．填空题（共4小题）10．如图，矩形ABCD的对角线AC，BD相交于点O，过点O作OE⊥BD，交BC于点E，若，CE＝1，则BE的长为2．【答案】2．【解答】解：∵四边形ABCD是矩形∴OA＝OC，OB＝OD，AC＝BD，∠ABC＝90°∴∴，∠EBO＝∠ACB∵OE⊥BD∴∠BOE＝∠CBA＝90°∴△BOE∽△CBA∴即解得BE＝2或BE＝﹣3（舍去）故答案为：2．11．如图，在边长为2的正方形ABCD中E，F分别是边DC，CB上的动点，且始终满足DE＝CF，AE，DF交于点P，则∠APD的度数为90°；连接CP，线段CP的最小值为﹣1．【答案】90°，﹣1．【解答】解：∵四边形ABCD是正方形∴AD＝CD，∠ADE＝∠DCF＝90°在△ADE和△DCF中∴△ADE≌△DCF（SAS）∴∠DAE＝∠CDF∵∠CDF+∠ADF＝∠ADC＝90°∴∠ADF+∠DAE＝90°∴∠APD＝90°取AD的中点O，连接OP，则OP＝AD＝×2＝1（不变）根据两点之间线段最短得C、P、O三点共线时线段CP的值最小在Rt△COD中根据勾股定理得，CO＝＝＝所以，CP＝CO﹣OP＝﹣1．故答案为：90°，﹣1．12．如图，直线l过正方形ABCD的顶点B，点A、点C到直线l的距离分别为1和2，则正方形的边长是．【答案】见试题解答内容【解答】解：∵∠CBF+∠FCB＝90°∠CBF+∠ABE＝90°∴∠ABE＝∠FCB，同理∠BAE＝∠FBC∵AB＝BC∴△ABE≌△BCF（ASA）∴BE＝CF在直角△ABE中AE＝1，BE＝2∴AB＝．故答案为：．13．已知：如图，在长方形ABCD中AB＝4，AD＝6，延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，当点P运动1或7秒时，△ABP和△DCE全等．【答案】1或7．【解答】解：设点P运动t秒时，△ABP和△DCE全等．∵AB＝CD，∠ABP＝∠DCE＝90°，BP＝CE＝2，根据SAS证得△ABP≌△DCE由题意得：BP＝2t＝2∴t＝1∵AB＝CD，若∠BAP＝∠DCE＝90°，AP＝CE＝2，根据SAS证得△BAP≌△DCE由题意得：AP＝16﹣2t＝2解得t＝7．即当t的值为1或7秒时．△ABP和△DCE全等．故答案为：1或7．三．解答题（共3小题）14．如图，在四边形ABCD中∠BAC＝90°，E是BC的中点，AD∥BC，AE∥DC，EF⊥CD于点F．（1）求证：四边形AECD是菱形；（2）若AB＝6，AC＝8，求EF的长．【答案】（1）见解答；（2）．【解答】（1）证明：∵AD∥BC，AE∥DC∴四边形AECD是平行四边形∵∠BAC＝90°，E是BC的中点∴AE＝CE＝BC∴四边形AECD是菱形；（2）解：过A作AH⊥BC于点H，如图所示∵∠BAC＝90°，AB＝6，AC＝8∴BC＝＝10∵△ABC的面积＝BC×AH＝AB×AC∴AH＝＝∵点E是BC的中点，四边形AECD是菱形∴CD＝CE∵S▱AECD＝CE•AH＝CD•EF∴EF＝AH＝．15．如图所示，O是矩形ABCD的对角线的交点，DE∥AC，CE∥BD．（1）求证：OE⊥DC．（2）若∠AOD＝120°，DE＝2，求矩形ABCD的面积．【答案】见试题解答内容【解答】（1）证明：∵DE∥AC，CE∥BD∴DE∥OC，CE∥OD∴四边形ODEC是平行四边形∵四边形ABCD是矩形∴OD＝OC＝OA＝OB∴四边形ODEC是菱形∴OE⊥DC（2）∵DE＝2，且四边形ODEC是菱形∴OD＝OC＝DE＝2＝OA∴AC＝4∵∠AOD＝120，AO＝DO∴∠DAO＝30°，且∠ADC＝90°∴CD＝2，AD＝CD＝2∴S矩形ABCD＝2×2＝416．将两张长为8，宽为4的矩形纸片如图叠放．（1）判断四边形AGCH的形状，并说明理由；（2）求四边形AGCH的面积．【答案】（1）四边形AGCH是菱形，理由见解析过程；（2）20．【解答】解：（1）四边形AGCH是菱形，理由如下：∵四边形ABCD和四边形AFCE是矩形∴∠B＝∠F＝90°，AD∥BC，AF∥CE∴四边形AGCH是平行四边形∵S平行四边形AGCH＝GC•AB＝AG•CF，AB＝CF∴GC＝AG∴平行四边形AGCH是菱形；（2）由①可知，GC＝AG设GC＝AG＝x，则BG＝8﹣x在Rt△ABG中AB＝4由勾股定理得：42+（8﹣x）2＝x2解得：x＝5∴GC＝5∴S菱形AGCH＝GC•AB＝5×4＝20．一．选择题（共7小题）1．如图，在正方形ABCD中E、F分别是AB，BC的中点，CE，DF交于点G，连接AG，下列结论：①CE＝DF；②CE⊥DF；③∠AGE＝∠CDF；④∠EAG＝30°，其中正确的结论是（）A．①② B．①③ C．①②④ D．①②③【答案】D【解答】解：∵四边形ABCD是正方形∴AB＝BC＝CD＝AD，∠B＝∠BCD＝90°∵E，F分别是AB，BC的中点∴BE＝AB，CF＝BC∴BE＝CF在△CBE与△DCF中∴△CBE≌△DCF（SAS）∴∠ECB＝∠CDF，CE＝DF，故①正确；∵∠BCE+∠ECD＝90°∴∠ECD+∠CDF＝90°∴∠CGD＝90°∴CE⊥DF，故②正确；∴∠EGD＝90°延长CE交DA的延长线于H∵点E是AB的中点∴AE＝BE∵∠AHE＝∠BCE，∠AEH＝∠CEB，AE＝BE∴△AEH≌△BEC（AAS）∴BC＝AH＝AD∵AG是斜边的中线∴AG＝DH＝AD∴∠ADG＝∠AGD∵∠AGE+∠AGD＝90°，∠CDF+∠ADG＝90°∴∠AGE＝∠CDF．故③正确；∵CF＝BC＝CD∴∠CDF≠30°∴∠ADG≠60°∵AD＝AG∴△ADG不是等边三角形∴∠EAG≠30°，故④错误；故选：D．2．已知：如图，正方形ABCD中AB＝4，AC，BD相交于点O，E，F分别为边BC，CD上的动点（点E，F不与线段BC，CD的端点重合）且BE＝CF，连接OE，OF，EF．在点E，F运动的过程中有下列四个结论：①△OEF始终是等腰直角三角形；②△OEF面积的最小值是2；③至少存在一个△ECF，使得△ECF的周长是4+2；④四边形OECF的面积始终是4．所有正确结论的序号是（）A．①②③ B．③④ C．①②④ D．①②③④【答案】D【解答】解：①∵四边形ABCD是正方形，AC，BD相交于点O∴OB＝OC，∠OBC＝∠OCD＝45°在△OBE和△OCF中∴△OBE≌△OCF（SAS）∴OE＝OF∵∠BOE＝∠COF∴∠EOF＝∠BOC＝90°∴△OEF是等腰直角三角形；故①正确；②∵当OE⊥BC时，OE最小，此时OE＝OF＝BC＝2∴△OEF面积的最小值是×2×2＝2故②正确；③∵BE＝CF∴CE+CF＝CE+BE＝BC＝4假设存在一个△ECF，使得△ECF的周长是4+2则EF＝2由①得△OEF是等腰直角三角形∴OE＝＝．∵OB＝2，OE的最小值是2∴存在一个△ECF，使得△ECF的周长是4+2．故③正确；④由①知：△OBE≌△OCF∴S四边形OECF＝S△COE+S△OCF＝S△COE+S△OBE＝S△OBC＝S正方形ABCD＝×4×4＝4故④正确；故选：D．3．如图，正方形ABCD和长方形AEFG的面积相等，且四边形BEFH也是正方形，欧几里得在《几何原本》中利用该图得到了：BH2＝CH×GH．设AB＝a，CH＝b．若ab＝5，则图中阴影部分的周长是（）A．6 B．8 C．10 D．20【答案】C【解答】解：∵四边形ABCD，四边形BEFH为正方形，AB＝a，CH＝b∴BC＝AB＝CD＝a，BE＝BH＝EF＝BC﹣CH＝a﹣b，AE＝AB+BE＝a+a﹣b＝2a﹣b∴S正方形ABCD＝AB2＝a2S长方形AEFG＝AE•EF＝（2a﹣b）（a﹣b）＝2a2﹣3ab+b2∵正方形ABCD和长方形AEFG的面积相等∴a2＝2a2﹣3ab+b2整理得：a2+b2＝3ab∴（a+b）2＝5ab∵ab＝5∴（a+b）2＝5×5∴a+b＝5∴阴影部分的周长为：2（CD+CH）＝2（a+b）＝10．故选：C．4．如图，在正方形ABCD中AB＝4，E，F分别为边AB，BC的中点，连接AF，DE，点G，H分别为DE，AF的中点，连接GH，则GH的长为（）A． B．1 C． D．2【答案】C【解答】解：连接AG并延长交CD于M，连接FM∵四边形ABCD是正方形∴AB＝CD＝BC＝4，AB∥CD，∠C＝90°∴∠AEG＝∠GDM，∠EAG＝∠DMG∵G为DE的中点∴GE＝GD在△AGE和MGD中∴△AGE≌△MGD（AAS）∴AG＝MG，AE＝DM＝AB＝CD∴CM＝CD＝2∵点H为AF的中点∴GH＝FM∵F为BC的中点∴CF＝BC＝2∴FM＝＝2∴GH＝故选：C．5．如图，正方形ABCD和正方形CEFG中点D在CG上，已知BC＝1，CE＝7，点H是AF的中点，则CH的长是（）A．5 B．3.5 C．4 D．【答案】A【解答】解：∵正方形ABCD和正方形CEFG中点D在CG上，BC＝1，CE＝7∴AB＝BC＝1，CE＝EF＝7，∠E＝90°延长AD交EF于M，连接AC、CF则AM＝BC+CE＝1+7＝8，FM＝EF﹣AB＝7﹣1＝6，∠AMF＝90°∵四边形ABCD和四边形GCEF是正方形∴∠ACD＝∠GCF＝45°∴∠ACF＝90°∵H为AF的中点∴CH＝AF在Rt△AMF中由勾股定理得：AF＝＝＝10∴CH＝5故选：A．6．如图，在矩形ABCD中AB＝2，AD＝1，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2 B．4 C． D．2【答案】C【解答】解：如图：当点F与点C重合时，点P在P1处，CP1＝DP1当点F与点E重合时，点P在P2处，EP2＝DP2∴P1P2∥CE且P1P2＝CE．当点F在EC上除点C、E的位置处时，有DP＝FP．由中位线定理可知：P1P∥CE且P1P＝CF．∴点P的运动轨迹是线段P1P2∴当BP⊥P1P2时，PB取得最小值．∵矩形ABCD中AB＝2，AD＝1，E为AB的中点∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝1．∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°．∴∠DP2P1＝90°．∴∠DP1P2＝45°．∴∠P2P1B＝90°，即BP1⊥P1P2∴BP的最小值为BP1的长．在等腰直角BCP1中CP1＝BC＝1．∴BP1＝．∴PB的最小值是．故选：C．7．如图，▱ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC＝60°，AB＝BC，连接OE，下列结论：①∠CAD＝30°；②OD＝AB；③S▱ABCD＝AC•CD；④S四边形OECD＝S△AOD，其中成立的个数为（）A．1个 B．2个 C．3个 D．4个【答案】见试题解答内容【解答】解：∵四边形ABCD为平行四边形，∠ADC＝60°∴AD∥BC，∠ABC＝∠ADC＝60°，OB＝OD∴∠DAE＝∠AEB，∠BAD＝∠BCD＝120°∵AE平分∠BAD∴∠BAE＝∠DAE∴∠BAE＝∠AEB∴△ABE为等边三角形∴∠BAE＝∠AEB＝60°，AB＝BE＝AE∵AB＝BC∴EC＝AE∴∠EAC＝∠ECA＝30°∴∠CAD＝30°，故①正确；∵∠BAD＝120°，∠CAD＝30°∴∠BAC＝90°∴BO＞AB∴OD＞AB，故②错误；∴S▱ABCD＝AB•AC＝AC•CD，故③正确；∵∠BAC＝90°，BC＝2AB∴E是BC的中点∴S△BEO：S△BCD＝1：4∴S四边形OECD：S△BCD＝3：4∴S四边形OECD：S▱ABCD＝3：8∵S△AOD：S▱ABCD＝1：4∴S四边形OECD＝S△AOD，故④正确．故选：C．二．填空题（共5小题）8．如图，在正方形ABCD中AB＝3cm，延长BC到点E，使CE＝1cm，连接DE，动点P从点A出发，以每秒1cm的速度沿AB→BC→CD→DA向终点A运动．设点P的运动时间为t秒，当△PBC和△DCE全等时，t的值为2或7．【答案】2或7．【解答】解：∵△DCE是直角三角形∴△PBC为直角三角形∴点P只能在AB上或者CD上当点P在AB上时，有BP＝CE∴BP＝CE＝1∴AP＝2∴t＝2÷1＝2当点P在CD上时，有CP＝CE＝1∴t＝（3+3+1）÷1＝7故答案为：2或7．9．如图，在菱形ABCD中∠B＝45°，E、F分别是边CD，BC上的动点，连接AE、EF，G、H分别为AE、EF的中点，连接GH．若GH的最小值为3，则BC的长为．【答案】．【解答】解：连接AF∵G，H分别为AE，EF的中点∴GH∥AF，且要使GH最小，只要AF最小当AF⊥BC时，AF最小∵GH的最小值为3∴AF＝6∵∠B＝45°∴∠BAF＝45°∴BF＝AF＝6∴∵四边形ABCD是菱形∴．故答案为：．10．如图，在菱形ABCD中对角线AC，BD交于点O，点E为AB的中点，点F在OD上，DF＝OF，连接EF交OA于点G，若OG＝1，连接CE，S△BEC＝12，则线段CE的长为3．【答案】3．【解答】解：作EM⊥OA于M∵四边形ABCD是菱形∴BD⊥OA，OD＝OB，OA＝OC∴EM∥OB∴AM：MO＝AE：EB∵AE＝BE∴AM＝OM∴EM是△ABO的中位线∴EM＝∵DF＝OF∴OF＝OD∴EM＝OF∵∠MEG＝∠OFG，∠MGE＝∠OGF∴△EMG≌△FOG（AAS）∴MG＝OG＝1∴OM＝2OG＝2∴OA＝2OM＝4∴AC＝2OA＝8∵AE＝BE∴△BAC的面积＝2×△BEC的面积＝2×12＝24∴AC•OB＝24∴OB＝6∴EM＝OB＝3∵CM＝OM+OC＝2+4＝6∴CE＝＝3．故答案为：3．11．如图，在平面直角坐标系中矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC边上运动，点Q是坐标平面内的任意一点．若以O，D，P，Q为顶点的四边形是边长为5的菱形时，则点Q的坐标为（﹣3，4）或（8，4）或（3，4）．【答案】（﹣3，4）或（8，4）或（3，4）．【解答】解：∵A（10，0），C（0，4）∴OC＝AB＝4，BC＝OA＝10∵点D是OA的中点∴OD＝5①如图1所示，以OP为对角线，点P在点D的左侧时，PD＝OD＝5过点P作PE⊥x轴于点E，则PE＝OC＝4．在Rt△PDE中由勾股定理得：∴OE＝OD﹣DE＝5﹣3＝2∴点P的坐标为（2，4）此时，点Q的坐标为（﹣3，4）；②如图2所示，以OQ为对角线，点P在点D的左侧时，OP＝OD＝5．过点P作PE⊥x轴于点E，则PE＝4．在Rt△POE中由勾股定理得：∴点P的坐标为（3，4）此时，点Q的坐标为（8，4）；③如图3所示，以OP为对角线，点P在点D的右侧时，PD＝OD＝5过点P作PE⊥x轴于点E，则PE＝4．在Rt△PDE中由勾股定理得：∴OE＝OD+DE＝5+3＝8∴点P的坐标为（8，4）此时，点Q的坐标为（3，4）；综上所述，点Q的坐标为（﹣3，4）或（8，4）或（3，4）；故答案为：（﹣3，4）或（8，4）或（3，4）．12．如图，在△ABC中∠C＝90°，AC＝6，BC＝8，点D在AB边上，DE⊥AC，DF⊥BC，垂足分别为点E、F，连接EF，则线段EF的最小值等于4.8．【答案】4.8．【解答】解：如图，连接CD．∵∠ACB＝90°，AC＝6，BC＝8∴AB＝＝10∵DE⊥AC，DF⊥BC，∠ACB＝90°∴四边形CFDE是矩形∴EF＝CD由垂线段最短可得CD⊥AB时，线段EF的值最小∵S△ABC＝BC•AC＝AB•CD∴×8×6＝×10×CD解得CD＝4.8∴EF＝4.8．故答案为：4.8．三．解答题（共5小题）13．【问题情境】：如图1，点E为正方形ABCD内一点，AE＝2，BE＝4，∠AEB＝90°，将直角三角形ABE绕点A逆时针方向旋转α度（0≤α≤180°）点B、E的对应点分别为点B′、E′．【问题解决】：（1）如图2，在旋转的过程中点B′落在了AC上，求此时CB′的长；（2）若α＝90°，如图3，得到△ADE′（此时B′与D重合），延长BE交DE′于点F①试判断四边形AEFE′的形状，并说明理由；②连接CE，求CE的长；（3）在直角三角形ABE绕点A逆时针方向旋转过程中直接写出线段CE′长度的取值范围．【答案】（1）2﹣2；（2）①正方形，理由见解析；②2；（3）2≤CE'≤2+2．【解答】解：（1）∵AE＝2，BE＝4，∠AEB＝90°∴AB＝＝＝2∵四边形ABD是正方形∴BC＝AB＝2，∠ABC＝90°∴AC＝AB＝2由旋转的性质得：AB'＝AB＝2∴CB′＝AC﹣AB'＝2﹣2；（2）①四边形AEFE′是正方形，理由如下：由旋转的性质得：AE'＝AE，∠EAE'＝α＝90°，∠AE'D＝∠AEB＝90°∵∠AEF＝180°﹣90°＝90°∴四边形AEFE′是矩形又∵AE'＝AE∴四边形AEFE′是正方形；②过点C作CG⊥BE于点G，如图3所示：则∠BGC＝90°＝∠AEB∴∠CBG+∠BCG＝∠CBG+∠ABE＝90°∴∠BCG＝∠ABE在△BCG和△ABE中∴△BCG≌△ABE（AAS）∴CG＝BE＝4，BG＝AE＝2∴EG＝BE﹣BG＝4﹣2＝2∴CE＝＝＝2；（3）∵直角三角形ABE绕点A逆时针方向旋转α度（0≤α≤180°）点B、E的对应点分别为点B′、E′∴当α＝0°时，E'与E重合，CE'最短＝2；当E'落在CA的延长线上时，AE'＝AE＝2，CE'最长＝AC+AE'＝2+2∴线段CE′长度的取值范围是2≤CE'≤2+2．14．已知：如图（1），在平面直角坐标系中点A、点B分别在x轴、y轴的正半轴上，点C在第一象限，∠ACB＝90°，AC＝BC，点A坐标为（m，0），点C横坐标为n，且m2+n2﹣2m﹣8n+17＝0．（1）分别求出点A、点B、点C的坐标；（2）如图（2），点D为边AB中点，以点D为顶点的直角∠EDF两边分别交边BC于E，交边AC于F，①求证：DE＝DF；②求证：S四边形DECF＝S△ABC；（3）在坐标平面内有点G（点G不与点A重合），使得△BCG是以BC为直角边的等腰直角三角形，请直接写出满足条件的点G的坐标．【答案】见试题解答内容【解答】解：（1）∵m2+n2﹣2m﹣8n+17＝0．∴（m﹣1）2+（n﹣4）2＝0∴m＝1，n＝4∴点A（1，0），CM＝4如图（1），过点C作CM⊥OB，CN⊥OA∵CM⊥OB，CN⊥OA，∠AOB＝90°∴四边形OMCN是矩形∴∠MCN＝90°＝∠ACB，CM＝ON＝4，CN＝OM∴AN＝3∴∠BCM＝∠ACN，且AC＝BC，∠BMC＝∠ANC∴△BCM≌△ACN（AAS）∴CM＝CN＝4＝OM，AN＝BM＝3∴点B（0，7），点C（4，4）；（2）①如图（2），连接CD∵AC＝BC，∠ACB＝90°，点D为边AB中点∴BD＝CD＝AD，∠ABC＝∠BAC＝∠BCD＝∠ACD＝45°，AB⊥CD∵∠EDF＝90°＝∠BDC∴∠BDE＝∠CDF，且BD＝CD，∠ABC＝∠DCA∴△BDE≌△CDF（AAS）∴DE＝DF②∵△BDE≌△CDF∴S△BDE＝S△CDF∴S△BDE+S△EDC＝S△CDF+S△EDC∴S△BDC＝S四边形EDFC∵AD＝BD∴S△BDC＝S△ABC∴S四边形DECF＝S△ABC；（3）如图（3）若∠GBC＝90°，BG＝BC时，且点G在BC下方，过点G作GF⊥OB，过点C作CE⊥OB∵∠GBF+∠EBC＝90°，∠GBF+∠BGF＝90°∴∠EBC＝∠BGF，且∠BEC＝∠BFG＝90°，BG＝BC∴△BGF≌△CBE（AAS）∴BF＝CE＝4，GF＝BE∴OF＝3∴点G（﹣3，3）若∠GBC＝90°，BG＝BC时，且点G在BC上方同理可求点G（3，11）若∠GCB＝90°，CG＝BC时，点G在BC上方同理可求点G（7，8）15．综合与实践：【思考尝试】（1）数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中E是边AB上一点，DF⊥CE于点F，GD⊥DF，AG⊥DG，AG＝CF，试猜想四边形ABCD的形状，并说明理由；【实践探究】（2）小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD中E是边AB上一点，DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G，可以用等式表示线段FH，AH，CF的数量关系，请你思考并解答这个问题；【拓展迁移】（3）小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中E是边AB上一点，AH⊥CE于点H，点M在CH上，且AH＝HM，连接AM，BH，可以用等式表示线段CM，BH的数量关系，请你思考并解答这个问题．【答案】见试题解答内容【解答】解：（1）四边形ABCD是正方形理由：∵四边形ABCD是矩形∴∠ADC＝90°∵GD⊥DF∴∠FDG＝90°∴∠ADG＝∠CDF又∵AG＝CF，∠G＝∠DFC＝90°∴△ADG≌△CDF（AAS）∴AD＝CD∴四边形ABCD是正方形；（2）HF＝AH+CF理由：∵DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G∴四边形HFDG是矩形∴∠G＝∠DFC＝90°∵四边形ABCD是正方形∴AD＝CD，∠ADC＝90°∴∠ADG＝∠CDF∴△ADG≌△CDF（AAS）∴AG＝CF，DG＝DF∴矩形HFDG是正方形∴HG＝HF＝AH+AG＝AH+CF；（3）连接AC，如图∵四边形ABCD是正方形，∴∠BAC＝45°∵AH⊥CE，AH＝HM∴△AHM是等腰直角三角形∴∠HAM＝45°∴∠HAB＝∠MAC∵∴△AHB∽△AMC∴即BH＝CM．16．回答问题（1）【初步探索】如图1，在四边形ABCD中AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系，小王同学探究此问题的方法是：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论是∠BAE+∠FAD＝∠EAF；（2）【灵活运用】如图2，若在四边形ABCD中AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】已知在四边形ABCD中∠ABC+∠ADC＝180°，AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3，仍然满足EF＝BE+FD，请直接写出∠EAF与∠DAB的数量关系．【答案】见试题解答内容【解答】解：（1）结论：∠BAE+∠FAD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴∠BAE＝∠DAG，AE＝AG∵EF＝BE+DF∴EF＝DF+DG＝FG在△AEF和△AGF中∴△AEF≌△AGF（SSS）∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠FAD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°∴∠B＝∠ADG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴∠BAE＝∠DAG，AE＝AG在△AEF和△AGF中∴△AEF≌△AGF（SSS）∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）结论：∠EAF＝180°﹣∠DAB．理由：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°∴∠ADC＝∠ABE在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AG＝AE，∠DAG＝∠BAE在△AEF和△AGF中∴△AEF≌△AGF（SSS）∴∠FAE＝∠FAG∵∠FAE+∠FAG+∠GAE＝360°∴2∠FAE+（∠GAB+∠BAE）＝360°∴2∠FAE+（∠GAB+∠DAG）＝360°即2∠FAE+∠DAB＝360°∴∠EAF＝180°﹣∠DAB．17．（1）如图1，在正方形ABCD中点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则的值为1；（2）如图2，在矩形ABCD中AD＝5，CD＝3，点E是AD上的一点，连接CE，BD，且CE⊥BD，则的值为；（3）如图3，在四边形ABCD中∠A＝∠B＝90°，点E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：；（4）如图4，在Rt△ABD中∠BAD＝90°，AB＝3，AD＝9，将△ABD沿BD翻折，点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．请问．是定值吗？若是，直接写出这个定值，若不是，请说明理由．【答案】（1）1；（2）；（3）见解析；（4）是定值．【解答】（1）解：∵四边形ABCD是正方形∴AD＝DC，∠A＝∠FDC＝90°∵DE⊥CF∴∠ADE+∠DFC＝90°，∠DFC+∠DCF＝90°∴∠ADE＝∠DCF在△ADE与△DCF中∴△ADE≌△DCF（ASA）∴DE＝CF∴故答案为：1；（2）解：∵四边形ABCD为矩形∴∠A＝∠EDC＝90°∵CE⊥BD∴∠ADB+∠CED＝90°，∠CED+∠DCE＝90°∴∠ADB＝∠DCE∴△ADB∽△DCE∴故答案为：；（3）证明：如图，过点作CH⊥AD，交AD延长线于H∵∠H＝∠A＝∠B＝90°∴四边形ABCH为矩形∴CH＝AB∵CG⊥EG∴∠G＝90°＝∠A＝∠H∵∠ADE＝∠GDF∵∠GFD＝∠HFC∴∠ADE＝∠HCF∴△ADE∽△HCF∴；（4）解：是定值，理由如下：连接AC交BD于H，CF与DE交于G，CF与DB交于P∵将△ABD沿BD翻折，点A落在点C处得△CBD∴AC⊥BD∴∠BAH+∠CAF＝90°，∠BAH+∠EBD＝90°，∠CHP＝90°∴∠CAF＝∠DBE∵CF⊥DE∴∠PGD＝90°＝∠CHP∵∠HPC＝∠GPD∴∠ACF＝∠BDE∴△ACF∽△BDE∴∵AB＝3，AD＝9由勾股定理得BD＝＝3∴∴AH＝∴AC＝2AH＝∴1．（2023•湘潭）如图，菱形ABCD中连接AC，BD，若∠1＝20°，则∠2的度数为（）A．20° B．60° C．70° D．80°【答案】C【解答】解：∵四边形ABCD是菱形∴AB∥CD，AC⊥BD∴∠DCA＝∠1＝20°∴∠2＝90°﹣∠DCA＝70°故选：C．2．（2023•内蒙古）如图，在菱形ABCD中AB＝4，∠A＝120°，顺次连接菱形ABCD各边中点E、F、G、H，则四边形EFGH的周长为（）A．4+2 B．6+2 C．4+4 D．6+4【答案】C【解答】解：连接AC、BD交于O∵四边形ABCD是菱形，∠BAD＝120°∴∠ABC＝60°∵AB＝BC∴△ABC是等边三角形∴AC＝AB＝4∵∠AO