新教材2023-2024学年高中数学第6章平面向量初步6.3平面向量线性运算的应用分层作业新人教B版必修第二册

第六章6.3平面向量线性运算的应用A级必备知识基础练1.[探究点一](多选题)若O是△ABC所在平面内一点,且满足|OB-OC|=|OB+OC-2OA|,则△ABCA.钝角三角形 B.直角三角形C.等腰直角三角形 D.等边三角形2.[探究点二·2023陕西榆林高一]某学生做引体向上运动,处于如图所示的平衡状态时,若两只胳膊的夹角为60°,每只胳膊的拉力大小均为500N,则该学生的体重m(单位:kg)约为()(参考数据:重力加速度大小g取10m/s2,3≈1.732)A.81 B.87 C.89 D.913.[探究点一]△ABC所在平面内一点P满足PA+PC=mAB(m>0,m为常数),若△ABP的面积为6,则△ABC的面积为4.[探究点二]在静水中划船速度的大小是每分钟40m,水流速度的大小是每分钟20m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,那么小船的行进方向应指向哪里?B级关键能力提升练5.已知O是平面内的一定点,A,B,C是平面内不共线的三个动点,若动点P满足OP=OA+λ(AB+AC),λ∈(0,+∞),则点P的轨迹一定通过△ABCA.内心 B.外心 C.重心 D.垂心6.P是△ABC所在平面内一点,满足|CB|-|PB+PC-2PA|=0,则△ABC的形状是(A.钝角三角形 B.直角三角形C.等腰三角形 D.等边三角形7.(多选题)在△ABC中,D,E,F分别是边BC,CA,AB的中点,点G为△ABC的重心,则下述结论正确的是()A.ABB.AG=C.AF+BDD.GA+GB8.如图,在直角梯形ABCD中,AB∥DC,AD⊥DC,AD=DC=2AB,E为AD的中点,若CA=λCE+μDB,则λ=,μ=.

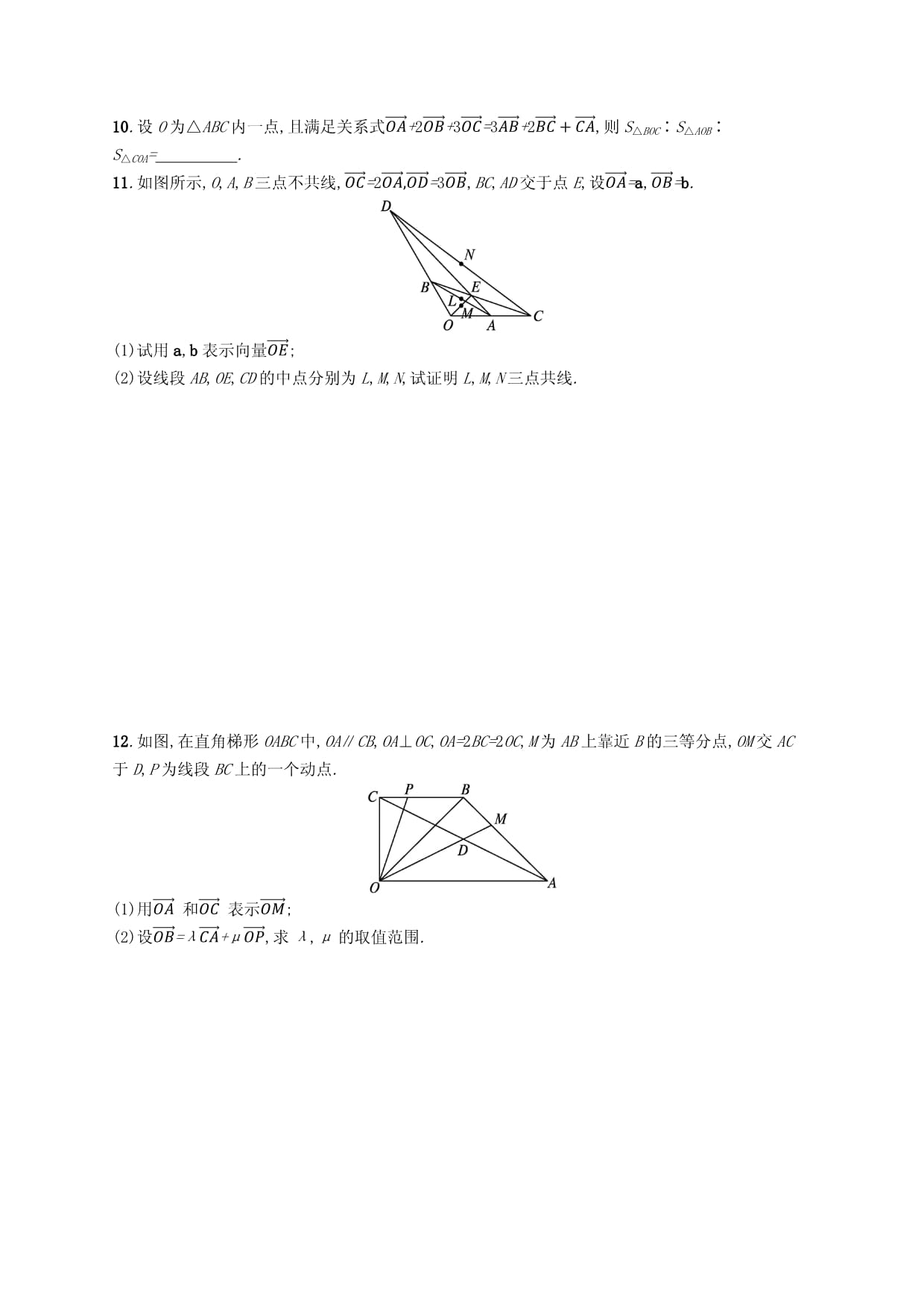
9.在△ABC中,点D和E分别在BC,AC上,且BD=13BC,CE=13CA,C级学科素养创新练10.设O为△ABC内一点,且满足关系式OA+2OB+3OC=3AB+2BC+CA,则S△BOC∶S△AOB∶S△COA=11.如图所示,O,A,B三点不共线,OC=2OA,OD=3OB,BC,AD交于点E,设OA=a,OB=(1)试用a,b表示向量OE;(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.12.如图,在直角梯形OABC中,OA∥CB,OA⊥OC,OA=2BC=2OC,M为AB上靠近B的三等分点,OM交AC于D,P为线段BC上的一个动点.(1)用OA和OC表示OM;(2)设OB=λCA+μOP,求λ,μ的取值范围.

参考答案6.3平面向量线性运算的应用1.AD设点M为BC边的中点,由题意可得|OB-OC|=|CB|OB+OC-2OA|=|2OM-2OA|=2|AM据此结合题意可知CB=2AM,由三角形的性质可知,△ABC的形状是直角三角形.故选AD.2.B设两只胳膊的拉力分别为F1,F2,则|F1|=|F2|=500,<F1,F2>=60°,∴|F1+F2|=(F1+F∴10m=866,解得m=86.6≈87.∴学生的体重约为87kg.故选B.3.12取AC的中点O,∵PA+PC=mAB(m>0,m∴mAB=2PO,∴点C到直线AB的距离等于点P到直线AB的距离的2倍,∴S△ABC=2S△ABP=12.4.解如图所示,设向量OA的长度和方向表示水流速度的大小和方向,向量OB的长度和方向表示船在静水中速度的大小和方向,以OA,OB为邻边作平行四边形OACB,连接OC.依题意OC⊥OA,BC=OA=20,OB=40,∴∠BOC=30°.故小船应向上游(左)与河岸夹角为60°的方向行进.5.C由题意,得OP-OA=λ(AB+AC),即AP=λ(AB+AC),根据平行四边形法则,知AB+AC是△ABC的中线AD(D为BC的中点)所对应向量AD的2倍6.B由|CB|=|PB+PC-2PA|,可得|CB|=|AB+AC|,即|AB所以四边形ABCD为矩形,因此,△ABC是直角三角形.故选B.7.CDAB+BC=AC≠12(AB+AC)=ADAF+BD+CE=12(GA+GB+GC=-2312(AB+AC)+12(BA+故选CD.8.6525以D为原点,DC边所在直线为x轴,DA不妨设AB=1,则D(0,0),C(2,0),A(0,2),B(1,2),E(0,1),∴CA=(-2,2),CE=(-2,1),DB=(1,2).∵CA=λCE+μDB,∴(-2,2)=λ(-2,1)+μ(1,2),∴-2λ9.证明由A,D,R三点共线,可得CR=λCD+(1-λ)CA=23λCB+(1由B,E,R三点共线,可得CR=μCB+(1-μ)CE=μCB+13(1-μ)CA∴CR=∴AD=CD-CA=23CB-CA10.3∶2∶1∵OA+2OB+3OC=3AB+2BC+CA=3(OB-OA)+2(OC-∴3OA+OB+2OC=∴OA+OB+2OC+2OA=分别取AB,AC的中点为D,E,则OD=2EO,点O为线段DE的三等分点(靠近点E).延长AO交BC于点F,∴S△AOB=12S△ABF=12×23S△ABC=S△AOC=12S△ACF=12×13S△ABC=S△BOC=12S△ABC∴S△BOC∶S△AOB∶S△COA=12S△ABC∶13S△ABC∶16S△ABC=3∶211.(1)解∵B,E,C三点共线,∴令OE=xOC+(1-x)OB=2xa+(1-x)b,①同理,∵A,E,D三点共线,令OE=yOA+(1-y)OD可得OE=ya+3(1-y)b,②由①②,得2x=∴OE=45a+(2)证明∵OL=a+b∴MN=∴MN=6ML.又MN与ML交于点M,∴L,M,N12.解(1)因为M为AB上靠近B的三等分点,所以MA=2又CB∥OA,且CB=12OA,所以CB则OM=OA-MA=OA-23(OA-OB(2)根据题意,因为OA⊥OC,故以O为坐标原点,建立如图所示平面直角坐标系:设OA=2,则A(2,0),C(0,1),B(1,1),O(0,0