运筹学课件-对偶问题

Chapter2对偶问题DualProblem1.线性规划的对偶模型

DualModelofLP2.对偶性质

Dualproperty3.对偶单纯形法

DualSimplexMethod4.灵敏度分析

SensitivityAnalysis运筹学OperationsResearch

在线性规划问题中，存在一个有趣的问题，即每一个线性规划问题都伴随有另一个线性规划问题，称它为对偶线性规划问题。对偶问题是对原问题从另一角度进行的描述，其最优解与原问题的最优解有着密切的联系，在求得一个线性规划问题最优解的同时也就得到其对偶线性规划的最优解，反之也然。对偶理论就是研究线性规划及其对偶问题的理论，是线性规划理论的重要内容之一。2.1对偶理论

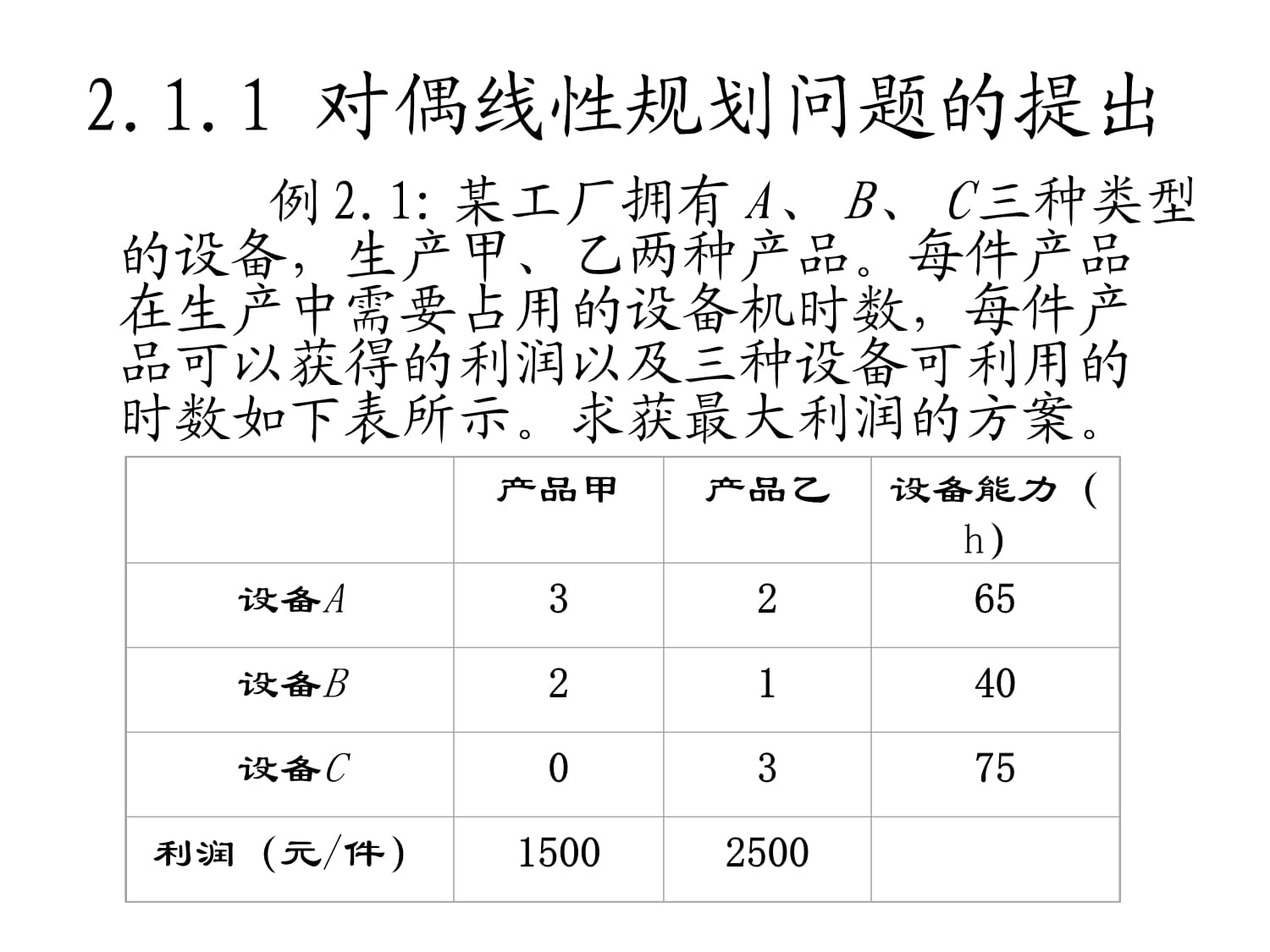
例2.1:某工厂拥有A、B、C三种类型的设备，生产甲、乙两种产品。每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备可利用的时数如下表所示。求获最大利润的方案。2.1.1对偶线性规划问题的提出

产品甲产品乙设备能力（h）设备A3265设备B2140设备C0375利润（元/件）15002500

解】设x1，x2分别为产品甲，乙的产量，则线性规划数学模型为：

现在从另一个角度来考虑企业的决策问题。假如企业自己不生产产品，而将现有的资源转让或出租给其它企业，那么资源的转让价格是多少才合理？价格太高对方不愿意接受，价格太低本单位收益又太少。合理的价格应是对方用最少的资金购买本企业的全部资源，而本企业所获得的利润不应低于自己用于生产时所获得的利润。这一决策问题应考虑这样几个方面。（1）出卖资源获利应不少于生产产品的获利。即出卖能够制造一件产品的设备所获得的收入应该不少于生产一件该产品所获得的收入。

（2）价格应尽量低，这样才能有竞争力。（如果客户肯以更高的价格购买，则企业获得的利润更多，因此这样制定出的价格可以作为谈判中的低价，但不一定是实际成交的价格。）

（3）价格应该是非负的。

若以分别表示三种设备的出售价格，则第一条要求可以表示为:3y1+2y2≥1500生产一件产品甲的设备的销售收入应该不少于不少于甲产品的利润.

2y1+y2+3y3≥2500生产一件产品甲的设备的销售收入应该不少于不少于甲产品的利润.出售所有设备所获得的总收入为:65y1+40y2+75y3

Maxz=1500x1+2500x2

s.t.3x1+2x2≤65

2x1+x2≤40原问题

3x2≤75

x1,x2≥0

由此有:

Minf=65y1+40y2+75y3

s.t.3y1+2y2≥1500

（不少于甲产品的利润）

2y1+y2+3y3≥2500对偶问题

（不少于乙产品的利润）

y1,y2,y3≥0

上述两个线性规划模型是在同一企业的资源状况和生产技术条件下产生的，是同一问题从不同角度来观察所产生的。我们称这两个线性规划问题为互为对偶的两个线性规划问题。其中一个问题是另一个问题的对偶问题。2.1.2对偶问题的定义对于线性规划问题：(1)我们称(2)是（1）的对偶问题，也称（1）是（2）的对偶问题。这种对偶关系称为对称形式的对偶关系，用矩阵可以表示为：对称形式的对偶问题的特点为:(1)若原问题目标是求极大化,则对偶问题的目标是极小化,反之也然.原问题的目标函数系数成为对偶问题的右端常数,其右端常数成为对偶问题的目标函数系数.(2)原问题的约束系数矩阵与对偶问题的约束系数矩阵互为转置矩阵。

（3）极大化问题的每个约束对应于极小化问题的一个变量，其每个变量对应于对偶问题的一个约束。极大化问题的每个约束为的形式，对应于极小化问题的变量。极大化问题的变量，对应于极小化问题的约束为的形式。【例2.2】写出下列线性规划的对偶问题【解】这是一个对称形式的线性规划，它的对偶问题求最小值，有三个变量且非负，有两个“≥”约束，即【例2.3】写出下列线性规划的对偶问题【解】这是一个对称形式的线性规划，设Y=（y1，y2），则有从而对偶问题为对偶变量yi也可写成xi的形式。

对于一般的线性规划问题，也可以定义其对偶线性规划问题。具体的定义方法如下：

称（22）是（21）的对偶问题，也称（21）是（22）的对偶问题。将上述原问题与对偶问题的对应关系列于表2－1

原问题（或对偶问题）

对偶问题（或原问题）目标函数（maxZ）目标函数系数（资源限量）约束条件系数矩阵A（AT）目标函数（minW）资源限量（目标函数系数）约束条件系数矩阵ATA）变

量n个变量第j个变量≥0第j

个变量≤0第j个变量无约束约

束n个约束第j个约束为≥第j

个约束为≤第j个约束为=约

束m个约束第i个约束≤第i个约束≥第i个约束为=变

量m个变量第i个变量≥0第i个变量≤0第i个变量无约束

表2－1例如，原问题是求最小值，按表2-1有下列关系：

1.第i个约束是“≤”约束时，第i个对偶变量yj≤02．第i个约束是“=”约束时，第i个对偶变量yi无约束；3．当xj≤0时，第j个对偶约束为“≥”约束，当xj无约束时，第j个对偶约束为“=”约束。

其中若原问题是极大化问题，则按表格从左往右查，若原问题是极小化问题，则按表格从右往左查。【例2.4】写出此线性规划的对偶问题

【解】目标函数求最小值，应将表2－1