郑州轻工业大学概率论与数理统计课件-第1-4讲

第1讲

绪

论徐雅静主讲郑州轻工业大学1.客观世界中的两类现象两类现象:必然现象和随机现象.一定条件下必然发生的现象,称为必然现象;在标准大气压下,

100 C的纯水必然沸腾;向上抛一枚石子必然下落;电荷同性相斥,异性相吸…“概率论与数理统计”绪论1.客观世界中的两类现象两类现象:必然现象和随机现象.一定条件下必然发生的现象,称为必然现象.·

很多课程主要内容就是研究必然现象中的数量规律性的.2,12如

s=

=2

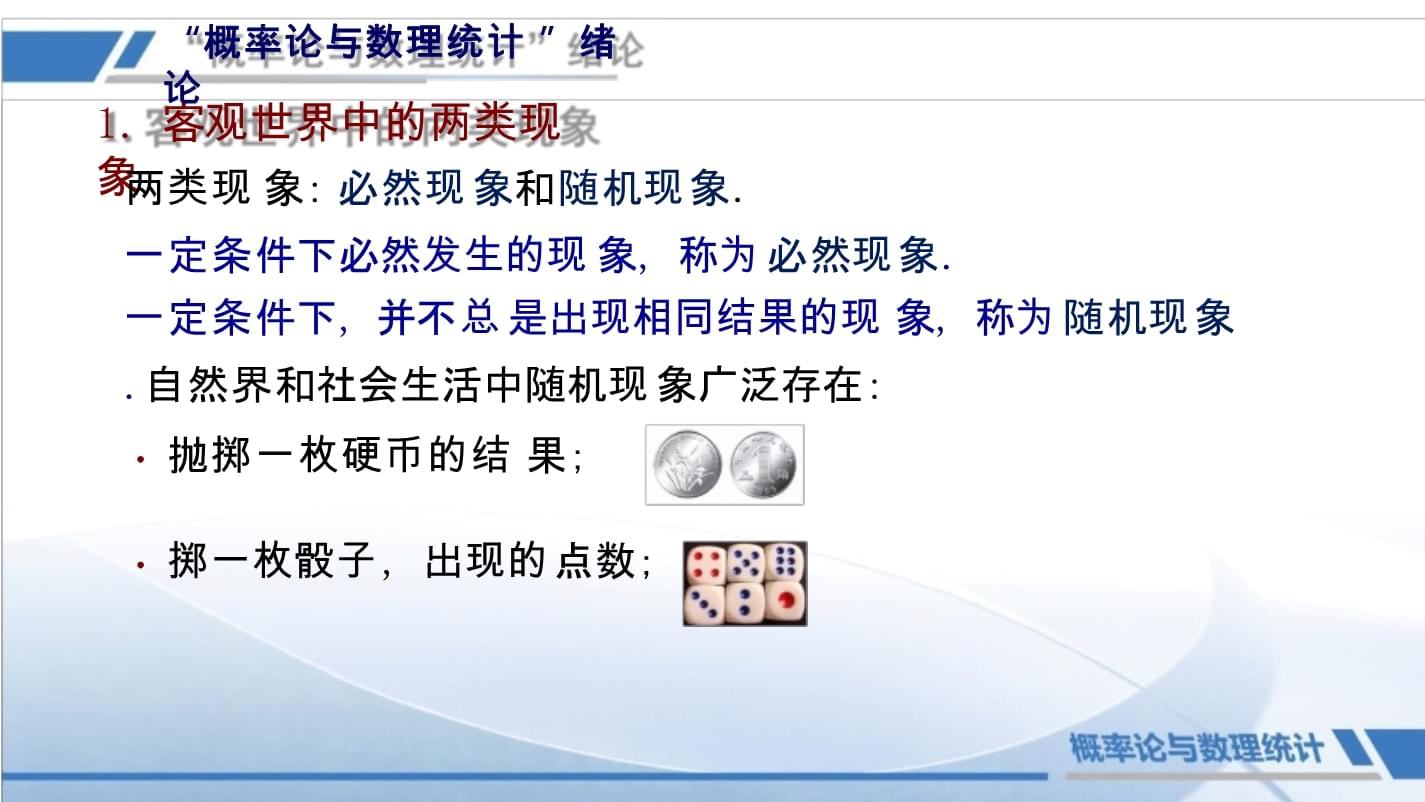
…“概率论与数理统计”绪论1.客观世界中的两类现象两类现象:必然现象和随机现象.一定条件下必然发生的现象,称为必然现象.一定条件下,并不总是出现相同结果的现象,称为随机现象.自然界和社会生活中随机现象广泛存在:抛掷一枚硬币的结果;掷一枚骰子,出现的点数;“概率论与数理统计”绪论1.客观世界中的两类现象两类现象:必然现象和随机现象.自然界和社会生活中随机现象广泛存在:抛掷一枚硬币,哪一面朝上;掷一枚骰子,出现的点数;某超市一天的客流量;“概率论与数理统计”绪论1.客观世界中的两类现象两类现象:必然现象和随机现象.自然界和社会生活中随机现象广泛存在:明天的天气情况;某品牌电视机的寿命;明天股市的涨跌;“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性随机现象的随机性或不确定性,困扰了人类很长时间.在面临不确定性时,人们往往依赖于像占星术、占卜之类的伪科学来作出决策.“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性随机现象是杂乱无章不可把握的吗?人面们对逐随渐机发问现题所人谓类的应随如机何性做,只出是决对策一?次或少数几次观察而言;

当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.·

多次重复抛一枚硬币得到正面朝上大致有一半;“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.·

大量的调查发现在自然人群中男性和女性大致各占一半;“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.·连续考察若干年发现某地区的年均降雨量在某一个较小范围内变化;“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.·

大量试验后发现某品牌电视机的寿命集中在某个区间内;…….“概率论与数理统计”绪论2.随机现象的不确定性与统计规律性当在相同条件下进行大量观察时,随机现象呈现出一定的规律性.·某超市对大量顾客的购物篮观察发现:啤酒和尿布放在一起很好卖;“概率论与数理统计”绪论3.概率论与数理统计的产生在公元17世纪前后,人们就开始对随机现象进行思考、研究.随着时间的推移和研究的深入,一些概率论的基本概念逐渐被提出;“概率论与数理统计”绪论3.概率论与数理统计的产生“概率论与数理统计”绪论17世纪中期,惠更斯发表的《论赌博中的计算》标志着概率论的诞生.克里斯蒂安·惠更斯(ChristiaanHuygens;

1629.4—1695.7),荷兰物理学家、天文学家、数学家，他是介于伽利略与牛顿之间一位重要的物理学先驱，是历史上最著名的物理学家之一，他在力学、光学、数学和天文学方面都有卓越的成就和杰出的贡献.3.概率论与数理统计的产生随着概率论的诞生,人们又逐渐尝试用数学方法来研究随机现象,从而发展了研究随机现象规律性的学科——“概率论与数理统计”.近代的“概率论与数理统计”理论形成于20世纪初期.“概率论与数理统计”绪论3.概率论与数理统计的产生“概率论与数理统计”分两部分:“概率论”和“数理统计”.“概率论”是从数量化的角度研究随机现象规律性的一门数学分支.

“数理统计”则是以概率论为基础,以数据为研究对象,研究如何有效地收集、整理、分析带有随机性的数据并建立模型,从而对随机现象的某些规律性进行推断或预测,为进一步的决策提供依据和建议.“概率论与数理统计”绪论4.与其它学科的联系及应用“概率论与数理统计”绪论“概率论与数理统计”以“微积分”、“线性代数”为基础;在许多领域有广泛的应用:工程技术 科学研究融投资经济管理 生产管理 等等是许多重要的新兴学科的基础:信息论

控制论可靠性理论基础:概率论与数理统计人工智能

信息编码理论

数据挖掘“概率论与数理统计”绪论统计4.与其它学科的联系及应用“概率论与数理统计”的理论与方法向各个学科的渗透,是近代科技发展的特征之一.“概率论与数理统计”与众多学科相结合产生出了许多边缘学科.金融统计学工程统商业统计学管理统计学计量经济学医学统计学生物统计学概率计学4.与其它学科的联系及应用如今的大数据时代更为“概率论与数理统计”的应用和发展提供了广阔的空间.“概率论与数理统计”绪论5.本课程的主要内容概率论基础随机变量及其分布多维随机变量及其分布随机变量的数字特征大数定律和中心极限定理数理统计基础参数估计假设检验“概率论与数理统计”绪论6.课程学习的目的为相关专业后续课程打基础;提高基本素养，面对生活或工作中的随机现象问题,要具有随机的思想,能够从概率的角度客观地分析问题、解决问题;

要具备对“数据”的敏感性,

能够使用正确的方法来处理或分析数据,从大量繁杂的数据中快速获取有用的信息.“概率论与数理统计”绪论7.关于教学方法的说明教学中略去一些复杂的理论推导和繁琐的手工计算,重点放在对理论的理解和应用方法掌握上.本课程采用大家熟知的EXCEL软件,有关实验讲解已录制成微课视频,可供同学们观看学习.“概率论与数理统计”绪论微课堂2222下列现象哪些是随机现象?那些是必然现象?（1）投掷飞镖射中的位置;抽查10件产品发现次品数;水从高处往低处流;一物体做匀速直线运动,走过的路程和时间成正比;明天的股票指数.“概率论与数理统计”绪论思考题2021年5月教学设计:主讲老师:徐雅静

汪远征

徐雅静

徐姗

郑州轻工业大学艺术设计:制作单位:制作时间:“概率论与数理统计”绪论第2讲

样本空间及随机事件徐雅静主讲微课堂为了研究随机现象的统计规律性需要进行试验.这里讲到的试验是一个含义广泛的术语.例如:“科学试验”“调查”“观察”“测量”样本空间及随机事件前言微课堂为了研究随机现象的统计规律性需要进行试验.(1)可以在相同条件下重复进行;(2)每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;(3)进行一次试验之前不能确定哪一个结果会出现.什么是随机试验?满足以下三个特点的试验称为随机试验:样本空间及随机事件前言微课堂(1)可以在相同条件下重复进行;(2)每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;(3)进行一次试验之前不能确定哪一个结果会出现.随机试验:样本空间及随机事件前言例如:“抛硬币”“掷骰子”“摇奖”2.样本空间【定义1】随机试验的一切可能基本结果组成的集合称为样本空间,记为

={

},

其中

表示某基本结果,

又称为样本点.【例2】给出几个随机试验的样本空间:“抛一枚硬币观察哪一面朝上”1

={正面向上,反面向上}.“掷一颗骰子观察朝上一面的点数”2

=

{1,

2,

3,

4,

5,

6}.样本空间及随机事件2.样本空间【定义1】随机试验的一切可能基本结果组成的集合称为样本空间,记为

={

},

其中

表示某基本结果,

又称为样本点.【例2】下面给出几个随机试验的样本空间:“检测某品牌电视机的寿命”3

=

{t

|

t

0}.“记录110某天接到的报警次数”4

=

{0,

1,

2,

…}.样本空间及随机事件2.样本空间【定义1】随机试验的一切可能基本结果组成的集合称为样本空间,记为

={

},

其中

表示某基本结果,

又称为样本点.【例2】下面给出几个随机试验的样本空间:·

“在以原点为圆心的单位圆内任取一点”5

=

{(x,

y)

|

x2

+

y2

<

1}.样本空间及随机事件2.样本空间1={正面向上,反面向上}.2

=

{1,

2,

3,

4,

5,

6}.3=

{t

|

t

0}.4=

{0,

1,

2,

…}.5=

{(x,

y)

|

x2

+

y2

<1}.说明:(1)样本点可以是数、非数、有限个,无限个、连续的数集,不连续的数集、一维的,二维的等.样本空间及随机事件观察这些样本空间最简单的样本空间什么样？2.样本空间样本空间及随机事件说明:一个样本空间可概括许多内容大不相同的实际问题.

例如:={H,T}可以作为:抛掷硬币试验的样本空间;质量管理中产品合格与不合格检验的样本空间;疾病诊断中的阴性阳性检验的样本空间;等等.想一想,为什么要了解随机试验的样本空间呢？3.随机事件什么是随机事件？简单来说,随机事件是指随机试验中可能发生也可能不发生的事件.当我们考虑一个随机事件时往往会和随机试验的若干个基本结果联系起来.比如:“掷骰子出现偶数点”{2,4,6},“掷骰子出现点数大于4”{5,6}于是有定义:样本空间及随机事件3.随机事件【定义2】随机试验的若干个基本结果组成的集合(样本空间的子集)称为随机事件,简称事件.只含有一个基本结果的事件称为基本事件.·

随机事件常用大写英文字母A,B,C,…来表示.样本空间及随机事件3.随机事件【定义2】随机试验的若干个基本结果组成的集合(样本空间的子集)称为随机事件,简称事件.只含有一个基本结果的事件称为基本事件.事件A发生当且仅几点说明:·

(1)随机事件可以用样本空间的子集表示,当对应集合中某个样本点出现了;例如:随机事件A

=“掷一颗骰子出现偶数点”,可以表示为A

={2,4,6}.样本空间及随机事件3.随机事件【定义2】随机试验的若干个基本结果组成的集合(样本空间的子集)称为随机事件,简称事件.只含有一个基本结果的事件称为基本事件.几点说明:(2)基本事件是只含有一个样本点的集合;例如:事件A

=“掷一颗骰子出现5点”,可记为A

={5},它是一个基本事件.掷一颗骰子共有6个基本事件.样本空间及随机事件3.随机事件在每次试验中几点说明:(3)两个特殊的事件:样本空间 是自身的子集,包含所有的样本点,它总是

发生的,

称为必然事件.空集

也是样本空间

的子集,

不包含任何的样本点,

每次试验都不发生,

称为不可能事件.样本空间及随机事件微课堂样本空间及随机事件小结三个基本概念:随机

样本随机

试验

空间

事件想一想三个概念的联系微课堂写出下列随机试验的样本空间.1.同时掷三颗骰子,记录三颗骰子之和;2.生产产品直到得到10件正品,记录生产产品的总件数;样本空间及随机事件思考题2021年5月教学设计:主讲老师:徐雅静

汪远征

徐雅静

徐姗

郑州轻工业大学艺术设计:制作单位:制作时间:样本空间及随机事件第3讲

事件的关系徐雅静主讲微课堂研究随机现象时,我们常常要考虑一些事件之间的关系及运算.事件之间的关系类似于集合间的关系,主要有:包含相等互不相容(互斥)互逆(对立)事件的关系前言1.事件的关系或者B(1)包含若事件A的样本点都在B里面,则称A包含于B,包含A, 记为AB.也称A为B的子事件.B,意味着事件A发生必有事件B发生例如A

:A

=“掷骰子出现2点或4点”B

=“掷骰子出现偶数点”显然

A B,

或称A是B的子事件.事件的关系BAΩ用维恩图表示包含关系1.事件的关系或者B(1)包含若事件A的样本点都在B里面,则称A包含于B,包含A, 记为AB.也称A为B的子事件.A B,意味着事件A发生必有事件B发生再例如:A

=“上课有女生迟到”,B

=

“上课有人迟到”显然也有A B,

A是B的子事件.事件的关系1.事件的关系(2)相等若A

B且BA,称A与B相等,记为A

=B.事件的关系两个事件相等意味着这两个事件对应同一集合,实际上两事件为同一个事件.例如:A

=“掷两颗骰子点数之和为奇数”B

=“掷两颗骰子点数为一奇一偶”{(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(3,6),(所(所4,以1),A(=4B,.3),(4,A5和)B,对(5应,2了)相,(同5,的4集),合(5,6),(6,1),(6,3),(6,5)}1.事件的关系A与B互不相容(或互斥)意味着事件A和B不能同时发生.例如:A

=“掷骰子得到奇数点”,A

={B1,=“3,掷5}骰,子B

=得{到2,偶4,数,数6点}.”A与B互不相容.事件的关系(3)互不相容（互斥）如果事件A与事件B没有包含相同的样本点,则称A与B互不相容(或互斥).AB1.事件的关系事件的关系AΩ(4)对立（互逆）则称B与A对立(或互若B为在

中而不在A中的样本点组成的集合,逆),

称B为A的对立事件(逆事件).A的对立事件记作

A

.A

表示A不发生.显然:A与A互不相容.A

A.BA微课堂小结事件的关系事件的关系A发生必然导致B发生A、B中一个发生另一个也发生子事件A⊂B事件相等A=B互不相容（互斥）A、B不同时发生A和B中有且只有一个发生对立（互逆）B

A微课堂1.掷一枚骰子写出下列事件的关系:A

=“出现奇数点”,B

=“出现偶数点”,C

=“出现2或3点”,D

=“出现2或4点”E

=“出现的大于1小于等于3”.2.甲、乙、丙三人同时向一飞机射击,写出下列事件的关系:A

=“飞机被击中”,B

=“甲击中飞机”,C

=“甲乙两人同时击中飞机”,D

=“三人同时击中飞机”,E

=“飞机没有被击中”,F

=“至少有一人击中飞机”.事件的关系练习题2021年5月教学设计:主讲老师:徐雅静

汪远征

徐雅静

徐姗

郑州轻工业大学艺术设计:制作单位:制作时间:事件的关系第4讲

事件的运算徐雅静主讲微课堂复杂的事件往往由一些简单的事件构成.利用事件的关系和运算可以用简单事件表示复杂的事件,从而使复杂事件的研究变得方便.事件的运算包括:和运算、积运算、差运算事件的运算前言1.事件的运算(1)事件A与B的和由事件A和B中所有的样本点构成的事件,称为A与B的和事件,记为A∪B.和事件A∪B表示A和B至少有一个发生.例如:A=“男生有人迟到”B=“女生有人迟到”C=“有人迟到”,显然C

=A∪B.事件的运算AA

BB1.事件的运算为有限和;为无穷可列和.事件的运算(1)事件A与B的和由事件A和B中所有的样本点构成的事件,称为A和B的和事件,记为A∪B.和事件A∪B表示A和B至少有一个发生.推广:n·称Ai1

ii·称A1

i1.事件的运算(2)事件A与B的积由事件A和B中相同的样本点构成的事件,称为A与B的积事件,记为A∩B或AB.积事件AB表示事件A与B同时发生.事件的运算ABAB1.事件的运算(2)事件A与B的积由事件A和B中相同的样本点构成的事件,称为A和B的积事件,记为A∩B或AB.积事件AB表示事件A与B同时发生.例如:某种产品的合格与否是由该产品的长度与直径所决定,设A＝“长度合格”,“B

＝“直径合格”,C

=“产品合格”.显然C

=A∩B

=AB.事件的运算1.事件的运算事件的运算(2)事件A与B的积由事件A和B中相同的样本点构成的事件,称为A和B的积事件,记为A∩B或AB.积事件AB表示事件A与B同时发生.推广:n·

称A

为有限积;i

1

i称A

为无穷可列积.i

1

i事件的运算1.事件的运算(2)事件A与B的积如何用事件的和运算或积运算表示事件A

和B

互不相容与对立的关系？ABΩA、B

对立(互逆)A、B互不相容(互斥)ΩB

AAAB=AB=

且A∪B=Ω1.事件的运算事件的运算B(3)事件A与B的差由属于事件A而不属于事件B的样本点的全体组成的集合称为事件A与B的差事件,记为A

–B.A

–B表示A发生而B不发生.易见A

–

B

=A

ABAB

.AA-BABABΩ1.事件的运算事件的运算(3)事件A与B的差由属于事件A而不属于事件B的样本点的全体组成的集合称为事件A与B的差事件,记为A

–B.A

–B表示A发生而B不发生.例如:掷一枚骰子,A=“出现奇数点”,B=“出现数点小于5”,C=“出现5点”,由于A

={1,3,5},B

={1,2,3,4},C

={5}.所以C

=A

–BA

-

ABAB

.2.事件运算满足的定律事件的运算事件的运算性质和集合的运算性质相同.设A,B,C为事件,则有结合律:(A交换律:

A

B

B

A,AB

BA.B)

C

A(B

C

),(

AB)C

A(BC

).2.事件运算满足的定律事件的运算性质和集合的运算性质相同.设A,B,C为事件,则有分配律:对偶律:事件的运算(

A

B)C

(

AC

) (BC

),(

AB)

C

(

A

C

)(B

C

),A

B

A

B

,ABA

B.左边到右边,长线变短线,和变积,积变和.3.有关例题【例1】设A,B,C表示三个随机事件,试将下列事件用A,B,C表示出来.A

发生,且B与C至少有一个发生;A与B发生,而C不发生;A,B,C

中恰有一个发生;A,B,C

中至少有两个发生;A,B,C

中至多有两个发生.事件的运算事件的运算3.有关例题【例1】设A,B,C表示三个随机事件,试将下列事件用A,B,C表示出来.A

发生,且B与C至少有一个发生;A与B发生,而C不发生;A,B,C

中恰有一个发生;C

)解:(1)A(B(2)

ABC；(2)

ABC

ABC

ABC3.有关例题【例1】