结构动力学之结构的极限荷载课件

结构的塑性分析与极限荷载

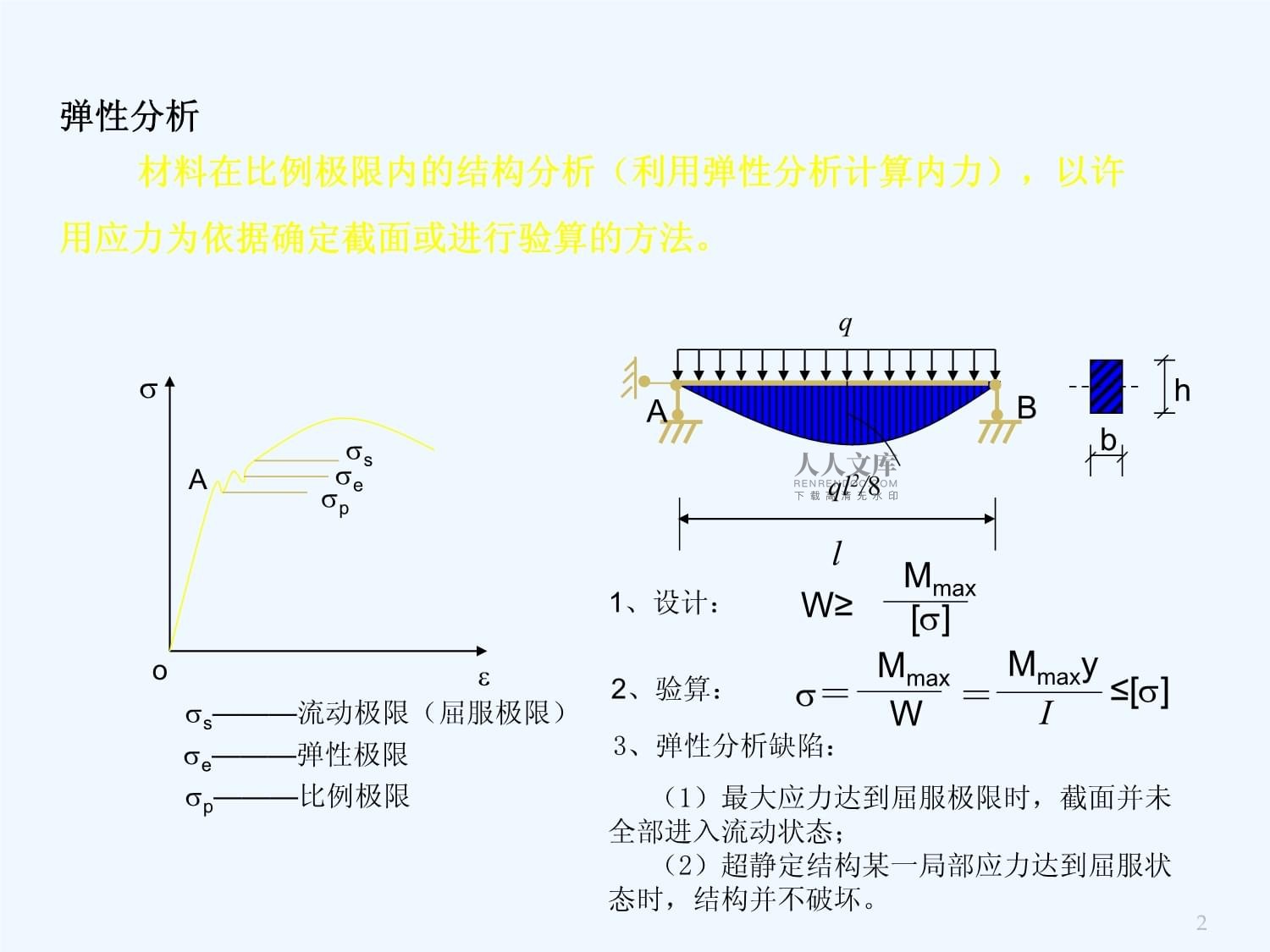
前面的计算都是在结构的线弹性范围内，荷载卸除后没有残余变形。弹性设计，在结构的局部甚至一个截面超过弹性极限，就认为结构发生破坏，弹性计算是精确的。对于非弹性材料，特别是超静定结构，最大应力超过弹性极限，甚至局部进入塑性，结构仍然能够继续加载，因此，弹性设计是不经济的。结构的塑性分析与极限荷载

前面的计算都是在结构的线弹性范围内11、设计：W≥[]Mmax2、验算：＝WMmax＝IMmaxy≤[]s———流动极限（屈服极限）e———弹性极限p———比例极限sepoA3、弹性分析缺陷：（1）最大应力达到屈服极限时，截面并未全部进入流动状态；（2）超静定结构某一局部应力达到屈服状态时，结构并不破坏。ql2/8hbqlAB弹性分析材料在比例极限内的结构分析（利用弹性分析计算内力），以许用应力为依据确定截面或进行验算的方法。1、设计：W≥[]Mmax2、验算：＝WMmax＝IMm2结构的塑性分析结构的塑性分析：基于考虑材料塑性性质的结构分析。其任务是研究结构处于塑性状态下的性能，确定结构破坏时所能承受的荷载---极限荷载。极限荷载：结构的变形随荷载的增加而增大。当荷载达到某一临界值时，不再增加荷载变形也会继续增大，这时结构丧失了进一步的承载能力，这种状态称为结构的极限状态，此时的荷载是结构所能承受的荷载极限，称为极限荷载，记作Pu。弹性设计时的强度条件：塑性设计时的强度条件：结构的塑性分析结构的塑性分析：极限荷载：弹性设计时的强度条件3结构的塑性分析与极限荷载

计算假定：材料为理想弹塑性材料。2.极限弯矩、塑性铰和极限状态变形的平面假设结构的塑性分析与极限荷载

计算假定：材料为理想弹塑性材料。24结构的塑性分析与极限荷载

1.弹性阶段---应力应变关系---应变与曲率关系---应力与曲率关系---弯矩与曲率关系---弹性极限弯矩(屈服弯矩)线性关系结构的塑性分析与极限荷载

1.弹性阶段---应力应变关系--5结构的塑性分析与极限荷载

2.弹塑性阶段中性轴附近处于弹性状态.处于弹性的部分称为弹性核.---弯矩与曲率关系非线性关系或3.塑性流动阶段---塑性极限弯矩(简称为极限弯矩)结构的塑性分析与极限荷载

2.弹塑性阶段中性轴附近处于弹性状6屈服弯矩与极限弯矩1、屈服弯矩（Ms):

截面最外侧纤维的应力达到流动极限时对应的弯矩。2、极限弯矩（Mu):

整个截面达到塑性流动状态时，对应的弯矩。s屈服弯矩与极限弯矩1、屈服弯矩（Ms):截面最外侧纤维的7极限弯矩3、截面形状系数：极限弯矩与屈服弯矩之比4、截面达到极限弯矩时的特点极限状态时，无论截面形状如何，中性轴两侧的拉压面积相等。依据这一特点可确定极限弯矩。hbMu极限弯矩3、截面形状系数：极限弯矩与屈服弯矩之比4、截面达到8极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有关。设截面上受压和受拉的面积分别为和，当截面上无轴力作用时中性轴亦为等分截面轴。由此可得极限弯矩的计算方法式中例：已知材料的屈服极限，求图示截面的极限弯矩。100mm20mm解:A1形心距下端0.045m,A2形心距上端0.01167m,A1与A2的形心距为0.0633m.极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有9形心轴，两侧面积矩相同，惯性轴等面积轴，两侧面积相同随内力的增大，中性轴在外侧应力达到屈服后，开始离开形心轴，逐步向等面积轴靠近，截面的极限弯矩由等面积轴确定。对称截面二轴重合极限弯矩形心轴，两侧面积矩相同，惯性轴等面积轴，两侧面积相同随内力的10圆形截面极限弯矩圆形截面极限弯矩11塑性铰若截面弯矩达到极限弯矩,这时的曲率记作。意味着该截面两侧可以发生相对转角，形如一个铰链。称为塑性铰。塑性铰与铰的差别：1.塑性铰可承受极限弯矩;2.塑性铰是单向的;3.卸载时消失;4.随荷载分布而出现于不同截面。塑性铰若截面弯矩达到极限弯矩,这时的曲率记作。意味着该12破坏机构结构由于出现塑性铰而形成的机构称为破坏机构。破坏机构可以是整体性的，也可能是局部的。破坏机构结构由于出现塑性铰而形成的机构称为破坏机构。破坏机构13由于足够多的塑性铰的出现，使原结构成为机构（几何可变体系），失去继续承载的能力，该几何可变体系称为“机构”。1、不同结构在荷载作用下，成为机构，所需塑性铰的数目不同。2、不同结构，只要材料、截面积、截面形状相同，塑性弯矩一定相同。MuMuMuMu3、材料、截面积、截面形状相同的不同结构，qu不一定相同。Mu1Mu2Mu2破坏机构由于足够多的塑性铰的出现，使原结构成为机构（几14如何确定单跨梁的极限荷载（1）弹性阶段（2）弹性阶段末MuMuMu（4）极限状态（3）梁两端出现塑性铰MuMu机理如何确定单跨梁的极限荷载（1）弹性阶段（2）弹性阶段末MuM15确定单跨梁极限荷载的机动法MuMuMu确定单跨梁极限荷载的机动法MuMuMu16确定复杂结构极限荷载面临的问题BACDB机构（一）CDAB机构（二）CDAB

情况（1）ACDB情况（2）ACD确定复杂结构极限荷载面临的问题BACDB机构（一）CDAB机17试确定图示单跨梁的极限荷载BB机构（一）B机构（二）B机构（一）M图情况B机构（二）M图情况确定单跨梁极限荷载的机动法试确定图示单跨梁的极限荷载BB机构（一）B机构（二）B机构（182、小变形假设（几何线形），变形后仍用变形前的几何尺寸。3、略去弹性变形（弹塑性材料，刚塑性变形。）确定极限荷载的几个定理一、几点假设1、比例加载4、不计剪力、轴力对极限荷载的影响5、正负极限弯矩值相等MuMuMu2、小变形假设（几何线形），变形后仍用变形前的几何尺寸。3、192、屈服条件当荷载达到极限值时，结构上各截面的弯矩都不能超过其极限值。3、平衡条件当荷载达到极限值时，作用在结构整体上或任意局部上的所有的力都必须保持平衡。结构极限状态时应满足的三个条件1、机构条件

当荷载达到极限值时，结构上必须有足够多的塑性铰，而使结构变成机构。2、屈服条件3、平衡条件结构极限状态时应满足的三个条件1、机202、可接受荷载屈服条件（p-)

根据静力可能而又安全的内力分布求得的荷载。它满平衡条件和屈服条件。3、极限荷载（pu)

同时满足机构条件、平衡条件和屈服条件的荷载。它既是可破坏荷载，又是可接受荷载。三个定义1、可破坏荷载（p+)

对任意单向破坏机构，根据平衡条件求得的荷载。它满足机构条件和平衡条件。2、可接受荷载屈服条件（p-)3、极限荷载（pu)三个定义1212、下限定理（亦称“静力定理”、或“极大定理”)

或：“可接受荷载的最大值是极限荷载的下限”。或：“极限荷载是可接受荷载的最大值”3、单值定理（亦称“唯一定理”)“既是可破坏荷载，又是可接受荷载，则此荷载是极限荷载”。或：“极限荷载是唯一的”确定极限荷载三个定理1、上限定理（亦称“机动定理”、或“极小定理”)

对于比例加载作用下的给定结构，按任意可能的破坏机构，由平衡条件求得的荷载将大于或等于极限荷载。或：“可破坏荷载的最小值是极限荷载的上限”。或：“极限荷载是可破坏荷载的最小值”…………一系列可破坏荷载的最小值一系列可接受荷载的最大值极限荷载2、下限定理（亦称“静力定理”、或“极大定理”)3、单值定理22超静定梁的极限荷载一、确定极限荷载的三种方法

1、机动法

2、静力法

3、试算法二、机动法1、依据：机动法是以上限定理为依据的。2、步骤：先假设出所有的破坏机构，而后利用虚位移原理计算出各机构相应的极限荷载。依据上限定理，这些可破坏荷载中的最小者即为极限荷载。三、试算法1、依据：试算法是以单值定理为依据的。2、步骤：先试算出相应于某一破坏机构的可破坏荷载，而后验算该荷载是否满足屈服条件，若满足，该荷载即为极限荷载。超静定梁的极限荷载一、确定极限荷载的三种方法二、机动法23例题1试用机动法求图示结构的极限荷载。MuMu机构（1）MuMu机构（2）例题1试用机动法求图示结构的极限荷载。MuMu机构（1）24MuMu机构（3）结论：机构（3）、（4）不会出现，各跨可单独考虑。MuMu机构（4）例题1试用机动法求图示结构的极限荷载。MuMu机构（3）结论：机构（3）、（4）不会出现，各跨可单25例题2试用试算法求图示结构的极限荷载。MuMu机构（1）MuMuM图例题2试用试算法求图示结构的极限荷载。MuMu机构（1）26例题2试用试算法求图示结构的极限荷载。MuMuM图MuMu机构（2）例题2试用试算法求图示结构的极限荷载。MuMuM图Mu27结构的塑性分析与极限荷载

前面的计算都是在结构的线弹性范围内，荷载卸除后没有残余变形。弹性设计，在结构的局部甚至一个截面超过弹性极限，就认为结构发生破坏，弹性计算是精确的。对于非弹性材料，特别是超静定结构，最大应力超过弹性极限，甚至局部进入塑性，结构仍然能够继续加载，因此，弹性设计是不经济的。结构的塑性分析与极限荷载

前面的计算都是在结构的线弹性范围内281、设计：W≥[]Mmax2、验算：＝WMmax＝IMmaxy≤[]s———流动极限（屈服极限）e———弹性极限p———比例极限sepoA3、弹性分析缺陷：（1）最大应力达到屈服极限时，截面并未全部进入流动状态；（2）超静定结构某一局部应力达到屈服状态时，结构并不破坏。ql2/8hbqlAB弹性分析材料在比例极限内的结构分析（利用弹性分析计算内力），以许用应力为依据确定截面或进行验算的方法。1、设计：W≥[]Mmax2、验算：＝WMmax＝IMm29结构的塑性分析结构的塑性分析：基于考虑材料塑性性质的结构分析。其任务是研究结构处于塑性状态下的性能，确定结构破坏时所能承受的荷载---极限荷载。极限荷载：结构的变形随荷载的增加而增大。当荷载达到某一临界值时，不再增加荷载变形也会继续增大，这时结构丧失了进一步的承载能力，这种状态称为结构的极限状态，此时的荷载是结构所能承受的荷载极限，称为极限荷载，记作Pu。弹性设计时的强度条件：塑性设计时的强度条件：结构的塑性分析结构的塑性分析：极限荷载：弹性设计时的强度条件30结构的塑性分析与极限荷载

计算假定：材料为理想弹塑性材料。2.极限弯矩、塑性铰和极限状态变形的平面假设结构的塑性分析与极限荷载

计算假定：材料为理想弹塑性材料。231结构的塑性分析与极限荷载

1.弹性阶段---应力应变关系---应变与曲率关系---应力与曲率关系---弯矩与曲率关系---弹性极限弯矩(屈服弯矩)线性关系结构的塑性分析与极限荷载

1.弹性阶段---应力应变关系--32结构的塑性分析与极限荷载

2.弹塑性阶段中性轴附近处于弹性状态.处于弹性的部分称为弹性核.---弯矩与曲率关系非线性关系或3.塑性流动阶段---塑性极限弯矩(简称为极限弯矩)结构的塑性分析与极限荷载

2.弹塑性阶段中性轴附近处于弹性状33屈服弯矩与极限弯矩1、屈服弯矩（Ms):

截面最外侧纤维的应力达到流动极限时对应的弯矩。2、极限弯矩（Mu):

整个截面达到塑性流动状态时，对应的弯矩。s屈服弯矩与极限弯矩1、屈服弯矩（Ms):截面最外侧纤维的34极限弯矩3、截面形状系数：极限弯矩与屈服弯矩之比4、截面达到极限弯矩时的特点极限状态时，无论截面形状如何，中性轴两侧的拉压面积相等。依据这一特点可确定极限弯矩。hbMu极限弯矩3、截面形状系数：极限弯矩与屈服弯矩之比4、截面达到35极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有关。设截面上受压和受拉的面积分别为和，当截面上无轴力作用时中性轴亦为等分截面轴。由此可得极限弯矩的计算方法式中例：已知材料的屈服极限，求图示截面的极限弯矩。100mm20mm解:A1形心距下端0.045m,A2形心距上端0.01167m,A1与A2的形心距为0.0633m.极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有36形心轴，两侧面积矩相同，惯性轴等面积轴，两侧面积相同随内力的增大，中性轴在外侧应力达到屈服后，开始离开形心轴，逐步向等面积轴靠近，截面的极限弯矩由等面积轴确定。对称截面二轴重合极限弯矩形心轴，两侧面积矩相同，惯性轴等面积轴，两侧面积相同随内力的37圆形截面极限弯矩圆形截面极限弯矩38塑性铰若截面弯矩达到极限弯矩,这时的曲率记作。意味着该截面两侧可以发生相对转角，形如一个铰链。称为塑性铰。塑性铰与铰的差别：1.塑性铰可承受极限弯矩;2.塑性铰是单向的;3.卸载时消失;4.随荷载分布而出现于不同截面。塑性铰若截面弯矩达到极限弯矩,这时的曲率记作。意味着该39破坏机构结构由于出现塑性铰而形成的机构称为破坏机构。破坏机构可以是整体性的，也可能是局部的。破坏机构结构由于出现塑性铰而形成的机构称为破坏机构。破坏机构40由于足够多的塑性铰的出现，使原结构成为机构（几何可变体系），失去继续承载的能力，该几何可变体系称为“机构”。1、不同结构在荷载作用下，成为机构，所需塑性铰的数目不同。2、不同结构，只要材料、截面积、截面形状相同，塑性弯矩一定相同。MuMuMuMu3、材料、截面积、截面形状相同的不同结构，qu不一定相同。Mu1Mu2Mu2破坏机构由于足够多的塑性铰的出现，使原结构成为机构（几41如何确定单跨梁的极限荷载（1）弹性阶段（2）弹性阶段末MuMuMu（4）极限状态（3）梁两端出现塑性铰MuMu机理如何确定单跨梁的极限荷载（1）弹性阶段（2）弹性阶段末MuM42确定单跨梁极限荷载的机动法MuMuMu确定单跨梁极限荷载的机动法MuMuMu43确定复杂结构极限荷载面临的问题BACDB机构（一）CDAB机构（二）CDAB

情况（1）ACDB情况（2）ACD确定复杂结构极限荷载面临的问题BACDB机构（一）CDAB机44试确定图示单跨梁的极限荷载BB机构（一）B机构（二）B机构（一）M图情况B机构（二）M图情况确定单跨梁极限荷载的机动法试确定图示单跨梁的极限荷载BB机构（一）B机构（二）B机构（452、小变形假设（几何线形），变形后仍用变形前的几何尺寸。3、略去弹性变形（弹塑性材料，刚塑性变形。）确定极限荷载的几个定理一、几点假设1、比例加载4、不计剪力、轴力对极限荷载的影响5、正负极限弯矩值相等MuMuMu2、小变形假设（几何线形），变形后仍用变形前的几何尺寸。3、462、屈服条件当荷载达到极限值时，结构上各截面的弯矩都不能超过其极限值。3、平衡条件当荷载达到极限值时，作用在结构整体上或任意局部上的所有的力都必须保持平衡。结构极限状态时应满足的三个条件1、机构条件

当荷载达到极限值时，结构上必须有足够多的塑性铰，而使结构变成机构。2、屈服条件3、平衡条件结构极限状态时应满足的三个条件1、机472、可接受荷载屈服条件（p-)

根据静力可能而又安全的内力分布求得的荷载。它满平衡条件和屈服条件。3、极限荷载（pu)

同时满足机构条件、平衡条件和屈服条件的荷载。它既是可破坏荷载，又是可接受荷载。三个定义1、可破坏荷载（p+)

对任意单向破坏机构，根据平衡条件求得的荷载。它满足机构条件和平衡条件。2、可接受荷载屈服条件（p-)3、极限荷载（pu)三个定义1482、下限定理（亦称“静力定理”、或“极大定理”)

或：“可接受荷载的最大值是极限荷载的下限”。或：“极限荷载是可接受荷载的最大值”3、单值定理（亦称“唯一定理”)“既是可破坏荷载，又是可接受荷载，则此荷载是极限荷载”。或：“极限荷载是唯一的”确定极限荷载三个定理1、上限定理（亦称“机动定理”、或“极小定理”)