线段和差的最值问题教案课件

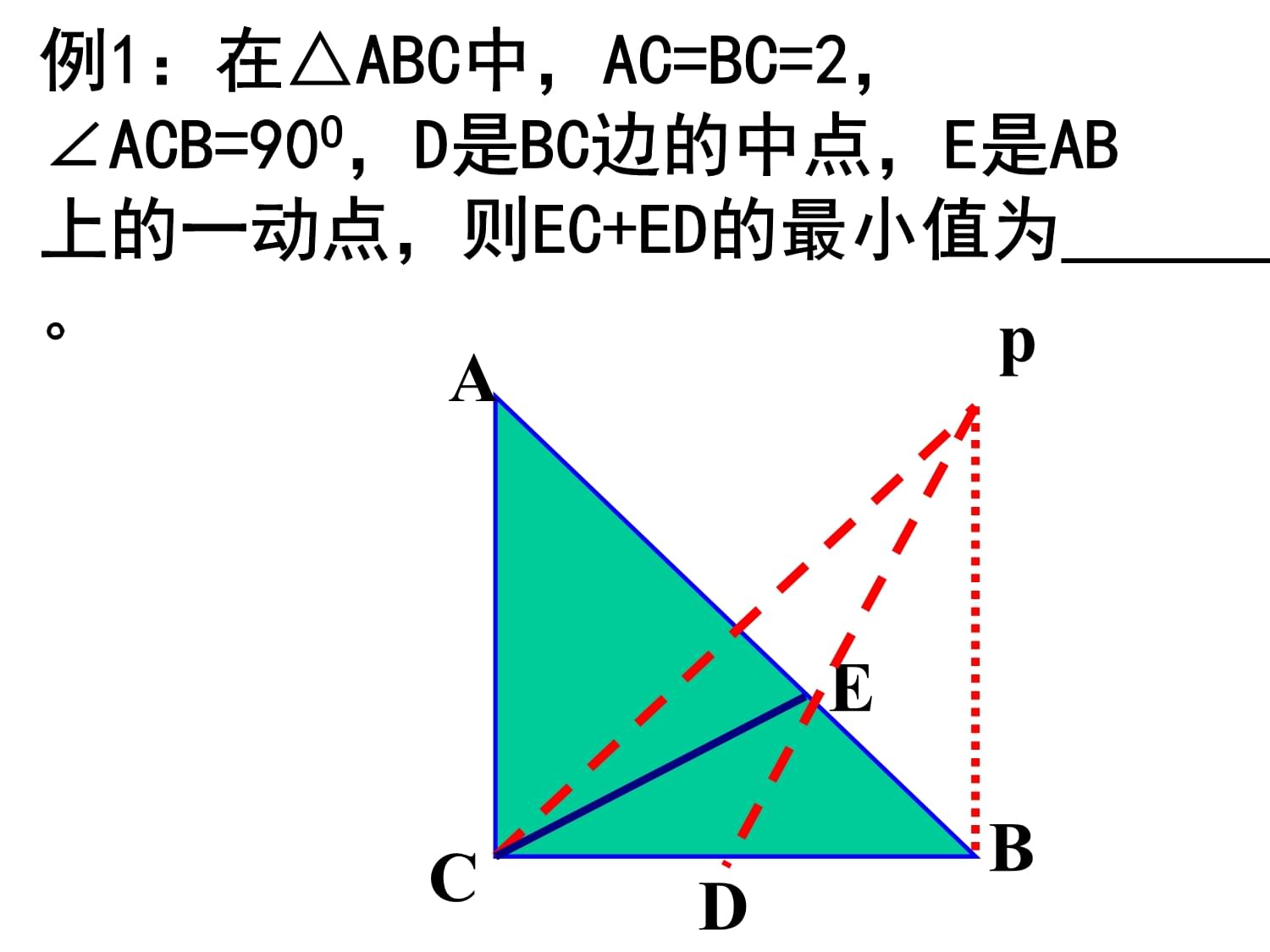
线段和差的最值问题解题策略单人棋2014年10月线段和差的最值问题解题策略两条线段和的最小值两点之间，线段最短线段和差的最值问题解题策略两条线段差的最大值三角形两边之差小于第三边当P运动到E时，PA＋PB最小当Q运动到F时，QD－QC最大两条线段和的最小值线段和差的最值问题解题策略两条线段差的最大线段和差的最值问题解题策略当P运动到E时，PA＋PB最小当Q运动到F时，QD－QC最大第一步，寻找、构造几何模型第二步，计算线段和差的最值问题解题策略当P运动到E时，PA＋PB最小当Q一、求两条线段之和的最小值一、求两条线段之和的最小值例1：在△ABC中，AC=BC=2，∠ACB=90O，D是BC边的中点，E是AB上的一动点，则EC+ED的最小值为

。ACBDEp例1：在△ABC中，AC=BC=2，∠ACB=90O，D是B例2：△ABC中，AC=3，BC=4，AB=5，试在AB上找一点P，在BC上取一点M，使CP+PM的值最小，并求出这个最小值。ABCPMC/例2：△ABC中，AC=3，BC=4，AB=5，试在AB上找例1、例2中的最小值问题，所涉及到的路径，虽然都是由两条线段连接而成，但是路径中的动点与定点的个数不同，例1中的路径为“定点→动点→定点”，是两个定点一个动点，而例2中的路径是“定点→动点→动点”，是一个定点两个动点，所以两个题的解法有较大差异，例1是根据两点之间线段最短求动点的位置，例2是根据垂线段最短找两个动点的位置。规律总结例1、例2中的最小值问题，所涉及到的路径，虽然都是由两条线段二、求三角形周长的最小值二、求三角形周长的最小值例3：已知二次函数图像的顶点坐标为C(3，-2)，且在x轴上截得的线段AB的长为4，在y轴上有一点P，使△APC的周长最小，求P点坐标。ACBA/OP例3：已知二次函数图像的顶点坐标为C(3，-2)，且在x轴上例4：抛物线y=ax2+bx+c经过点A(-4，3)，B(2，0)，当x=3和x=-3时，这条抛物线上对应点的纵坐标相等，经过点C(0，-2）的直线a与x轴平行。（1）求直线AB和抛物线，（2）设直线AB上点D的横坐标为-1，P(m，n)是抛物线上的一动点，当△POD的周长最小时，求P点坐标。2010•南通）已知抛物线y=ax2+bx+c经过A（-4，3）、B（2，0）两点，当x=3和x=-3时，这条抛物线上对应点的纵坐标相等．经过点C（0，-2）的直线l与x轴平行，O为坐标原点．

（1）求直线AB和这条抛物线的解析式；

（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；

（3）设直线AB上的点D的横坐标为-1，P（m，n）是抛物线y=ax2+bx+c上的动点，当△PDO的周长最小时，求四边形CODP的面积．考点：二次函数综合题．专题：压轴题．分析：（1）用待定系数法即可求出直线AB的解析式；根据“当x=3和x=-3时，这条抛物线上对应点的纵坐标相等”可知：抛物线的对称轴为y轴，然后用待定系数法即可求出抛物线的解析式；

（2）根据A点坐标可求出半径OA的长，然后判断A到直线l的距离与半径OA的大小关系即可；

（3）根据直线AB的解析式可求出D点的坐标，即可得到OD的长，由于OD的长为定值，若△POD的周长最小，那么PD+OP的长最小，可过P作y轴的平行线，交直线l于M；首先证PO=PM，此时PD+OP=PD+PM，而PD+PM≥DM，因此PD+PM最小时，应有PD+PM=DM，即D、P、M三点共线，由此可求得P点的坐标；此时四边形CODP是梯形，根据C、O、D、P四点坐标即可求得上下底DP、OC的长，而梯形的高为D点横坐标的绝对值由此可求出四边形CODP的面积．解答：解：（1）设直线AB的解析式为y=kx+b，则有：

−4k+b＝32k+b＝0，

解得k＝−12b＝1；

∴直线AB的解析式为y=-12x+1；

由题意知：抛物线的对称轴为y轴，则抛物线经过（-4，3），（2，0），（-2，0）三点；

设抛物线的解析式为：y=a（x-2）（x+2），

则有：3=a（-4-2）（-4+2），a=14；

∴抛物线的解析式为：y=14x2-1；

（2）易知：A（-4，3），则OA=42+32=5；

而A到直线l的距离为：3-（-2）=5；

所以⊙A的半径等于圆心A到直线l的距离，

即直线l与⊙A相切；

（3）过D点作DM∥y轴交直线于点M交抛物线于点P，

则P（m，n），M（m，-2）；

∴PO2=m2+n2，PM2=（n+2）2；

∵n=14m2-1，即m2=4n+4；

∴PO2=n2+4n+4=（n+2）2，

即PO2=PM2，PO=PM；

易知D（-1，32），则OD的长为定值；

若△PDO的周长最小，则PO+PD的值最小；

∵PO+PD=PD+PM≥DM，

∴PD+PO的最小值为DM，

即当D、P、M三点共线时PD+PM=PO+PD=DM；

此时点P的横坐标为-1，代入抛物线的解析式可得y=14-1=-34，

即P（-1，-34）；

∴S四边形CPDO=12（CO+PD）×|xD|=12×（2+32+34）×1=178．点评：此题主要考查了二次函数解析式的确定、直线与圆的位置关系、图形面积的求法等知识，还涉及到解析几何中抛物线的相关知识，能力要求极高，难度很大．例4：抛物线y=ax2+bx+c经过点A(-4，3)，B(2ABOCDPABOCDPABOCDPABOCDP规律总结例3，例4中最小值问题，所涉及到的路径虽然都是有两条动线段连接而成，且路径都是“定点→动点→定点”，但是动点运动的路线不同，例3是直线，例4是曲线，因此它们的解法有很大不同，例3是根据两点之间线段最短找到动点的位置，例4是根据垂线段最短找到所求的两个动点的位置。规律总结例3，例4中最小值问题，所涉及到的路径虽然都是有两条三、求四边形周长最小值问题三、求四边形周长最小值问题例5:在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小？如果存在,求出周长的最小值;如果不存在,请说明理由.例5:在x轴、y轴上是否分别存在点M、N,使得四边形MNFE要求四边形MNFE的周长最小？把三条线段转移到同一条直线上就好了！第一步

寻找、构造几何模型EFE/F/MN要求四边形MNFE的周长最小？把三条线段转移到同一条直线上就第二步

计算——勾股定理第二步计算——勾股定理小结线段和差的最值问题解题策略经典模型：台球两次碰壁问题经验储存：没有经验，难有思路小结线段和差的最值问题解题策略经典模型：台球两次碰壁问题经验例6：在平面直角坐标系中，Rt△AOB的顶点坐标分别是A(-2，0)，O(0,0)，B(0，4），把△AOB绕O点按顺时针旋转90度，得到△COD，（1）求C、D的坐标，（2）求经过A、B、D三点的抛物线。（3）在（2）中的抛物线的对称轴上取两点E、F（E在F点的上方），且EF=1，当四边形ACEF的周长最小时，求E、F的坐标。例6：在平面直角坐标系中，Rt△AOB的顶点坐标分别是A(-ABCEFDD/OABCEFDD/O规律总结例5、例6中的最小值问题所涉及到的路径，虽然都是由三条动线段连接而成，且路径都是“定点→动点→动点→定点”，但是例5中的量动点间的线段长度不确定，而例6的两动点间的线段长度为定值，正是由于这点的不同，使得它们的解题方法有很大差异，例5是根据两点之间线段最短找到动点的位置，例6是通过构造平行四边形先找到所求的其中一个动点的位置，另一个位置也随之确定。规律总结例5、例6中的最小值问题所涉及到的路径，虽然都是由三1、已知在对抛物线的对称轴上存在一点P，使得△PBC的周长最小，请求出点P的坐标.1、已知在对抛物线的对称轴上存在一点P，使得△PBC的周长最要求△PBC的周长最小？第一步

寻找、构造几何模型只要PB+PC最小就好了！经典模型：牛喝水！要求△PBC的周长最小？第一步寻找、构造几何模型只要PB线段和差的最值问题解题策略把PB+PC转化为PA+PC

！当P运动到H时，PA+PC最小第二步

计算——勾股定理线段和差的最值问题解题策略把PB+PC转化为PA+PC！当2、对于动点Q（1，n），求PQ+QB的最小值.2、对于动点Q（1，n），要求PQ+QB的最小值？线段和差的最值问题解题策略第一步

寻找、构造几何模型经典模型：牛喝水！要求PQ+QB的最小值？线段和差的最值问题解题策略第一步线段和差的最值问题解题策略把PQ+QB转化为PQ+QA

！当Q运动到E时，PQ+QA最小第二步

计算——勾股定理线段和差的最值问题解题策略把PQ+QB转化为PQ+QA！当线段和差的最值问题解题策略第二步

计算——勾股定理把PQ+QB转化为PQ+QA

！当Q运动到E时，PQ+QA最小线段和差的最值问题解题策略第二步计算——勾股定理把PQ+线段和差的最值问题解题策略小结E?F!线段和差的最值问题解题策略小结E?F!3.如图，∠AOB=45，角内有一动点P，PO=10，在AO，BO上有两动点Q，R，求△PQR周长的最小值。ABOPDERQ3.如图，∠AOB=45，角内有一动点P，PO=10，在A4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD（不含B点）上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证：△AMB≌△ENB；⑵①当M点在何处时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；EA

DBCNM4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为爱是什么？

一个精灵坐在碧绿的枝叶间沉思。

风儿若有若无。

一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。

精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？”

“爱。”

“为什么？”

“它驱赶我的饥饿。”

鸟儿啄完稻谷，轻轻梳理着光润的羽毛。

“现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。

鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。”

精灵摘下一片树叶，里面盛了一汪泉水。

鸟儿喝完泉水，准备振翅飞去。

“请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。

“你要去做什么更重要的事吗？我这里又稻谷也有泉水。”

“我要去那片开着风信子的山谷，去看那朵风信子。”

“为什么？它能驱赶你的饥饿？”

“不能。”

“它能滋润你的干渴？”

“不能。”爱是什么？

一个精灵坐在碧绿的枝叶间沉思。

风儿若有若无。

一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。

精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？”

“爱。”

“为什么？”

“它驱赶我的饥饿。”

鸟儿啄完稻谷，轻轻梳理着光润的羽毛。

“现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。

鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。”

精灵摘下一片树叶，里面盛了一汪泉水。

鸟儿喝完泉水，准备振翅飞去。

“请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。

“你要去做什么更重要的事吗？我这里又稻谷也有泉水。”

“我要去那片开着风信子的山谷，去看那朵风信子。”

“为什么？它能驱赶你的饥饿？”

“不能。”

“它能滋润你的干渴？”

“不能。”爱是什么？

一个精灵坐在碧绿的枝叶间沉思。

风儿若有若无。

其实，世上最温暖的语言，“不是我爱你，而是在一起。”

所以懂得才是最美的相遇！只有彼此以诚相待，彼此尊重，相互包容，相互懂得，才能走的更远。相遇是缘，相守是爱。缘是多么的妙不可言，而懂得又是多么的难能可贵。否则就会错过一时，错过一世！择一人深爱，陪一人到老。一路相扶相持，一路心手相牵，一路笑对风雨。在平凡的世界，不求爱的轰轰烈烈；不求誓言多么美丽；唯愿简单的相处，真心地付出，平淡地相守，才不负最美的人生；不负善良的自己。人海茫茫，不求人人都能刻骨铭心，但求对人对己问心无愧，无怨无悔足矣。大千世界，与万千人中遇见，只是相识的开始，只有彼此真心付出，以心交心，以情换情，相知相惜，才能相伴美好的一生，一路同行。然而，生活不仅是诗和远方，更要面对现实。如果曾经的拥有，不能天长地久，那么就要学会华丽地转身，学会忘记。忘记该忘记的人，忘记该忘记的事儿，忘记苦乐年华的悲喜交集。人有悲欢离合，月有阴晴圆缺。对于离开的人，不必折磨自己脆弱的生命，虚度了美好的朝夕；不必让心灵痛苦不堪，弄丢了快乐的自己。擦汗眼泪，告诉自己，日子还得继续，谁都不是谁的唯一，相信最美的风景一直在路上。人生，就是一场修行。你路过我，我忘记你；你有情，他无意。谁都希望在正确的时间遇见对的人，然而事与愿违时，你越渴望的东西，也许越是无情无义地弃你而去。所以美好的愿望，就会像肥皂泡一样破灭，只能在错误的时间遇到错的人。岁月匆匆像一阵风，有多少故事留下感动。愿曾经的相遇，无论是锦上添花，还是追悔莫及；无论是青涩年华的懵懂赏识，还是成长岁月无法躲避的经历……愿曾经的过往，依然如花芬芳四溢，永远无悔岁月赐予的美好相遇。其实，人生之路的每一段相遇，都是一笔财富，尤其亲情、友情和爱情。在漫长的旅途上，他们都会丰富你的生命，使你的生命更充实，更真实；丰盈你的内心，使你的内心更慈悲，更善良。所以生活的美好，缘于一颗善良的心，愿我们都能善待自己和他人。一路走来，愿相亲相爱的人，相濡以沫，同甘共苦，百年好合。愿有情有意的人，不离不弃，相惜相守，共度人生的每一个朝夕……直到老得哪也去不了，依然是彼此手心里的宝，感恩一路有你！其实，世上最温暖的语言，“不是我爱你，而是在一起。”

线段和差的最值问题教案课件线段和差的最值问题解题策略单人棋2014年10月线段和差的最值问题解题策略两条线段和的最小值两点之间，线段最短线段和差的最值问题解题策略两条线段差的最大值三角形两边之差小于第三边当P运动到E时，PA＋PB最小当Q运动到F时，QD－QC最大两条线段和的最小值线段和差的最值问题解题策略两条线段差的最大线段和差的最值问题解题策略当P运动到E时，PA＋PB最小当Q运动到F时，QD－QC最大第一步，寻找、构造几何模型第二步，计算线段和差的最值问题解题策略当P运动到E时，PA＋PB最小当Q一、求两条线段之和的最小值一、求两条线段之和的最小值例1：在△ABC中，AC=BC=2，∠ACB=90O，D是BC边的中点，E是AB上的一动点，则EC+ED的最小值为

。ACBDEp例1：在△ABC中，AC=BC=2，∠ACB=90O，D是B例2：△ABC中，AC=3，BC=4，AB=5，试在AB上找一点P，在BC上取一点M，使CP+PM的值最小，并求出这个最小值。ABCPMC/例2：△ABC中，AC=3，BC=4，AB=5，试在AB上找例1、例2中的最小值问题，所涉及到的路径，虽然都是由两条线段连接而成，但是路径中的动点与定点的个数不同，例1中的路径为“定点→动点→定点”，是两个定点一个动点，而例2中的路径是“定点→动点→动点”，是一个定点两个动点，所以两个题的解法有较大差异，例1是根据两点之间线段最短求动点的位置，例2是根据垂线段最短找两个动点的位置。规律总结例1、例2中的最小值问题，所涉及到的路径，虽然都是由两条线段二、求三角形周长的最小值二、求三角形周长的最小值例3：已知二次函数图像的顶点坐标为C(3，-2)，且在x轴上截得的线段AB的长为4，在y轴上有一点P，使△APC的周长最小，求P点坐标。ACBA/OP例3：已知二次函数图像的顶点坐标为C(3，-2)，且在x轴上例4：抛物线y=ax2+bx+c经过点A(-4，3)，B(2，0)，当x=3和x=-3时，这条抛物线上对应点的纵坐标相等，经过点C(0，-2）的直线a与x轴平行。（1）求直线AB和抛物线，（2）设直线AB上点D的横坐标为-1，P(m，n)是抛物线上的一动点，当△POD的周长最小时，求P点坐标。2010•南通）已知抛物线y=ax2+bx+c经过A（-4，3）、B（2，0）两点，当x=3和x=-3时，这条抛物线上对应点的纵坐标相等．经过点C（0，-2）的直线l与x轴平行，O为坐标原点．

（1）求直线AB和这条抛物线的解析式；

（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；

（3）设直线AB上的点D的横坐标为-1，P（m，n）是抛物线y=ax2+bx+c上的动点，当△PDO的周长最小时，求四边形CODP的面积．考点：二次函数综合题．专题：压轴题．分析：（1）用待定系数法即可求出直线AB的解析式；根据“当x=3和x=-3时，这条抛物线上对应点的纵坐标相等”可知：抛物线的对称轴为y轴，然后用待定系数法即可求出抛物线的解析式；

（2）根据A点坐标可求出半径OA的长，然后判断A到直线l的距离与半径OA的大小关系即可；

（3）根据直线AB的解析式可求出D点的坐标，即可得到OD的长，由于OD的长为定值，若△POD的周长最小，那么PD+OP的长最小，可过P作y轴的平行线，交直线l于M；首先证PO=PM，此时PD+OP=PD+PM，而PD+PM≥DM，因此PD+PM最小时，应有PD+PM=DM，即D、P、M三点共线，由此可求得P点的坐标；此时四边形CODP是梯形，根据C、O、D、P四点坐标即可求得上下底DP、OC的长，而梯形的高为D点横坐标的绝对值由此可求出四边形CODP的面积．解答：解：（1）设直线AB的解析式为y=kx+b，则有：

−4k+b＝32k+b＝0，

解得k＝−12b＝1；

∴直线AB的解析式为y=-12x+1；

由题意知：抛物线的对称轴为y轴，则抛物线经过（-4，3），（2，0），（-2，0）三点；

设抛物线的解析式为：y=a（x-2）（x+2），

则有：3=a（-4-2）（-4+2），a=14；

∴抛物线的解析式为：y=14x2-1；

（2）易知：A（-4，3），则OA=42+32=5；

而A到直线l的距离为：3-（-2）=5；

所以⊙A的半径等于圆心A到直线l的距离，

即直线l与⊙A相切；

（3）过D点作DM∥y轴交直线于点M交抛物线于点P，

则P（m，n），M（m，-2）；

∴PO2=m2+n2，PM2=（n+2）2；

∵n=14m2-1，即m2=4n+4；

∴PO2=n2+4n+4=（n+2）2，

即PO2=PM2，PO=PM；

易知D（-1，32），则OD的长为定值；

若△PDO的周长最小，则PO+PD的值最小；

∵PO+PD=PD+PM≥DM，

∴PD+PO的最小值为DM，

即当D、P、M三点共线时PD+PM=PO+PD=DM；

此时点P的横坐标为-1，代入抛物线的解析式可得y=14-1=-34，

即P（-1，-34）；

∴S四边形CPDO=12（CO+PD）×|xD|=12×（2+32+34）×1=178．点评：此题主要考查了二次函数解析式的确定、直线与圆的位置关系、图形面积的求法等知识，还涉及到解析几何中抛物线的相关知识，能力要求极高，难度很大．例4：抛物线y=ax2+bx+c经过点A(-4，3)，B(2ABOCDPABOCDPABOCDPABOCDP规律总结例3，例4中最小值问题，所涉及到的路径虽然都是有两条动线段连接而成，且路径都是“定点→动点→定点”，但是动点运动的路线不同，例3是直线，例4是曲线，因此它们的解法有很大不同，例3是根据两点之间线段最短找到动点的位置，例4是根据垂线段最短找到所求的两个动点的位置。规律总结例3，例4中最小值问题，所涉及到的路径虽然都是有两条三、求四边形周长最小值问题三、求四边形周长最小值问题例5:在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小？如果存在,求出周长的最小值;如果不存在,请说明理由.例5:在x轴、y轴上是否分别存在点M、N,使得四边形MNFE要求四边形MNFE的周长最小？把三条线段转移到同一条直线上就好了！第一步

寻找、构造几何模型EFE/F/MN要求四边形MNFE的周长最小？把三条线段转移到同一条直线上就第二步

计算——勾股定理第二步计算——勾股定理小结线段和差的最值问题解题策略经典模型：台球两次碰壁问题经验储存：没有经验，难有思路小结线段和差的最值问题解题策略经典模型：台球两次碰壁问题经验例6：在平面直角坐标系中，Rt△AOB的顶点坐标分别是A(-2，0)，O(0,0)，B(0，4），把△AOB绕O点按顺时针旋转90度，得到△COD，（1）求C、D的坐标，（2）求经过A、B、D三点的抛物线。（3）在（2）中的抛物线的对称轴上取两点E、F（E在F点的上方），且EF=1，当四边形ACEF的周长最小时，求E、F的坐标。例6：在平面直角坐标系中，Rt△AOB的顶点坐标分别是A(-ABCEFDD/OABCEFDD/O规律总结例5、例6中的最小值问题所涉及到的路径，虽然都是由三条动线段连接而成，且路径都是“定点→动点→动点→定点”，但是例5中的量动点间的线段长度不确定，而例6的两动点间的线段长度为定值，正是由于这点的不同，使得它们的解题方法有很大差异，例5是根据两点之间线段最短找到动点的位置，例6是通过构造平行四边形先找到所求的其中一个动点的位置，另一个位置也随之确定。规律总结例5、例6中的最小值问题所涉及到的路径，虽然都是由三1、已知在对抛物线的对称轴上存在一点P，使得△PBC的周长最小，请求出点P的坐标.1、已知在对抛物线的对称轴上存在一点P，使得△PBC的周长最要求△PBC的周长最小？第一步

寻找、构造几何模型只要PB+PC最小就好了！经典模型：牛喝水！要求△PBC的周长最小？第一步寻找、构造几何模型只要PB线段和差的最值问题解题策略把PB+PC转化为PA+PC

！当P运动到H时，PA+PC最小第二步

计算——勾股定理线段和差的最值问题解题策略把PB+PC转化为PA+PC！当2、对于动点Q（1，n），求PQ+QB的最小值.2、对于动点Q（1，n），要求PQ+QB的最小值？线段和差的最值问题解题策略第一步

寻找、构造几何模型经典模型：牛喝水！要求PQ+QB的最小值？线段和差的最值问题解题策略第一步线段和差的最值问题解题策略把PQ+QB转化为PQ+QA

！当Q运动到E时，PQ+QA最小第二步

计算——勾股定理线段和差的最值问题解题策略把PQ+QB转化为PQ+QA！当线段和差的最值问题解题策略第二步

计算——勾股定理把PQ+QB转化为PQ+QA

！当Q运动到E时，PQ+QA最小线段和差的最值问题解题策略第二步计算——勾股定理把PQ+线段和差的最值问题解题策略小结E?F!线段和差的最值问题解题策略小结E?F!3.如图，∠AOB=45，角内有一动点P，PO=10，在AO，BO上有两动点Q，R，求△PQR周长的最小值。ABOPDERQ3.如图，∠AOB=45，角内有一动点P，PO=10，在A4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD（不含B点）上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证：△AMB≌△ENB；⑵①当M点在何处时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；EA

DBCNM4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为爱是什么？

一个精灵坐在碧绿的枝叶间沉思。

风儿若有若无。

一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。

精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？”

“爱。”

“为什么？”

“它驱赶我的饥饿。”

鸟儿啄完稻谷，轻轻梳理着光润的羽毛。

“现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。

鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。”

精灵摘下一片树叶，里面盛了一汪泉水。

鸟儿喝完泉水，准备振翅飞去。

“请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。

“你要去做什么更重要的事吗？我这里又稻谷也有泉水。”

“我要去那片开着风信子的山谷，去看那朵风信子。”

“为什么？它能驱赶你的饥饿？”

“不能。”

“它能滋润你的干渴？”

“不能。”爱是