高等动力学课件：lecture2_Momentum_impulsive

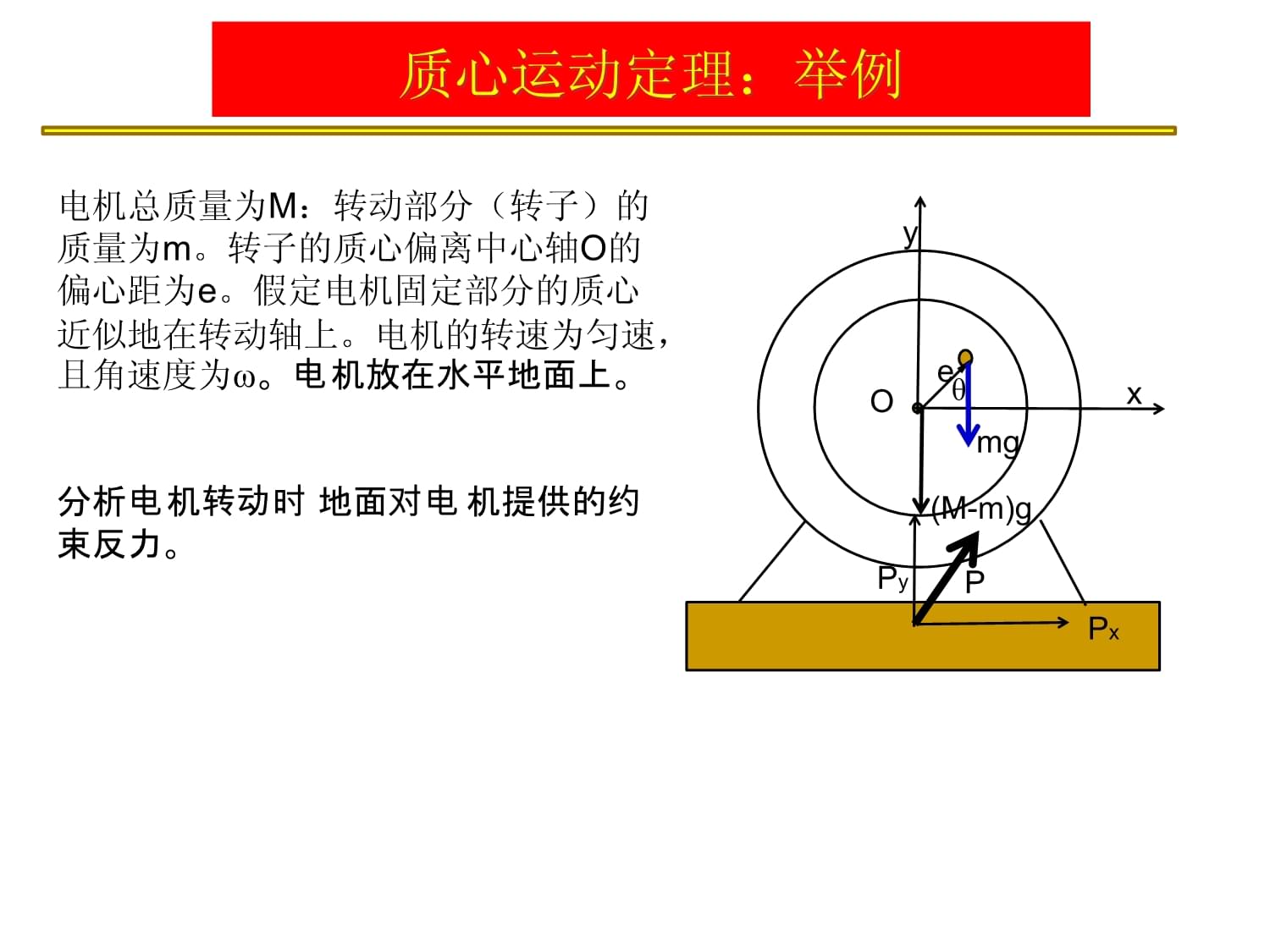
1、 Lecture 2 冲击与碰撞质心运动定理根据质心的定义，并微分质点系质心系质心的运动好象是一个质点的运动，这个质点的质量等于整个系的质量，受到的力是所有外力的主向量。 质心运动定理在平均意义上考虑质点系的运动，并大大简化了对刚体运动的处理。根据质点系的动量定理外力系的主矢量定义质心的速度质心运动定理：举例m甲m乙r乙r甲rC飞石索的运动飞石索质心的运动轨迹总是一条抛物线。爆竹、烟花等虽然可以展现丰富多彩的景象，但其在平均意义上的轨迹方程是简单的。质心运动定理：举例电机总质量为M：转动部分（转子）的质量为m。转子的质心偏离中心轴O的偏心距为e。假定电机固定部分的质心近似地在转动轴上。电机的转

2、速为匀速，且角速度为。电机放在水平地面上。分析电机转动时地面对电机提供的约束反力。exymgO(M-m)gPPxPy质心运动定理：举例分析对象：电机中的固定部分+转子质点系的质心位置应用质心运动定理分量形式物理或工程意义讨论：当e或较大时，Py可能出现负值，需要提供可承受拉力的部件。水平方向如果仅受静摩擦的作用，要求的条件为有水平振动的条件为两体问题两体问题：将各个星体之间的相互作用忽略，仅考虑太阳对星体的相互作用，这样行星的运动可以看做一个两个质点相互作用的孤立系统。分析内容：是否可以将太阳作为惯性参考系，建立其它行星的运动方程？（将两体问题转化为单体问题）应用： 航天工程中的某些轨道动力学

3、问题的分析，粒子的散射等Mm两体的质心C质心平动参考系rmrM两体问题Mm两体的质心C质心平动参考系rmrM建立质心平动参考系。质点m到质心C的位置矢量为：其中：r为M到m之间的矢量。两质点之间的相互作用力为f. 定义：则即为当以太阳作为不动点参考系时，考虑地球在万有引力作用下的折合质量。由于地球的质量远远小于太阳的质量，所以，可近似认为=1质心平动参考系为惯性参考系，质点m的动力学方程为粒子的散射rcrv1设质量为m1的质点以速度v1被一质量为m2的静止质点散射。受与距离平方呈反比的排斥力的作用，在质心坐标系中观测，粒子的散射角度为c求：实验室坐标系:静止坐标系，r粒子的散射建立质心平动参考

4、系。质心的速度方向必定沿v1的方向。质心平动参考系m1m1m2m2V1V2V2V1c质点1相对质心平动参考系的速度V1质点2相对质心平动参考系下的速度V2在质心参考坐标系中，动量守恒。故散射后质点1和2的速度方向必定沿相反方向。粒子的散射在实验室参考系。质点1散射前后的速度为v1， v1质点2散射前后的速度0， v2m1m1m2m2v1实验室坐标系v2v1rVv1V1cr两种坐标系下的速度关系：写成分量形式后，可得到粒子的散射实验室坐标系xm1rcm2Cr2r1ry根据质心的定义，有如下关系对上式微分散射后，当两质点远离到无引力场的作用时，因系统是保守的，这时两质点相对速度的大小必定与其起始时

5、两粒子的相对速度的大小相等。即：则机械能守恒条件导致的结果。由于质心速度则散射过程，在机械能保持守恒的条件下，能够使动能转移。Review for the last course质点系： 质点系：离散系统，连续系统。 关联作用的不同，构成了具有不同性态的基本模型（本构方程）。 刚体是由质点之间相对位置保持不变的无限多质点构成的一组特殊的质点系统。 质点系内力的两个性质所有内力的主向量为零所有内力对某一共同点的主矩等于零质点系的动量定理（在整体上把握系统运动的特征）微分形式积分形式质心运动定理 质心的定义（加权平均意义上的处理）冲击力冲击力的概念：一个力对作用时间的平均大小比常规力大几个数量级，

6、作用时间比常规力的作用时间小几个数量级，而冲量具有常规量的数量级。数学表述的工具（广义函数）函数（Dirac函数）广义脉冲函数数学上的广义系统：微分方程中包含函数的微分动力系统。广义函数的微分和积分运算.设存在如下的一个分段连续函数广义函数及其导数对函数F(x)分段微分xf(x)1/Heaviside函数Step fucntion同连续函数中极限的概念类似，令0。则分段函数F(x)将收敛到单位阶跃函数I(x)脉冲函数（函数）： 函数f(x)将收敛到函数1(x)与(x)函数之间的关系11(x)xHeaviside函数：(x)x函数:广义函数利用基本函数1(x)及(x)，我们便可以对一类具有分段连

7、续的函数定义相关的微分和积分运算。用广义1(x)来表示函数yx-23yx2-23+(x+2)x2-3-(x-2)+函数y的导数为：冲击力的数学表示tF+面积I力F 在时间间隔内的冲量：在趋于零时，冲击力可以表示为：根据动量定理的积分形式可以看出，动量的变化量来源于冲量。即力和时间的共同作用，才是导致质点系体的运动发生改变的重要因素。因此，在分析系统受冲击力作用时，冲量的概念具有重要的意义。tF0冲击问题分析问题：设质量为m的质点同时受到常规力F常和冲击力F(t)=I(t-)的作用，试分析质点受到冲击作用前后的运动情况。根据质点动量定理则有积分可得冲击力使质点的速度发生改变冲击过程引起的位移变化

8、是小量。常规力的作用可以忽略不计，冲击过程将在速度水平上改变质点的运动效果。冲击过程中对质点位移的改变很小，可以忽略不计。以上这些基本的结论构成了处理具有多尺度问题的数学描述手段。冲击问题举例 质量为m的质点由弹簧竖直悬挂着处于平衡状态，弹簧常数为k。给质点一个竖直向下的打击，其冲量大小为I，求:质点受打击后的运动。 冲击问题举例受力分析冲击力重力弹簧拉力动力学微分方程对冲击过程在时间间隔t=-0,+0积分冲击后的运动微分方程坐标原点的选取：平衡位置微分方程的解为质点的冲击过程如同给弹簧质量系统施加一个初始条件。举例:内冲击光滑水平面上有两个小球，质量均为m。它们用一条不可伸长的绳子相连，绳长

9、l。开始时两小球紧挨着，设小球1获得一初速u并设当绳子被拉直以后两球的速度相等。分析两个小球的运动和绳的张力。举例:内冲击假设：柔索的不可伸长约束和单边受拉性质。碰撞后两球的速度相等。动力学过程分析：具有分段和非连续特征。Phase 1: t =l/u; 质点系内部质点保持原有的运动形式不变。Phase 2: t= =l/u; 绳子张紧，设张紧过程具有微小的时间间隔-0, +0。冲击后保证两质点之间满足绳索约束。Phase 3: 冲击后，两球将保持相同的速度运动（假设绳索的刚性约束一直保持，但绳中的拉力为零。）故根据动量守恒有单个小球的冲量：T=mu(t-)/2内力：举例:内冲击冲击过程中的能

10、量变化：冲击前的动能：冲击后的动能内力对1球做的功内力对2球做的功注意：内力虽然不改变质点系统的动量，但会做功。Comments:题目中给定的冲击后两球速度相等的条件是一个很强的假定。事实上，该问题同两球的碰撞问题非常相似。举例:质点串的冲击三个质点A，B和C，质量分别为m1，m2和m3，用拉直而不可伸长的绳子AB和BC相连，静止地安放在光滑水平面上，角ABC为(-)， 是锐角。对质点C施加一冲击力，其冲量大小为I，方向沿BC。求：质点B运动的方向与AB的夹角 质点A的速度 举例:质点串的冲击ij冲击过程分析：冲击后A点的速度方向沿AB方向；冲击后C点的速度方向沿BC方向两个约束方程：冲击结束

11、时，质点A和质点B之间沿绳长方向无相对速度：质点B和质点C之间沿绳长BC方向无相对速度。设打击后A点的速度为u1,C点的速度为u3, B点的速度为(u2, v2)对质点系应用动量定理：根据以上四个方程Discussion:解题过程中给出的两个运动学补充条件是过强的假设。碰撞碰撞过程的特征（Impact or Collision） 接触点处存在强的相互作用；常规力可忽略不计构型不变速度突变系统分析：碰撞过程中的冲击力为内力，因此动量守恒。碰撞根据接触面的相互作用，显然需要在接触点处沿法向和切向分别提供独立的物理方程。切向方向：对干摩擦接触，满足库伦摩擦定律法线方向：需根据材料的性质提供相关的物性

12、方程。法向物性方程的讨论（经典碰撞动力学理论）：考虑碰撞过程可能激发的能量耗散现象，历史上通常采用恢复系数(coefficient of restitution)的概念进行描述。牛顿恢复系数特点：利用碰撞前后相对速度的变化量来反映碰撞过程中的能量耗散现象。碰撞Poisson恢复系数：认为碰撞过程可以分为两个阶段：压缩阶段和恢复阶段。压缩阶段的法向冲量为I1，恢复阶段的法向冲量为I2。特点：根据压缩和恢复阶段冲量大小的比值来反映碰撞过程中的能量耗散。能量恢复系数：仍将碰撞过程分为两个阶段，压缩和恢复。设压缩阶段法向冲击力所做的功（负功）为Wc,恢复阶段法向冲击力所作的功（正功）为WR。三种恢复系

13、数的等价性三种不同的恢复系数，在处理两个光滑质点碰撞过程中的统一性。压缩阶段与恢复阶段转化点的条件为：两质点在压缩阶段结束时的相对速度为零，即这一瞬时，两质点具有共同的速度V.根据动量定理，压缩阶段的冲量方程可表示为恢复阶段的冲量方程可表示为由以上公式，可得显然有三种恢复系数的等价性根据动量定理存在如下的动力学方程根据冲量的定义，在时间间隔0, 内的冲量为由于F总大于零，故p一定是单值函数。故上式可表示为如下的微分形式。因此，质点1和 2的动力学方程可表示为如下对新的微分变量dp的微分方程积分三种恢复系数的等价性压缩阶段结束时刻，内部冲击力所做的功设整个碰撞过程的总冲量为I，碰撞过程内力所做的功恢复阶段内部法向冲击力所做