大学物理学第五版马文蔚高等教育出版社静电场3

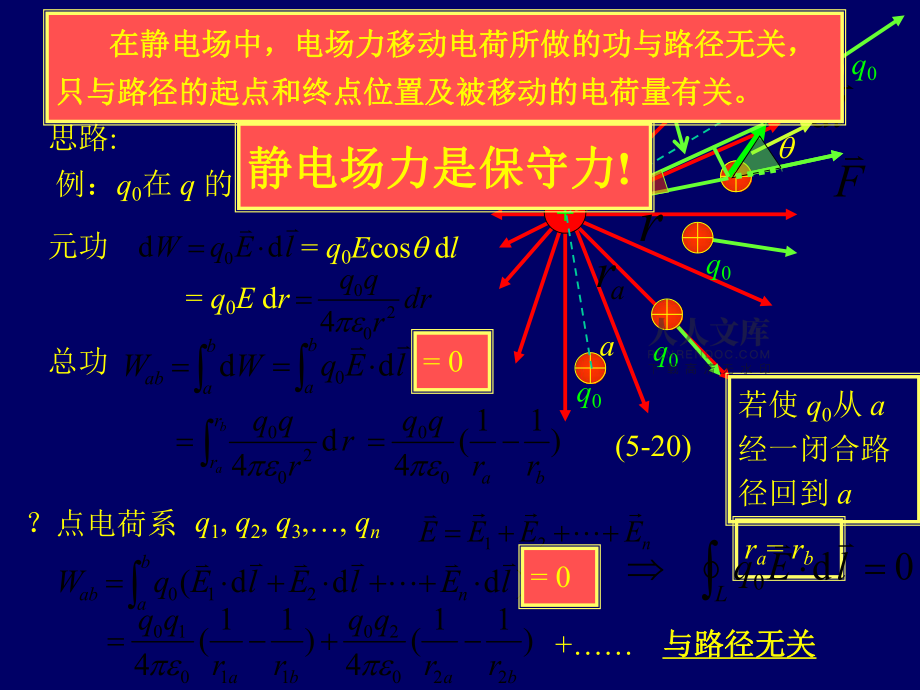
1、大 学 物 理静电场（第三讲）作业：P193 5-22 5-23 5-26 5-295-6 静电场的环路定理 电势能 一静电场力所做的功思路:例：q0在 q 的电场中移动。q+q0aarq0q0q0bbrFrld元功lEqWdd0= q0Ecos dl= q0E dr总功baabWWdbarrrrqqd4200)11(400barrqq(5-20)balEqd0？点电荷系 q1, q2, q3, qnnEEEE21banablElElEqW)ddd(210)11(411010barrqq)11(422020barrqq+与路径无关与路径无关静电场力是保守力静电场力是保守力!若使 q0从 a 经

2、一闭合路径回到 ara= rb= 0= 00d0LlEqdrrqq2004drr 在静电场中，电场力移动电荷所做的功与路径无关，在静电场中，电场力移动电荷所做的功与路径无关，只与路径的起点和终点位置及被移动的电荷量有关。只与路径的起点和终点位置及被移动的电荷量有关。q0a二静电场的环路定理0d0LlEqW0dLlE(5-23)场强的环流场强的环流静电场的环流等于静电场的环流等于 0。 静电场是保守力场。物理含义有势场三电势能保守力做功与其相应势能增量间的关系?qrarbabbaablEqWd0= (EpbEpa)=EpaEpb(5-24)电电势能也具有相对性相对性；与势能零点选择有关。带电体分

3、布在有限区域，通常取无限远处为势能 零点E p =0选零点的原则：使问题简化！取b点电势能为0Epb =0Epa =WabbalEq势能点00d(5-25)+q0在场中任一点a的电势能Epa 在量值上 = 把 q0从a点移到远处(Ep=0处处)电场力所做的功Aa注意：电势能是一个相互作用系统共有的 相互作用能。+(5-21)Epa =Aa0点00dalEq5-7 电势V (电位)回顾场强：0qF 用其比值定义0qFE而今：EpaEpa q0一.电势：势能点0dalE(5-26)E 与 V 的积分关系V的物理意义： 场中某点的V在数值上等于把单位正电荷从该点经任意路径移到电势为0处，电场力所做的

4、功。或： 单位正电荷在该处具有的电势能。V 的单位：伏特(V)说明：a) V 为标量。b) 与q0无关；由场源和场点决定。c) V 也具有相对性。 相对不同的参考零点有不同的值。一般一般 取无限远处 V=0；有时接地(取地电势)为零。选参考零点的原则：简便、有有意义意义。d) 根据电势定义知：Vp 和Ep具有相同的参考零点。Ep=q0 Vp 0qEVpaaq0电势差电势差 V ：(电压)a b V =Uab= VaVb点0dalE点0dblE点0ddbbalElE点0dblEbaablEUd)dcos(balE(5-27) 场中任意两点a、b间的 Uab在量值上等于把单位正电荷从a点经任意路径

5、到达b点时，电场力所做的功。 与电势零点的选择无关。静电场力做功的表式静电场力做功的表式q ab单位单位正电荷， 功 Uabq功 qUabWab =q(Va Vb)(5-28)(简便!注意下标顺序)推导：baablEqWdbalEqd=q(Va Vb)例一半径为 R 的均匀带电球面，带电Q。+R(1) 规定无限远处电势为 0，求球面的电势；(2) 规定球面上电势为0，求无限远处的电势。解：rRrrQRrE204)0(0(1)V=0RRlEVd沿何向沿何向?RrrQd420(2)VR=0RlEVdRdrrQ)(cos420积分至 V=0处！保持不变。任意两点的电势差与参考零点的选择无关电势差与参

6、考零点的选择无关！RQ04RQ04RQUR04 帕塞尔教授在电磁学中写道：如果从地球上移去一滴水中的所有电子，则地球的电势将会升高几百万伏。设一滴水体积为1cm3，则其质量为1g。由于水的摩尔质量为18g。这样，一滴水中的电荷量为：1923106 . 11002. 6181qC31035. 5RqV04639104 . 61035. 5109V6105 . 7 r0 当V= 0二.电势的计算方法一：按定义计算点0daalEV选择适当适当 积分路径，积到V =0处。同向或反向与 Eld即： =0或方法二： 借助点电荷点电荷 的电势公式和电势叠加原理电势叠加原理 进行计算。(1) 点电荷电场中的电

7、势q+rP (取 r= r0 处为电势零点)0drrlEVEld0d0cos420rrrrq)11(400rrq(5-29)取无穷远取无穷远 处处为电势零点？为电势零点？(5-30)q0, V 0,Vmin=V=0rVV=0q0q0, V0,Vmax=V=0q0沿电场线方向，电势逐渐降低。rqV04(2) 电势叠加原理设一点电荷系q1q2q3qn P取 V=0PPlEVdPnlEEEd)(21PnPPlElElEddd21V =V1+ V2+VnniiV1(5-31)电势叠加原理 ： 点电荷系的场中,某一点的电势等于各点电荷单独存在时在该点产生的电势的代数和。(3) 连续分布电荷电场中的电势

8、+dqrPdV元电势总总电势(5-32)积分区间： 带电体所占空间。rdqdV04rdqdVV04例1点电荷q1, q2, q3, q4均为 4.0109C，放置在一正方形的四个角顶上，各角顶与正方形中心O的距离均为 r =5.0cm 。rrrq1q2q3q4Or(1) 计算O点的电势；(2) 将试探电荷q0=1.0109C从无穷远移到O点，电场力做功多少？(3) 电势能的改变为多少？是增加还是减少？解：(1)方法一：按电势定义 方法二：按电势叠加原理OOlEVdVO = 4Vi=2.88103V电荷离散分布，用电势叠加原理求解比较方便。(2)WO= q0 (VVO)= q0VO电场力做负功(

9、3)Ep= WO = q0VO电势能增加！iirq044例2计算真空中均匀带电(q)圆环轴线上任一点的电势。+xORx解一： 按定义 xPlEVdxxEd0cos2204RxqV 好象点电荷q在 x2+R2 处产生的V。解二：按电势叠加原理计算。dl=q/2Rdq = dl元电势22xRr2204ddRxlVRVV20d2204RxqEx0R22R22Vx0E 最大处，V 不一定最大；V 最大处，E 不一定最大。23220)(4RxqxE)()(20rRrRrR220)sin()cos(4dsin2dRRrRRV例3均匀带电球面(R)电场中的 U分布。解一：用叠加原理or d (1)球内任一点

10、P1 ( rR)cos(22)cosd(d2202RrrRRV0dVV在球外：好象q全部集中在球心产生的V 似的！rVoRrEoR0RRq04)()(20RrrRrRrR02rq04r121rr p1 p2or解二：按电势定义已知：rR ,(1) rR简便简便！求电势方法小结1当电荷分布对称性不高时，用电势叠加原理简便！2当电荷分布对称性较高(或E已知)时，用电势定义简便！选取合适的积分路径（电场线），积至电势为0处！点0daalEV注意：无限大带电板、无限长带电线等不能以无穷远为零点！204rqEdrrqR204Rq04drrqVr204rq04p1p2r5-8 电场强度 与电势梯度的关系E

11、一等势面 电势分布的形象化场中 V 相等的点构成的曲面。等势面的性质：1电荷沿等势面移动时，电场力做功为0；2电场线与等势面正交。证明：1ab等势面设 q 在等势面上移动 ab，做功W=q(Va Vb)=02反证法：设 与等势面上一线元 成一 角 EldEldq将q在等势面上沿 移动ldlEqWdd= qE cos dl 0与性质与性质1矛盾！矛盾！所以， = 90lEd证毕！另外画等势面有一附加规定：场中任意相邻两等势面间的电势差相等。10V9V8V3.等势面的疏密程度可以反映场的强弱。二电场强度与电势梯度矢量矢量VV+dVdV 0nea dnEdl)(dVVVVVbaldEdVdlEcos

12、令：cosEEl方向的投影在 ldEdlEdVldldVEl物理意义：电场强度在 dl 方向的分量，等于电势沿这方向变化率的负值。nenVEdd电场中任一点场强的大小，等于该点电势沿等势面法线方向的变化率其方向与法线方向相反在直角坐标系中：(5-32)(5-33)(5-34)(5-35)kzfjyfixffgrad定义：VEgrad则： bxVExyVEyzVEznVVdd,0不一定等于零。直角坐标系中(5-35)注意注意：V(x,y,z)一定是函数表达式！并非某一点的电势值。若知V(x,y,z)，可利用(5-35) Ex, Ey, Ez, kzVjyVixVE三、场强、电势关系的应用1、定性解释现象a. 场强总是沿电势变化最快的空间方向从高电势指向低电势处。EgradVVV+dVgradV 表示沿电势增加最快的方向的一个矢量。b. 等势面越密密的地方，场强越大。c. 电势为零的地方，场强不一定零。+-oqq0, 0 EV +oqq0, 0EVxVExyVEyzVEzd. 电势不变的空间空间，场强一定为零。e. 场强的单位是伏特/米。2. 已知电势分布求场强(求导即可