【最新】中考数学复习 创新性开放性（2）课件

1、【最新】中考数学复习 创新性开放性（2）课件创新型、开放型问题创新型、开放型问题第二讲第二讲【最新】中考数学复习 创新性开放性（2）课件 第一类：找规律问题第一类：找规律问题 这类问题要求大家通过观察这类问题要求大家通过观察,分析分析,比较比较,概括概括,总结出题设反映的某总结出题设反映的某种规律种规律,进而利用这个规律解决相关进而利用这个规律解决相关问题问题【最新】中考数学复习 创新性开放性（2）课件例例1 1：观察下列算式：观察下列算式： 2 21 1=2 2=2 22 2=4 2=4 23 3=8 =8 2 24 4=16 2=16 25 5=32 2=32 26 6=64 =64 2

2、27 7=128 2=128 28 8=256=256通过观察，用你所发现的规律写出通过观察，用你所发现的规律写出8 89 9的末位数的末位数字是字是。第一列第一列第二列第二列第三列第三列第四列第四列第一行第一行2 21 1=2=22 22 2=4=42 23 3=8=82 24 4=16=16第二行第二行2 25 5=32=322 26 6=64=642 27 7=128=1282 28 8=256=256第三行第三行8例例1 1：观察下列算式：观察下列算式： 2 21 1=2 2=2 22 2=4 2=4 23 3=8 =8 2 24 4=16 2=16 25 5=32 2=32 26 6

3、=64 =64 2 27 7=128 2=128 28 8=256=256通过观察，用你所发现的规律写出通过观察，用你所发现的规律写出8 89 9的末的末位数位数字是字是。【最新】中考数学复习 创新性开放性（2）课件 第二类第二类: :探求条件问题探求条件问题 这种问题是指所给问题结论明确这种问题是指所给问题结论明确, ,而而寻求使结论成立的条件寻求使结论成立的条件. .大致有三种类型大致有三种类型 (1)(1)条件未知需探求条件未知需探求 (2)(2)条件不足条件不足需补充条件需补充条件 (3)(3)条件多余或有错条件多余或有错, ,需排需排除条件或修正错误条件除条件或修正错误条件【最新】中

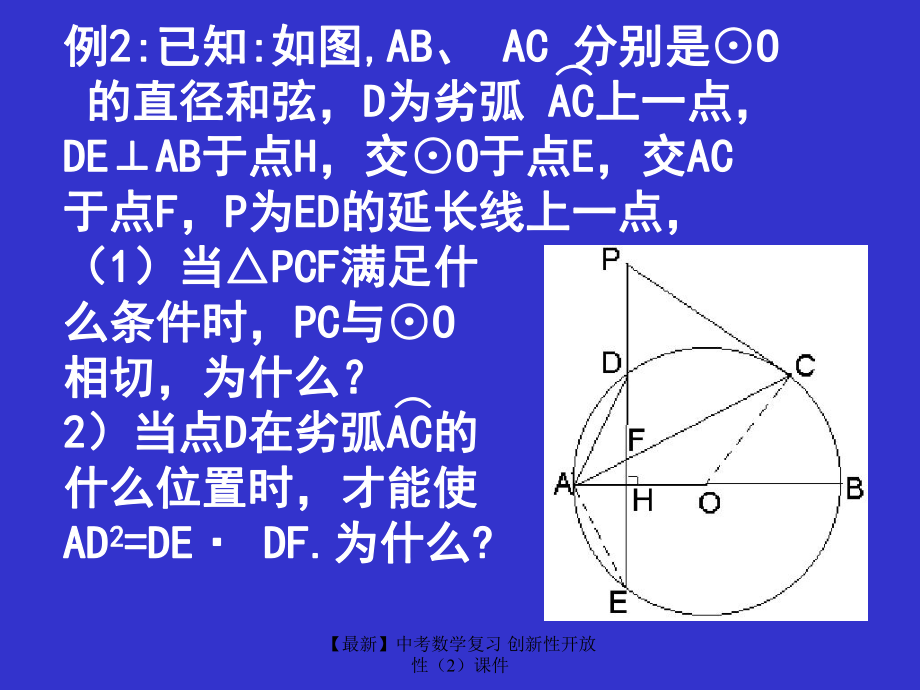
4、考数学复习 创新性开放性（2）课件例例2:2:已知已知: :如图如图,AB,AB、 AC AC 分别是分别是OO 的直径和弦，的直径和弦，D D为劣弧为劣弧 ACAC上一点，上一点，DEABDEAB于点于点H H，交，交OO于点于点E E，交，交ACAC于点于点F F，P P为为EDED的延长线上一点，的延长线上一点，（1 1）当）当PCFPCF满足什满足什么条件时，么条件时，PCPC与与OO相切，为什么？相切，为什么？2 2）当点）当点D D在劣弧在劣弧ACAC的的什么位置时，才能使什么位置时，才能使ADAD2 2=DE DF.=DE DF.为什么为什么? ? 【最新】中考数学复习 创新性开

5、放性（2）课件分析：要知分析：要知PCPC与与00相切，需知相切，需知PCOCPCOC，即，即PCO=90PCO=90，CAB+AFHCAB+AFH=90=90，而，而CAB=OCACAB=OCA，AFH=PFCAFH=PFC，PFC+OCAPFC+OCA=90=90，当当PFC=PCFPFC=PCF时，时，PCO=90PCO=90. .【最新】中考数学复习 创新性开放性（2）课件解解 :(1):(1)当当PC=PF(PC=PF(或或PCF=PFC,PCF=PFC,或或PCFPCF为等边三角形为等边三角形) )时时,PC,PC与与 OO相切相切. . 连结连结OC,OC,则则OCA=FAH.O

6、CA=FAH.PC=PF PCF=PFC=AFHPC=PF PCF=PFC=AFHDE AB DE AB OCA+PCF=FAH+AFH=90OCA+PCF=FAH+AFH=900 0即即OC PC, PCOC PC, PC与与OO相切相切. .【最新】中考数学复习 创新性开放性（2）课件（2 2）当点）当点D D在劣弧在劣弧ACAC的什么位的什么位置时，才能使置时，才能使ADAD2 2=DE DF.=DE DF.为什么为什么? ?分析分析: :要使要使ADAD2 2=DE DF=DE DF需知需知ADFADFEDAEDA证以上两三角形相证以上两三角形相似似, ,除公共角外除公共角外, ,还还

7、需证需证DAC=DEADAC=DEA故应知故应知AD=CDAD=CD 【最新】中考数学复习 创新性开放性（2）课件解：（解：（2 2）当点）当点D D是是ACAC的中点时，的中点时， ADAD2 2=DE DF.=DE DF. 连结连结AE.AE. AD=CD DAF=DEA AD=CD DAF=DEA 又又ADF=EDA ADF=EDA DAFDAFDEADEA即即ADAD2 2=DE DF=DE DFADDFDEAD 【最新】中考数学复习 创新性开放性（2）课件第三类第三类: :探求结论问题探求结论问题 这类问题是指题目中的结这类问题是指题目中的结论不确定论不确定, ,不惟一不惟一, ,或

8、结论需要或结论需要通过类比通过类比, ,引申引申, ,推广或由已知推广或由已知特殊结论特殊结论, ,归纳出一般结论归纳出一般结论【最新】中考数学复习 创新性开放性（2）课件例3：已知，O1经过O2的圆心O2，且与O2相交于A、B两点，点C为AO2B上的一动点（不运动至A、B）连结AC，并延长交O2于点P，连结BP、BC .(1)先按题意将图1补完整,然后操作,观察.图1供操作观察用,操作时可使用量角器与刻度尺.当点C在AO2B 上运动时,图中有哪些角的大小没有变化;(2)请猜想BCP的形状,并证明你的猜想(图2供证明用)(3)如图3,当PA经过点O2时,AB=4,BP交O1于D,且PB、DB的

9、长是方程x2+kx+10=0的两个根，求O1的半径的半径. 【最新】中考数学复习 创新性开放性（2）课件例3：已知，O1经过O2的圆心O2，且与O2相交于A、B两点，点C为AO2B上的一动点（不运动至A、B）连结AC，并延长交O2于点P，连结BP、BC .(1)先按题意将图1补完整,然后操作,观察.图1供操作观察用,操作时可使用量角器与刻度尺.当点C在AO2B 上运动时,图中有哪些角的大小没有变化;【最新】中考数学复习 创新性开放性（2）课件(2)请猜想BCP的形状,并证明你的猜想(图2供证明用)【最新】中考数学复习 创新性开放性（2）课件（2 2）证明：连结）证明：连结O O2 2A A、O

10、 O2 2B B，则则BOBO2 2A=ACB A=ACB BO BO2 2A=2PA=2PACB=2PACB=2PACB=P+PBCACB=P+PBCP=PBCP=PBCBCPBCP为等腰三角形为等腰三角形.【最新】中考数学复习 创新性开放性（2）课件(3)如图3,当PA经过点O2时,AB=4,BP交O1于D,且PB、DB的长是方程x2+kx+10=0的两个根，求O1的的半径半径. 【最新】中考数学复习 创新性开放性（2）课件连结连结O O2 2O O1 1并延长交并延长交ABAB于于E E，交，交OO1 1于于F F设设OO1 1、OO2 2的半径的半径分别为分别为r r、R R，OO2

11、2FABFAB，EB=1/2AB=2EB=1/2AB=2，PDBPDB、POPO2 2A A是是OO1 1的割线，的割线，PDPB=POPDPB=PO2 2PA=2RPA=2R2 2，PBPB、BDBD是方程是方程x x2 2+kx+10=0+kx+10=0的两根，的两根，PBBD=10PBBD=10，【最新】中考数学复习 创新性开放性（2）课件13EFEOEFEO2 2=AEBE=AEBE，EF=4/3EF=4/3，r=1/2r=1/2（3+4/33+4/3）=13/6=13/6OO1 1的半径为的半径为13/613/6PDPB=PDPB=（PBPBBDBD）PB=PBPB=PB2 2PBB

12、D=PBPBBD=PB2 210PB10PB2 210=2R10=2R2 2，APAP是是OO2 2的直径，的直径，PBA=90PBA=90，PBPB2 2=PA=PA2 2ABAB2 2，PBPB2 2=4R=4R2 21616得得R=R=在在RtRtO O2 2EBEB中，中，O O2 2E= E= 由相交弦定理得，由相交弦定理得，3413222 BEBO13【最新】中考数学复习 创新性开放性（2）课件第四类： 存在性问题存在性问题是指在一定件下某数学对象是否存在的问题例例4 4：抛物线：抛物线y=axy=ax2 2+ +bxbx+c+c（a a0 0）过过P P（1 1，- -2 2），

13、），Q Q（- -1,21,2），），且与且与X X轴交于轴交于A,BA,B两点两点( (A A在在B B的左的左侧侧),),与与Y Y轴交于轴交于C C点，连结点，连结ACAC，BCBC1.1. 求求a a与与c c的关系式的关系式2.2. 若若( (O O为坐标原点为坐标原点),),求抛物线的解析式求抛物线的解析式3.3.是否存在满足条件是否存在满足条件tantanCABCAB穧穧 cotcotCBA=1CBA=1的的抛物抛物线线? ?若存在若存在, , 请求出抛物线的解析式。若不存请求出抛物线的解析式。若不存在，请说明理由在，请说明理由。OCOBOA411 + +【最新】中考数学复习 创

14、新性开放性（2）课件解解（1 1）将）将P P（1 1，-2-2），），Q Q（-1-1，2 2）代入解析式得代入解析式得 解方程组得解方程组得a+c=0a+c=0，b=b=2 2 aa，c c的关系式是的关系式是a+c=0a+c=0或或a=a=c c+cbacba22【最新】中考数学复习 创新性开放性（2）课件例例4 4：抛物线：抛物线y=axy=ax2 2+bx+c+bx+c（a a0 0）过）过P P（1 1，-2-2），），Q Q（-1,2-1,2），且与），且与X X轴交于轴交于A,BA,B两点两点(A(A在在B B的左侧的左侧),),与与Y Y轴交于轴交于C C点，连结点，连结AC

15、AC，BCBC 求求a a与与c c的关系式的关系式 若若 (O(O为坐标原点为坐标原点),),求抛物线的解析式求抛物线的解析式1.1.3.3.是否存在满足条件是否存在满足条件tanCABcotCBA=1tanCABcotCBA=1的抛物线的抛物线? ?若存在若存在, , 请求出抛物线的解析式。若不存在，请请求出抛物线的解析式。若不存在，请说明理由说明理由。 OCOBOA411 + +【最新】中考数学复习 创新性开放性（2）课件（2 2）由（）由（1 1）知）知b=b=2 2，所以，所以y=axy=ax2 22x+c2x+c设设A A（x x1 1，0 0）B B（x x2 2，0 0）则）则

16、x x1 1xx2 2=c/a=c/a，但，但a=a=c c，所以所以x x1 1xx2 20 0这说明这说明A A，B B在原点两侧（在原点两侧（A A在在B B的左侧）所以的左侧）所以OA=OA=x x1 1，OB=xOB=x2 2，OC=|c|=|a|OC=|c|=|a|，已已知知 故有故有即即 平方后得平方后得 而（而（x x2 2-x-x1 1）2 2= =（x x1 1+x+x2 2）2 24x4x1 1x x2 2把把x x1 1+x+x2 2=2/a=2/a，x x1 1xx2 2= =1 1代入上式中，得到关于代入上式中，得到关于a a的方程，的方程，解方程求得解方程求得a

17、a，c c从而求出解析式从而求出解析式OCOBOA411 + +|42121axxxx 222121216)()(axxxx axx41121 + + 【最新】中考数学复习 创新性开放性（2）课件（2 2）设）设A A，B B的坐标分别为（的坐标分别为（x x1 1，0 0）, ,（x x2 2，0 0）, ,则则x x1 1，x x2 2是方程是方程 axax2 22x+c=02x+c=0的两个根的两个根 xx1 1+x+x2 2=2/a=2/a，x x1 1x x2 2= =1 1因此因此A A，B B两点分别在原点两侧，因为两点分别在原点两侧，因为A A在在B B的左侧，的左侧，所以所以

18、x x1 10 0，x x2 20 0，故，故OA=OA=x x1 1，OB=xOB=x2 2，OC=|c|=|a|OC=|c|=|a|，由，由 得得 即即 OCOBOA411 + +|42121axxxx axx41121 + + 【最新】中考数学复习 创新性开放性（2）课件平方后得平方后得 又又 于是得于是得4/a4/a2 2+4=16/a+4=16/a2 2, ,解之得解之得a= a= ，c= c= 所以解析式为所以解析式为222121216)()(axxxx （x x2 2-x-x1 1）2 2= =（x x1 1+x+x2 2）2 2 4x4x1 1x x2 232332322+ + xxyxxy33 【最新】中考数学复习 创新性开放性（2）课件例例4 4：抛物线：抛物线y=axy=ax