311方程的根与函数的零点zz

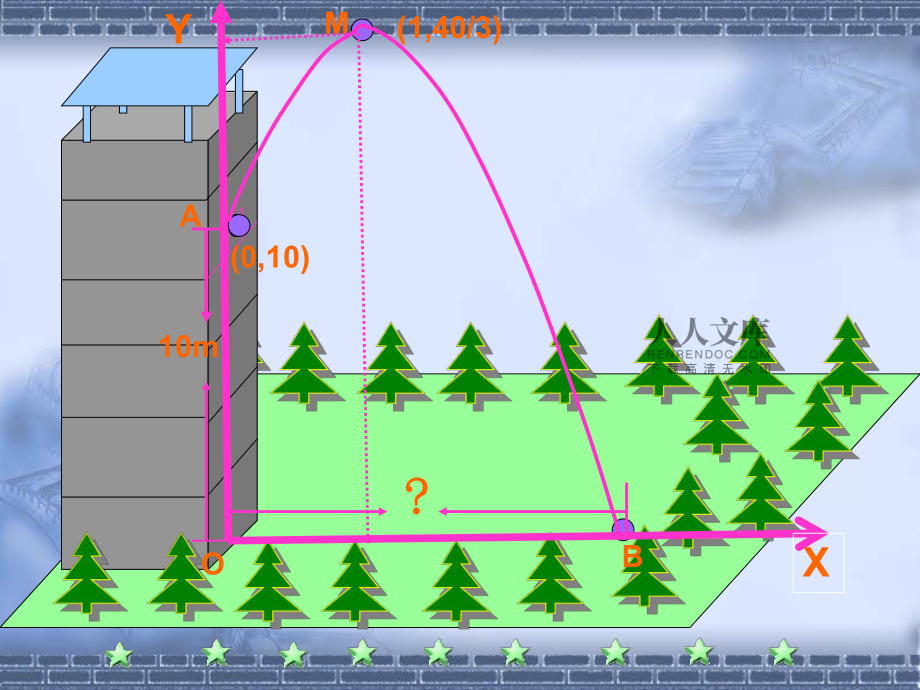
1、 方程的根方程的根 和和 函数的零点函数的零点XYAMBO10m(1,40/3)(0,10)? ? 思考：一元二次方程思考：一元二次方程ax2+bx+c=0(a0)的根与二次函数的根与二次函数y=ax2+bx+c(a0)的图象有什么关系？的图象有什么关系？ 方程方程x22x+1=0 x22x+3=0y= x22x3 y= x22x+1函数函数函函数数的的图图象象实数根实数根x1=1,x2=3x1=x2=1无实数根无实数根 图象图象与与x轴的交点轴的交点(1,0)、(3,0)(1,0)无交点无交点x22x3=0 xy01321121234.xy0132112543.yx012112y= x22x

2、+3方程方程ax2 +bx+c=0(a0)的根的根函数函数y= ax2 +bx+c(a0)的图象的图象判别式判别式 =b24ac0=00函数的图象函数的图象与与 x 轴的交点轴的交点有两个相等的有两个相等的实数根实数根x1 = x2没有没有 实实 数数 根根xyx1x20 xy0 x1xy0(x1,0) , (x2,0)(x1,0)没有没有 交交 点点两个不相等两个不相等的实数根的实数根x1 、x2 对于函数对于函数y=f(x),我们把使我们把使f(x)=0的的叫做叫做函数函数y=f(x)的的零点零点。注意：注意：零点零点指的是一个指的是一个实数实数零点是一个点吗零点是一个点吗? ?实数实数x

3、方程方程f(x)=0有有 实实 数数 根根函数函数y=f(x)的图象与的图象与x轴有轴有 交交 点点函数函数y=f(x)有有 零零 点点x x2 2-x+20-x+20； (2)y=2(2)y=2x x-1; -1; 求下列函数的零点。求下列函数的零点。评注：评注：求函数的零点就是求相应的方程的根，一般可以借助求根公式或因式分解等办法，求出方程的根，从而得出函数的零点。 问题探究问题探究观察函数的图象观察函数的图象在区间在区间(a,b)上上_(有有/无无)零点；零点；f(a).f(b)_0（或）（或） 在区间在区间(b,c)上上_(有有/无无)零零点；点；f(b).f(c) _ 0（或）（或）

4、 在区间在区间(c,d)上上_(有有/无无)零零点；点；f(c).f(d) _ 0（或）（或）0123 4 5-1-212345-1-2-3-4xy探究探究一正一负一正一负结论结论两正就无零点吗？两正就无零点吗？例例abababababb bbb bbbbbbbbbbbbxy0思考：思考：若函数若函数y=f(x) 在区间在区间(a, b)内内有零点，一定能得出有零点，一定能得出f(a)f(b)0的结的结论吗？论吗？ 有零点，唯一吗？有零点，唯一吗？ 如果函数如果函数 y=f(x) 在在a,b上上, 图象是图象是连续连续的，的， 并且在闭区间的两个端点上的函数值并且在闭区间的两个端点上的函数值 互异互异,即即f(a)f(b)0, 且是且是单调单调函数函数, 那么，这个函数在那么，这个函数在(a,b)内必有内必有惟一惟一的的一个零点。一个零点。练习练习：练习练习:B例例1 求函数求函数f(x)=