应力状态分析和强度理论

1、应力状态分析和强度理论一应力状态概述一应力状态概述1点的应力状态：点的应力状态：杆件中杆件中不同横截面不同横截面上的内力一般不相同，同一横截面上上的内力一般不相同，同一横截面上不同点不同点的应力一般不相同，的应力一般不相同，同一点同一点不同方位不同方位的截面上的应力一般不相同，这种应力情况即为点的应力状态；的截面上的应力一般不相同，这种应力情况即为点的应力状态；图图7-1围绕一点且各边是无穷小的围绕一点且各边是无穷小的正六面体正六面体称单元体；初次截取的单元体一般包括横截称单元体；初次截取的单元体一般包括横截面和纵截面；单元体各个面上的应力是面和纵截面；单元体各个面上的应力是均布均布的，平行面

2、上的的，平行面上的应力性质应力性质是相同的，是相同的，即即应力大小应力大小是相等的，正应力的指向都是拉或都是压，剪应力的方向为使单元体是相等的，正应力的指向都是拉或都是压，剪应力的方向为使单元体有相同的转向；见图有相同的转向；见图7-1；2用单元体表示点的应力状态：用单元体表示点的应力状态：一应力状态概述一应力状态概述3基本变形中点的应力状态初步分析：基本变形中点的应力状态初步分析：AN图图7-2ABPPPPABAB(1) 轴向拉伸和压缩：见图轴向拉伸和压缩：见图7-2；应力计算公式是：应力计算公式是：一应力状态概述一应力状态概述3基本变形中点的应力状态初步分析：基本变形中点的应力状态初步分析

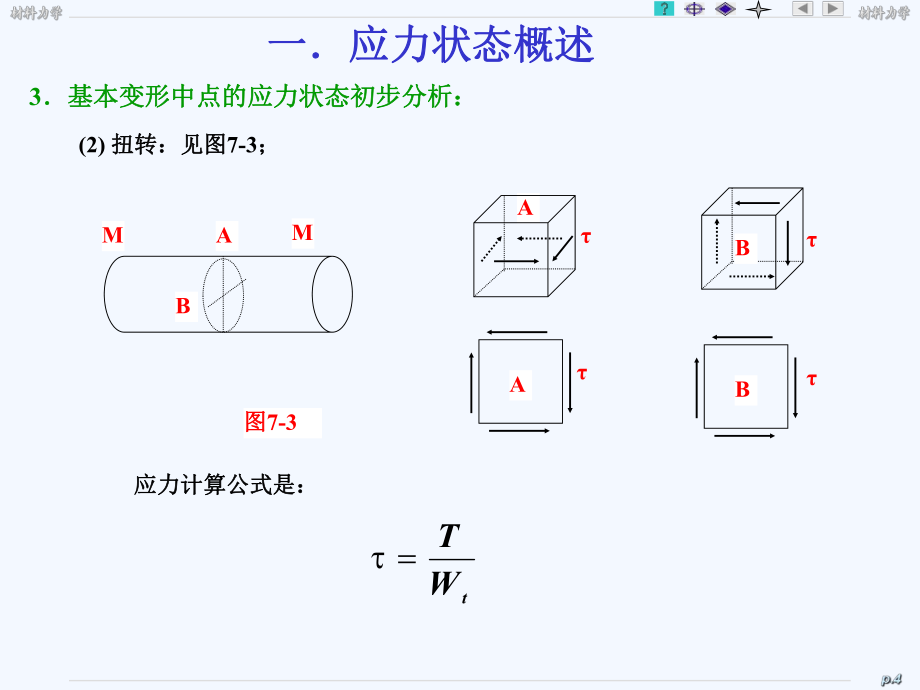
3、：应力计算公式是：应力计算公式是：tWTAABMMBAB图图7-3(2) 扭转：见图扭转：见图7-3；一应力状态概述一应力状态概述3基本变形中点的应力状态初步分析：基本变形中点的应力状态初步分析：应力计算公式是：应力计算公式是：AQkbIQSWMIMymaxZz*maxz PABCABCACB图图7-4ABCmaxmaxmaxmax(3) 弯曲：见图弯曲：见图7-4；一应力状态概述一应力状态概述4主平面和主应力：主平面和主应力：剪应力为零剪应力为零的平面为的平面为主平面主平面；主平面上的正应力称；主平面上的正应力称主应力主应力，按代数值大小，按代数值大小顺序排列分别是顺序排列分别是1 1 、2

4、 2和和3 3； 5应力状态的分类：应力状态的分类：单向应力状态：只有一个主应力不为零；单向应力状态：只有一个主应力不为零；二向应力状态：只有二个主应力不为零；二向应力状态：只有二个主应力不为零；三向应力状态：三个主应力均不为零；三向应力状态：三个主应力均不为零；二二向应力状态分析二二向应力状态分析-解析法解析法1应力分量及其符号的规定：应力分量及其符号的规定：应力分量是应力分量是x 、y和和 xy(xy和和yx大小相等大小相等)；正应力正应力规定与截面规定与截面外法线外法线方向一致为方向一致为正正，反之为负；，反之为负；剪应力剪应力规定对单元体内任一点的矩规定对单元体内任一点的矩顺顺时针为时

5、针为正正，反之为负；，反之为负；见图见图7-5；图图7-5nxxxxyyyyxyxyxyxyyxyxyxyx 二二向应力状态分析二二向应力状态分析-解析法解析法2斜截面上的应力：斜截面上的应力： 0sin)sin(cos)sin( cos)cos(sin)cos( 0dAdAdAdAdAFyyxxxynndA dAsin dAcos图图7-6xyxyyx见图见图7-6；列出平衡方程：列出平衡方程：0cos)sin(sin)sin( sin)cos(cos)cos( 0dAdAdAdAdAFyyxxxy二二向应力状态分析二二向应力状态分析-解析法解析法2斜截面上的应力：斜截面上的应力： 2222

6、222cossinsincosxyyxxyyxyx由剪应力互等定理：由剪应力互等定理： xy=yx整理得：nxyxyyx（1）二二向应力状态分析二二向应力状态分析-解析法解析法 00yxxytg22044 22200203主平面的位置：主平面的位置：取正切函数的主值：取正切函数的主值：另一个值是：另一个值是：令令nxyxyyx（2）02cos2sin2000 xyyx二二向应力状态分析二二向应力状态分析-解析法解析法 4主应力的值：主应力的值：将主平面位置的值代入正应力计算公式得：将主平面位置的值代入正应力计算公式得：2200222xyyxyxnxyxyyx（3）二二向应力状态分析二二向应力状

7、态分析-解析法解析法 5正应力的极值：正应力的极值：0dd02222cossinddxyyxyxxytg222222xyyxyxminmax令令，得，得由此可见，主应力的极值等于主应力，即由此可见，主应力的极值等于主应力，即（2）（3）nxyxyyx二二向应力状态分析二二向应力状态分析-解析法解析法 (1) 当当x y 时，主平面主值时，主平面主值 0上的应力是上的应力是max ，而，而(0+/2)上的应力上的应力min ；6正应力的极值与主平面之间的对应关系：正应力的极值与主平面之间的对应关系：(2) 当当x 0，tg= - ，则，则 0 = - /4 ，对应，对应max ；若若 xy 0，

8、tg=，则，则 0 =/4 ，对应，对应max ；二二向应力状态分析二二向应力状态分析-解析法解析法 ；01ddxyyxtg22112201tgtg4 2220101(1) 位置：令位置：令，得，得由于由于则得：则得：即即剪应力极值平面剪应力极值平面与主平面的夹角为与主平面的夹角为450；两个剪应力极值平面之间的夹角是；两个剪应力极值平面之间的夹角是900；7剪应力的极值位置和大小剪应力的极值位置和大小02sin22cos111xyyxdd二二向应力状态分析二二向应力状态分析-解析法解析法 7剪应力的极值位置和大小剪应力的极值位置和大小22minmax2xyyx2minmaxmax(2) 大小

9、：大小：这是剪应力互等定理的表达式；这是剪应力互等定理的表达式；显然有：显然有：将将1的值代入剪应力计算公式得：的值代入剪应力计算公式得：(3) 剪应力极值位置与极值大小的对应关系：剪应力极值位置与极值大小的对应关系：从从主应力极值主应力极值max的主平面的主平面逆时针转逆时针转450，得到的剪应力极值平面上是，得到的剪应力极值平面上是maxnxyxyyx（4）（5）三二向应力状态分析三二向应力状态分析-图解法图解法 ；2cos2sin22sin2cos22xyyxxyyxyx222222xyyxyx0 ,2yx222xyyx1应力圆方程：应力圆方程：二式二边平方后相加得：二式二边平方后相加得

10、：这是关于这是关于 和和 ，半径是，半径是的圆方程，圆心坐标是的圆方程，圆心坐标是由斜截面应力计算公式得：由斜截面应力计算公式得：三二向应力状态分析三二向应力状态分析-图解法图解法2应力圆：应力圆：图图7-7nxxyyyxyxxyxyG2(min)G1(max)D(x, xy)E(, )A(max,0)D(y, yx)B(min,0)202以横坐标表示正应力，纵坐标表示剪应力，画出二向应力状态的应力圆；以横坐标表示正应力，纵坐标表示剪应力，画出二向应力状态的应力圆；三二向应力状态分析三二向应力状态分析-图解法图解法3应力圆与单元体之间的对应关系应力圆与单元体之间的对应关系(2) 应力圆上的点按

11、某一方向转动应力圆上的点按某一方向转动2 角度，单元体上的面按相同方向转动角度，单元体上的面按相同方向转动角度；角度；(3) 应力圆与应力圆与轴的交点代表轴的交点代表主应力主应力；(4) 应力圆上代表主应力的点转动应力圆上代表主应力的点转动900得到剪应力极值点；单元体上主平面转动得到剪应力极值点；单元体上主平面转动450得到剪应力极值平面；得到剪应力极值平面；(1) 应力圆上的每一点对应单元体上互成应力圆上的每一点对应单元体上互成1800的二个面上的应力状态；的二个面上的应力状态；图图7-7nxxyyyxyxxyxyG2(min)G1(max)D(x, xy)E(, )A(max,0)D(y

12、, yx)B(min,0)202三二向应力状态分析三二向应力状态分析-图解法图解法图图7-8图图7-94基本变形应力状态的应力圆基本变形应力状态的应力圆(1) 轴向拉伸和压缩：见图轴向拉伸和压缩：见图7-8；(2) 扭转：见图扭转：见图7-9；三二向应力状态分析三二向应力状态分析-图解法图解法4基本变形应力状态的应力圆基本变形应力状态的应力圆(3) 弯曲：见图弯曲：见图7-10；图图7-1012431342四三向应力状态简介四三向应力状态简介231max图图7-11max123见图见图7-11；阴影内的点代表三向应力状态单元体中某一截面上的应力；阴影内的点代表三向应力状态单元体中某一截面上的应

13、力；2三向应力状态下的最大剪应力：三向应力状态下的最大剪应力：1三向应力圆：三向应力圆：从图从图7-11中可知：中可知：132五广义胡克定律五广义胡克定律图图7-12112233各向同性材料在各向同性材料在小变形小变形的情况下，当应力的情况下，当应力不超过比例极限不超过比例极限，则线应变只与正应力有关，则线应变只与正应力有关，剪应变只与剪应力有关，且由正应力引起的某一方向上的线应变可以叠加；剪应变只与剪应力有关，且由正应力引起的某一方向上的线应变可以叠加；见图见图7-12；各面是主平面的单元体，沿三个主应力方向的应变称主应变，用；各面是主平面的单元体，沿三个主应力方向的应变称主应变，用1 、2

14、和和3表示；表示；由由1 引起三个主方向的线应变为：引起三个主方向的线应变为：1应变叠加原理：应变叠加原理：2主方向上的广义胡克定律：主方向上的广义胡克定律：E,E,E113112111 五广义胡克定律五广义胡克定律图图7-12112233由由2 引起三个主方向的线应变为：引起三个主方向的线应变为：2主方向上的广义胡克定律：主方向上的广义胡克定律：EEE223222221 , ,E,E,E333332331 32131211111E叠加后得：叠加后得：这是广义胡克定律在三个主方向上的表达式；这是广义胡克定律在三个主方向上的表达式； 由由3 引起三个主方向的线应变为：引起三个主方向的线应变为：1

15、3232221221E21333231331E五广义胡克定律五广义胡克定律yxzzxzyyzyxxEEE1113一般形式的广义胡克定律：一般形式的广义胡克定律：GGGzxzxyzyzxyxy五广义胡克定律五广义胡克定律dzdydxVdxdydzdzdydxV321321111111111113211VVV32132121E3321mKEm3213321213EK对于主应力单元体，变形前的体积为：对于主应力单元体，变形前的体积为：变形后的体积为：变形后的体积为：定义体积应变为：定义体积应变为：略去高阶微量得：略去高阶微量得：将广义胡克定律的表达式代入得：将广义胡克定律的表达式代入得：定义平均应力

16、为：定义平均应力为：则有：则有：其中其中称体积弹性模量；称体积弹性模量；4体积应变：体积应变：六强度理论简介六强度理论简介材料发生强度破坏是由于应力、应变、应变能等材料发生强度破坏是由于应力、应变、应变能等某一因素某一因素引起的，与应力状态是简单还引起的，与应力状态是简单还是复杂没有关系；这些假设称为是复杂没有关系；这些假设称为强度理论强度理论；运用强度理论，可以由简单应力状态下的实；运用强度理论，可以由简单应力状态下的实验结果，建立复杂应力状态的强度条件；验结果，建立复杂应力状态的强度条件；1材料因强度不足发生破坏的基本类型材料因强度不足发生破坏的基本类型屈服破坏；屈服破坏；断裂破坏；断裂破

17、坏；2强度理论的提出：强度理论的提出： nb 1(1) 最大拉应力理论最大拉应力理论(第一强度理论第一强度理论)：发生断裂破坏的主要因素是：发生断裂破坏的主要因素是最大拉应力最大拉应力； 通过简单应力状态的实验得到断裂破坏的极限应力通过简单应力状态的实验得到断裂破坏的极限应力b，由此得到许用应力：，由此得到许用应力：它也可用于发生这种破坏形式的复杂应力状态，强度条件是：它也可用于发生这种破坏形式的复杂应力状态，强度条件是：3四种常用的强度理论四种常用的强度理论六强度理论简介六强度理论简介3四种常用的强度理论四种常用的强度理论Eb0EEbo32111 321(2) 最大伸长线应变理论最大伸长线应

18、变理论(第二强度理论第二强度理论)：发生断裂破坏的主要因素是：发生断裂破坏的主要因素是最大伸长线应变最大伸长线应变；在简单应力状态下，最大伸长线应变的极限值是：在简单应力状态下，最大伸长线应变的极限值是：它是通过简单应力状态的实验得到，将它应用于一般应力状态，即它是通过简单应力状态的实验得到，将它应用于一般应力状态，即强度条件为：强度条件为：b321六强度理论简介六强度理论简介3四种常用的强度理论四种常用的强度理论强度条件为：强度条件为：20smax22max031maxs 31(3) 最大剪应力理论最大剪应力理论(第三强度理论第三强度理论)：发生屈服破坏的主要因素是：发生屈服破坏的主要因素是最大剪