第七章椭球面上的测量计算

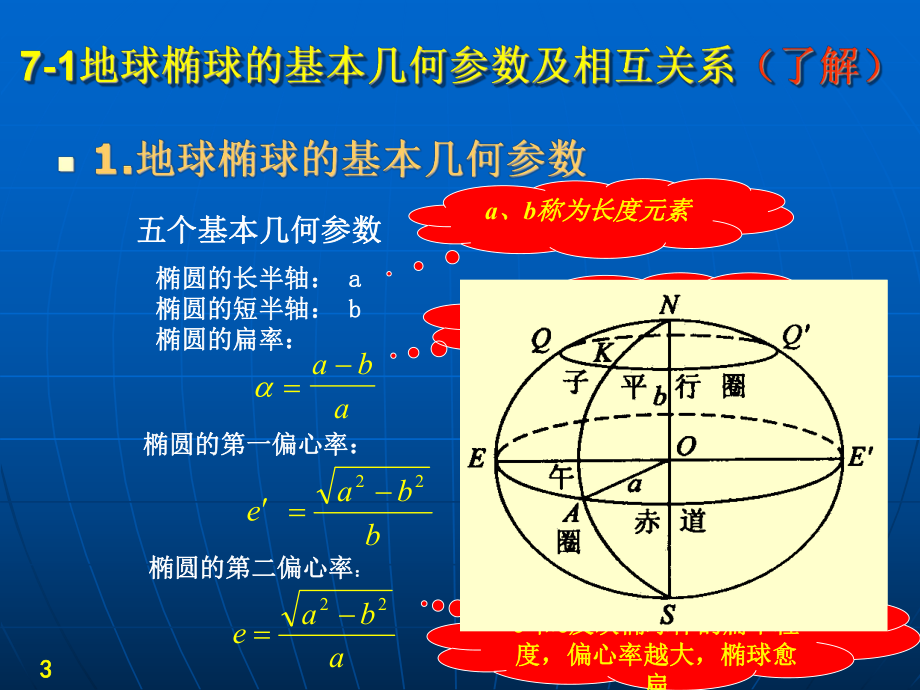
1、12 21地球椭球的定义及其几何意义； 2常用测量坐标系统的建立及其在控制测量中的应用； 3各种测量坐标系统之间的相互转换； 4椭球面上几种曲率、弧长、大地线的计算； 5地面测量值（水平方向和边长）归算到椭球面的方法。知识点及学习要求知识点及学习要求难点在对本章的学习中，有大量的公式推导与应用。各种常用测量坐标系统的建立与相互转换；几种常用的椭球计算公式；地面观测值归算到椭球面的方法与计算。 3 3椭圆的长半轴：椭圆的长半轴： a a椭圆的短半轴：椭圆的短半轴： b b椭圆的扁率：椭圆的扁率： 五个基本几何参数五个基本几何参数 aba椭圆的第一偏心率：椭圆的第一偏心率： abae22椭圆的第二

2、偏心率椭圆的第二偏心率： bbae22 a、b称为长度元素称为长度元素扁率反映了椭球体的扁率反映了椭球体的扁平程度扁平程度 e和和e反映椭球体的扁平程反映椭球体的扁平程度，偏心率越大，椭球愈度，偏心率越大，椭球愈扁扁 4 42222,tan,cosactBeBb 22221sin,1cosWeB VeB 式中，式中，W W 第一基本纬度函数，第一基本纬度函数，V V 第二基本纬度函数。第二基本纬度函数。5 5 我国所采用的的我国所采用的的19541954年北京坐标系应用的是克年北京坐标系应用的是克拉索夫斯基椭球参数；以后采用的拉索夫斯基椭球参数；以后采用的19801980国家大地坐国家大地坐标

3、系应用的是标系应用的是19751975国际椭球参数；而国际椭球参数；而GPSGPS应用的是应用的是WGS-84WGS-84系椭球参数。系椭球参数。 6 62.地球椭球参数间的相互关系地球椭球参数间的相互关系abae22bbae22 eaba2222eabb22221222eba2221aeb ()( )11122eeeee2221eee22217 7abebae1122 caeace1122 eeeeee1122221 1eVWeWV8 8大地坐标系、大地坐标系、空间直角坐标系空间直角坐标系（大地测量中两种基本坐标系）（大地测量中两种基本坐标系）子午平面直角坐标系子午平面直角坐标系大地极坐标系

4、大地极坐标系 9 9 P点的子午面点的子午面NPS与起始子与起始子午面午面NGS所构成的二面角所构成的二面角叫做叫做P点点大地经度大地经度，P点的点的法线法线Pn与赤道面的夹角与赤道面的夹角B叫叫P点的点的大地纬度大地纬度，P点的位点的位置用置用L、B表示表示 。P)()(大地水准面差距高程异常正正常NHHHH若若P点不在椭球面上，还要点不在椭球面上，还要一个参数：一个参数：大地高大地高H来表示来表示点位。它与正常高及正高的点位。它与正常高及正高的关系为：关系为：1010以椭球中心以椭球中心O为原点，起为原点，起始子午面与赤道面交线始子午面与赤道面交线为为X轴，在赤道面上与轴，在赤道面上与X轴

5、正交的方向为轴正交的方向为Y轴，椭轴，椭球体的旋转轴为球体的旋转轴为Z轴，构轴，构成右手坐标系成右手坐标系O-XYZ，在该坐标系中，在该坐标系中，P点的位点的位置用置用X、Y、Z表示表示 1111设设P点的大地经度为点的大地经度为L，在过在过P点的子午面上，点的子午面上，以子午圈椭圆中心为以子午圈椭圆中心为原点，建立原点，建立x，y平面平面直角坐标系。在该坐直角坐标系。在该坐标系中，标系中，P点的位置点的位置用用L，x，y表示表示 1212 M为椭圆体面上任意为椭圆体面上任意一点，一点，MN为过为过M点的子点的子午线，午线，S为连结为连结MP的大的大地线长，地线长，A为大地线在为大地线在M点的

6、大地方位角。以点的大地方位角。以M为极点、为极点、MN为极轴、为极轴、S为极径、为极径、A为极角，就构为极角，就构成了大地极坐标系。成了大地极坐标系。P点点位置用位置用S、A表示。表示。 椭球面上的极坐标（椭球面上的极坐标（S、A）与大地坐标（）与大地坐标（L、B）可以互相换算，这种换算叫大地主题解算。可以互相换算，这种换算叫大地主题解算。1313xaBeBaBWcossincos1222222(1)sinsin(1)sin1sinaeBabByeBWVeB 过过p p 点作法线点作法线PnPn，它，它与与x 轴之夹角为轴之夹角为B，过点作，过点作子午圈的切线子午圈的切线TP，它与，它与x 轴

7、的夹角为（轴的夹角为（9090+ +B）- -该角的正切值为曲线在该角的正切值为曲线在P P点处切线的斜率点处切线的斜率. .1414设设Pn=N，则有：，则有：yP sinB2(1)PNe2nNecosxNBcosaBxWaNW2(1)sinayeBW2(1)sinyNeB一个有用的结论推导：一个有用的结论推导：1515cos,sin,XxL YxL Zy1616X XY Y2coscoscossin(1)sinXNBLYNBLZNeBcosxNB2(1)sinyNeBcos ,sin ,XxL YxL Zy当当P P点位于椭球面上时：点位于椭球面上时：1717BHeNLBHNLBHNZYX

8、sin)1 (sincos)(coscos)(2La rc tgYXZBNeYXctgBYXBNeZtgBcossin222222或NBYXHeNBZHcos)1(sin222当当P P点不在椭球面上时：点不在椭球面上时：18181919MaeW()123221sinWeBMaeceaeMcMaec022329021111()( )()2acb2020dBdSM BdxBDEdSsinsinMdxdBB 1sin2cossinWdBdWBBWadBdxdWdBdeBdBeBBeBeBBW122 1222222sinsincossinsincosdxdBaBWeBWaBWWeB sincossi

9、n(cos)12233222cosaBxWdxdBaBWeBeB sin(sincos)322221WeB2221sindxdBaBWe sin()321221sinWeBMaeW()123MdxdBB 1sin21212、卯酉圈曲率半径、卯酉圈曲率半径 NaW221sinWeBaN 02222平行圈平面与卯平行圈平面与卯酉圈平面之间的夹角即为大地纬酉圈平面之间的夹角即为大地纬度度B B，所以有：，所以有：rNBcos平行圈半径平行圈半径r就等于就等于P点的横坐标点的横坐标x（子午（子午面直角坐标系），即：面直角坐标系），即：xraBWcosNaW23233 3、任意法截弧的曲率半径、任意法截

10、弧的曲率半径22221(1)(1cos)2coscos22ARRARReBAR222coseB 当当A=0或或180时，时，RA的值最小，此时的值最小，此时R0=M（子午曲率（子午曲率半径）当半径）当A=90或或270时，时，RA的值最大，此时的值最大，此时R90=N（卯酉圈曲率半径）；当（卯酉圈曲率半径）；当A由由090时，时，RA之值由之值由MN；当当A由由90180时，时，RA之值由之值由NM。RA值的变化是以值的变化是以90为周期且与子午圈和卯酉圈对称的。为周期且与子午圈和卯酉圈对称的。24244 4、平均曲率半径、平均曲率半径M、N、R的关系：的关系：NR M只有在极点上，它们才相等

11、，且均等于极曲率半只有在极点上，它们才相等，且均等于极曲率半径径c，即：，即： 2222(1).bcNaRMNeWVVWNRMc909090 由于由于R RA A的数值随方位的数值随方位A A的变化而变化，给测量带来不便，在测量工作中，的变化而变化，给测量带来不便，在测量工作中，往往根据一定的精度要求，在一定范围内，把椭球面当作球面来处理，为此，往往根据一定的精度要求，在一定范围内，把椭球面当作球面来处理，为此，就要推求该球面的曲率半径就要推求该球面的曲率半径-平均曲率半径平均曲率半径 就是过椭球面上一点的一切法截就是过椭球面上一点的一切法截弧弧(0(022），当其数目趋于无穷时，它们的曲率半

12、径的算术平均值的极限，），当其数目趋于无穷时，它们的曲率半径的算术平均值的极限，就称为平均曲率半径，用就称为平均曲率半径，用R R表示表示 。25257.4 椭球面上的弧长计算椭球面上的弧长计算1.1.子午线弧长计算公式子午线弧长计算公式dxMdBBeBeBe44222322sin815sin231)sin1 (sincossincoscos241212238122184BBBBB32222244433(1sin)1 (cos2 )44451515(cos2cos4 )641664eBeeBeeBeB 2300(1)BBaeXMdBdBW221sinWeB将积分因子按二项式定理展开为级数形式将

13、积分因子按二项式定理展开为级数形式将正弦的指数函数化为余弦的倍数函数将正弦的指数函数化为余弦的倍数函数 322220(1)(1sin)BaeeBdB2626BCBBBAeaX4sin42sin2)1 (232222444233451515(1sin)1 (cos2 )(cos2cos4 )44641664eBeeBeeBeB Aee134456424B42161543eeC46415eXaeABBCBdBB() (coscos)1242027272.平行圈弧长公式平行圈弧长公式 cos llSrNB 旋转椭球体的平行圈是一个圆，其半径就是圆上任意一点的旋转椭球体的平行圈是一个圆，其半径就是圆上

14、任意一点的子午面直角坐标子午面直角坐标x：22coscos1sinaBrxNBeB如果平行圈上有两点，其经如果平行圈上有两点，其经差差 ，可写出平行圈弧长公式：可写出平行圈弧长公式： 12 LLl 28283.子午线弧长和平行圈弧长变化的比较子午线弧长和平行圈弧长变化的比较B 1 单位纬差的子午线弧长随单位纬差的子午线弧长随B B的增大而缓慢地增大；而单位的增大而缓慢地增大；而单位经差的平行圈弧长则随经差的平行圈弧长则随B B的增大而急剧缩短。同时还知，子午的增大而急剧缩短。同时还知，子午弧长弧长1 1约为约为110KM110KM，11约为约为1.8KM1.8KM，11约为约为30M30M；而

15、平行圈；而平行圈弧长仅在赤道附近才与子午线弧长大体相当，随着弧长仅在赤道附近才与子午线弧长大体相当，随着B B的增大它的增大它们的差值愈来愈大。们的差值愈来愈大。29297.5 大地线大地线 1.相对法截线的概念相对法截线的概念 （1）纬度不同的两点，法线必）纬度不同的两点，法线必交于旋转轴的不同点；交于旋转轴的不同点；（2）椭球面上一点的纬度愈高，）椭球面上一点的纬度愈高，法线与旋转轴的交点愈低；法线与旋转轴的交点愈低；（3）当两点的纬度不同，又不）当两点的纬度不同，又不在同一子午圈上时，这两点的法在同一子午圈上时，这两点的法线将在空间交错而不相交。因此线将在空间交错而不相交。因此当两点不在

16、同一子午圈上，也不当两点不在同一子午圈上，也不在同一平行圈上时，两点间就有在同一平行圈上时，两点间就有二条法截线存在。二条法截线存在。首先明确以下三点：首先明确以下三点：3030ABnb假定经纬仪的纵轴同假定经纬仪的纵轴同A，B两点的两点的法线重合（忽略垂线偏差），如法线重合（忽略垂线偏差），如此以两点为测站，则经纬仪的照此以两点为测站，则经纬仪的照准面就是准面就是法截面法截面。用用A点照准点照准B点，点，则照准面则照准面 同椭球面的截线同椭球面的截线为为 ，叫做，叫做A点的点的正法截线正法截线，或或B点的点的反法截线反法截线；同理，由；同理，由B照照A点，则照准面点，则照准面 同椭球面的同椭

17、球面的截线为截线为BbA ，叫做，叫做B点的点的正法截线正法截线，或或A点的点的反法截线反法截线。因。因A，B的法的法线互不相交，故这两条法截线不线互不相交，故这两条法截线不重合。我们把重合。我们把 和和BbA叫做叫做A、B两点的两点的相对法截线。相对法截线。 BAnaAaBAaB3131当当A A、B B两点位于同一子午圈或同两点位于同一子午圈或同一平行圈上时，正反法截线则合一平行圈上时，正反法截线则合二为一，这是一种特殊情况。而二为一，这是一种特殊情况。而通常情况下，正反法截线是不重通常情况下，正反法截线是不重合的。因此在椭球面上合的。因此在椭球面上A A、B B、C C三点处所测得的角度

18、三点处所测得的角度（各点上正（各点上正法截线之夹角）法截线之夹角）将不能构成闭合将不能构成闭合三角形。为克服这个矛盾，在两三角形。为克服这个矛盾，在两点间另选一条单一的点间另选一条单一的大地线大地线代代替相对法截线，从而得到由大地替相对法截线，从而得到由大地线构成的单一的三角形。线构成的单一的三角形。32322、大地线的定义和性质、大地线的定义和性质 椭球面上两点间的最短曲线椭球面上两点间的最短曲线叫做叫做大地线大地线。大地线是椭球面上两点间唯一最短线，大地线是椭球面上两点间唯一最短线，而且位于相对法截线之间，并靠近正而且位于相对法截线之间，并靠近正法截线，它与法截线，它与正正法截线间的夹角为

19、：法截线间的夹角为： 13在一等三角测量中，在一等三角测量中，可达千分之四秒，可达千分之四秒，可达千分之一二秒可达千分之一二秒 33333、大地线的微分方程和克莱洛、大地线的微分方程和克莱洛(克莱劳克莱劳)方程方程 dBAMdScosdSBNAdlcossin1）大地线微分方程）大地线微分方程: 表达表达dL，dB，dA与与dS的关系式。的关系式。MdBdSAcosAdSBdlNsincosdA PTr dl cossinsinrdlNBdlAdABdltgBdSPTNctgBNPTNctgB3434dBAMdScossin AdAtgBdSNBNBdBMAAdAcossincossincos

20、sinrNBMBdBdr rdrctgAdAlnsinlnlnArCrACsin代入代入两边积分得：两边积分得：麦尼儿定理：麦尼儿定理：3535rACsin1221sinsinAArr上式表明：在旋转椭球面上，大地线各点的平行圈上式表明：在旋转椭球面上，大地线各点的平行圈半径与大地线在该点的大地方位角的正弦的乘积等半径与大地线在该点的大地方位角的正弦的乘积等于常数。于常数。 利用这个关系式可以检查利用这个关系式可以检查纬度与方位角计算的正确纬度与方位角计算的正确性性coscosaBxrNBW36367.6 7.6 将地面观测的方向值归算到椭球面将地面观测的方向值归算到椭球面 （重点）（重点）

21、1 1、将地面观测的水平方向归算至椭球面、将地面观测的水平方向归算至椭球面-三差改正三差改正 归算中两个基本要求：归算中两个基本要求：（1）以椭球面的法线为基准；）以椭球面的法线为基准；（2）将地面观测元素化为椭球面上大地线的相应元素。）将地面观测元素化为椭球面上大地线的相应元素。 将水平方向归算至椭球面，包括垂线偏差改正、标高差将水平方向归算至椭球面，包括垂线偏差改正、标高差改正及截面差改正，习惯上称此三项为改正及截面差改正，习惯上称此三项为三差改正。三差改正。37371)cossin(ctgZAAmmu 1)cossin(tgAAmm垂线偏差改正的计算公式垂线偏差改正的计算公式 u1）垂线

22、偏差改正）垂线偏差改正 把以垂线为依据的地面观测的水平方向值归算到以法线把以垂线为依据的地面观测的水平方向值归算到以法线为依据的方向值而应加的改正数称为为依据的方向值而应加的改正数称为垂线偏差改正垂线偏差改正。3838h标高差改正：由照准点高度引起的改正标高差改正：由照准点高度引起的改正前面已得出结论：不在同一子午面或不前面已得出结论：不在同一子午面或不在同一平行圈上的两点的法线是不共面在同一平行圈上的两点的法线是不共面的。因此，当进行水平方向观测时，如的。因此，当进行水平方向观测时，如果照准点高出椭球面某一高度，则照准果照准点高出椭球面某一高度，则照准面就不能通过照准点的法线同椭球面的面就不

23、能通过照准点的法线同椭球面的交点，由此引起的方向偏差的改正称标交点，由此引起的方向偏差的改正称标高差改正，以高差改正，以 表示。表示。 h1222222sincos) 1 (2ABHe 22(1)/MaHH常2222221cos) 1 (2BHeK 112sinAKh 照准点大地纬度照准点大地纬度 测站点至照准点的大地方位角测站点至照准点的大地方位角 与照准点的纬度与照准点的纬度B B2 2对对应的子午圈曲率半径应的子午圈曲率半径 照准点的觇标高照准点的觇标高 标高差改正主要与照准点的标高差改正主要与照准点的高程有关。高程有关。 3939g3 3）截面差改正）截面差改正将法截弧方向化为大地线方

24、向应加的改正叫将法截弧方向化为大地线方向应加的改正叫截面差改正截面差改正 11221222sincos)2(12ABSeg 11(2)N1221222cos)2(12BSeK 122sinAKg 测站点大地纬度测站点大地纬度 与测站点的纬度与测站点的纬度B B1 1对应的对应的 卯酉圈曲率半径卯酉圈曲率半径 截面差改正主要与测站点至照准点截面差改正主要与测站点至照准点间的距离间的距离S S有关。有关。4040各等三角测量在归算时对取位的要求：各等三角测量在归算时对取位的要求： 一等需算至一等需算至0.0010.001； 二等为二等为0.010.01； 三等和四等为三等和四等为0.10.1。 在

25、一般情况下，一等三角测量应加三差改正；二等三角在一般情况下，一等三角测量应加三差改正；二等三角测量应加垂线偏差改正和标高改正，而不加截面差改正；三测量应加垂线偏差改正和标高改正，而不加截面差改正；三等和四等三角测量只有在等和四等三角测量只有在 或或H2000mH2000m时，才分时，才分别考虑加垂线偏差改正和标高差改正。别考虑加垂线偏差改正和标高差改正。 01 41412 2、将天文方位角归化为大地方位角、将天文方位角归化为大地方位角-起始方位角起始方位角（了解）（了解） ()sinuAL背景：背景：在布设国家天文大地网时，为了控制三角网中方位角传算误差的积累，要在布设国家天文大地网时，为了控

26、制三角网中方位角传算误差的积累，要求在一等三角锁的两端和中央，以及二等网的中间等处，都要在起始边的两个端点求在一等三角锁的两端和中央，以及二等网的中间等处，都要在起始边的两个端点上，用天文观测的方法测定它们的天文经度、天文纬度和该边的天文方位角上，用天文观测的方法测定它们的天文经度、天文纬度和该边的天文方位角( (包含测包含测站垂线的子午面与测站垂线和照准面所张成的垂直面的夹角站垂线的子午面与测站垂线和照准面所张成的垂直面的夹角) ) 。在特种工程测量控。在特种工程测量控制网中，有时也有这样的要求。天文方位角是以测站的垂线为依据的，因此必须将制网中，有时也有这样的要求。天文方位角是以测站的垂线

27、为依据的，因此必须将它归算至椭球面以测站点相应的法线为依据的大地方位角它归算至椭球面以测站点相应的法线为依据的大地方位角A A，这种归算又称起始方位，这种归算又称起始方位角的归算。角的归算。 测站点到照准点的大地方位角测站点到照准点的大地方位角测站点处相应方向的天文方位角测站点处相应方向的天文方位角测站点的天文经度测站点的天文经度测站点的大地经度测站点的大地经度测站点的天文纬度测站点的天文纬度垂线偏差改正数垂线偏差改正数 当照准点目标高度不大时，天顶距当照准点目标高度不大时，天顶距Z Z接近于接近于9090时，垂线偏差改正数可勿略时，垂线偏差改正数可勿略不计，因此上式可写为：不计，因此上式可写

28、为： ()sinAL 上式又称为上式又称为拉普拉斯方程式拉普拉斯方程式，大地方位角又叫拉普拉斯方位角，大地方位角又叫拉普拉斯方位角，在三角点上观测天文经度、天文纬度时，该点叫拉普拉斯点。在三角点上观测天文经度、天文纬度时，该点叫拉普拉斯点。 42423 3、观测天顶距受垂线偏差影响的改正、观测天顶距受垂线偏差影响的改正（了解）（了解）AAzuzzsincos11 11 11 AAzuzzsincos22 22 22 AAusincos 垂线偏差在测线上的分量：垂线偏差在测线上的分量：A为测站点至照准点的大地方位角。为测站点至照准点的大地方位角。 大地天顶距大地天顶距21ZZ 和的计算公式的计算

29、公式 利用上式公式计算出的大地天顶距利用上式公式计算出的大地天顶距Z Z可用于计算高差，此可用于计算高差，此高差称为高差称为大地高差。大地高差。三角高程测量的精度是有限的，若提高三角高程测量的精度是有限的，若提高其计算精度，必须设法克服大气折光的影响，同时要在天顶其计算精度，必须设法克服大气折光的影响，同时要在天顶观测值中引入垂线偏差改正数。观测值中引入垂线偏差改正数。 43437.7 将地面观测的长度归算到椭球面将地面观测的长度归算到椭球面（重点）（重点）1 1、基线尺量距的归算、基线尺量距的归算 )(22122121HHuuhuusu 1）垂线偏差对长度归算的影响）垂线偏差对长度归算的影响

30、 :在基线端点在基线端点1和和2处处垂线偏差在基线方垂线偏差在基线方向上的分量向上的分量 各个测段各个测段测量的高测量的高差总和差总和 基线端点基线端点1和和2处的大处的大地高地高 垂线偏差对长度归算的影响垂线偏差对长度归算的影响高程对长度归算的影响高程对长度归算的影响此项改正数值一般比较小，是否需要应结合测区及计算此项改正数值一般比较小，是否需要应结合测区及计算精度要求的实际情况进行具体分析。精度要求的实际情况进行具体分析。44442 2）高程对长度归算的影响：）高程对长度归算的影响：RHRHRSSmm1010)1(RHSSm基线两端点平基线两端点平均大地高程均大地高程 基线方向法截基线方向

31、法截线曲率半径线曲率半径 )1 (220RHRHSSmm将上式展开级数，取至二次项将上式展开级数，取至二次项 20002mmHHHSSSSSRR)(2)1 (122110HHuuRHSSm 45452 2、电磁波测距的归算、电磁波测距的归算 前提：前提：1) 在椭球面上两点间大地线长度与相在椭球面上两点间大地线长度与相应法截线长度之差是极微小的，故可忽略不计，应法截线长度之差是极微小的，故可忽略不计，这样可将两点间的法截线长度认为是该两点间的这样可将两点间的法截线长度认为是该两点间的大地线长度；大地线长度；2) 两点间的法截线长度与半径等两点间的法截线长度与半径等于其起始点曲率半径的圆弧长相差

32、也很微小于其起始点曲率半径的圆弧长相差也很微小(如如当当S=640KM时，之差等于时，之差等于0.3米；米；S=200KM时，之差等于时，之差等于0.005m)。由于工程。由于工程测量中边长一般为几公里，最长也不过十几公里，测量中边长一般为几公里，最长也不过十几公里，因而，这种差异又可忽略不计。因此所求的大地因而，这种差异又可忽略不计。因此所求的大地线长度可以认为是半径线长度可以认为是半径RA相应的圆弧长。相应的圆弧长。 232121224)1)(1 ()(1AAARDRHRHDHHDS46462322421AAmRDRHDDhDS由于控制点由于控制点之高差引起之高差引起的倾斜改正的倾斜改正的

33、主项，经的主项，经过此项改正，过此项改正，测线已变成测线已变成平距。平距。由于平均测由于平均测线高出参考线高出参考椭球面而引椭球面而引起的投影改起的投影改正，经过此正，经过此项改正后，项改正后，测线已变为测线已变为弦线。弦线。是由弦长改是由弦长改化为弧长的化为弧长的改正项。改正项。)1)(1 ()(121212AARHRHDHHDd简化后：简化后：47477.8 椭球面上三角形的解算椭球面上三角形的解算（重点）（重点）1、用勒让德尔定理解算球面三角形、用勒让德尔定理解算球面三角形 假设：假设：半径为半径为140KM范围内的椭球面可当作球面上的一范围内的椭球面可当作球面上的一部分看待。计算表明：当三角形