中考数学（人教版五四学制）巩固复习第二十九章反比例函数（含解析）

1、.2019备战中考数学人教版五四学制稳固复习-第二十九章反比例函数含解析一、单项选择题1.如图，点P3a，a是反比例函y=k0与O的一个交点，图中阴影部分的面积为10，那么反比例函数的解析式为A.yB.yC.y=D.y2.一个直角三角形的两直角边长分别为 ，其面积为2，那么表示 与 之间关系的图象大致为 A.B.C.D.不符合题意3.如图，在平面直角坐标系中，点A、B均在函数 k0，x0的图象上，A与x轴相切，B与y轴相切假设点B的坐标为1，6，A的半径是B的半径的2倍，那么点A的坐标为 A.2，2B.2，3C.3， 2D.4， 4.反比例函数y=， 以下结论中不正确的选项是 A.图象经过点，

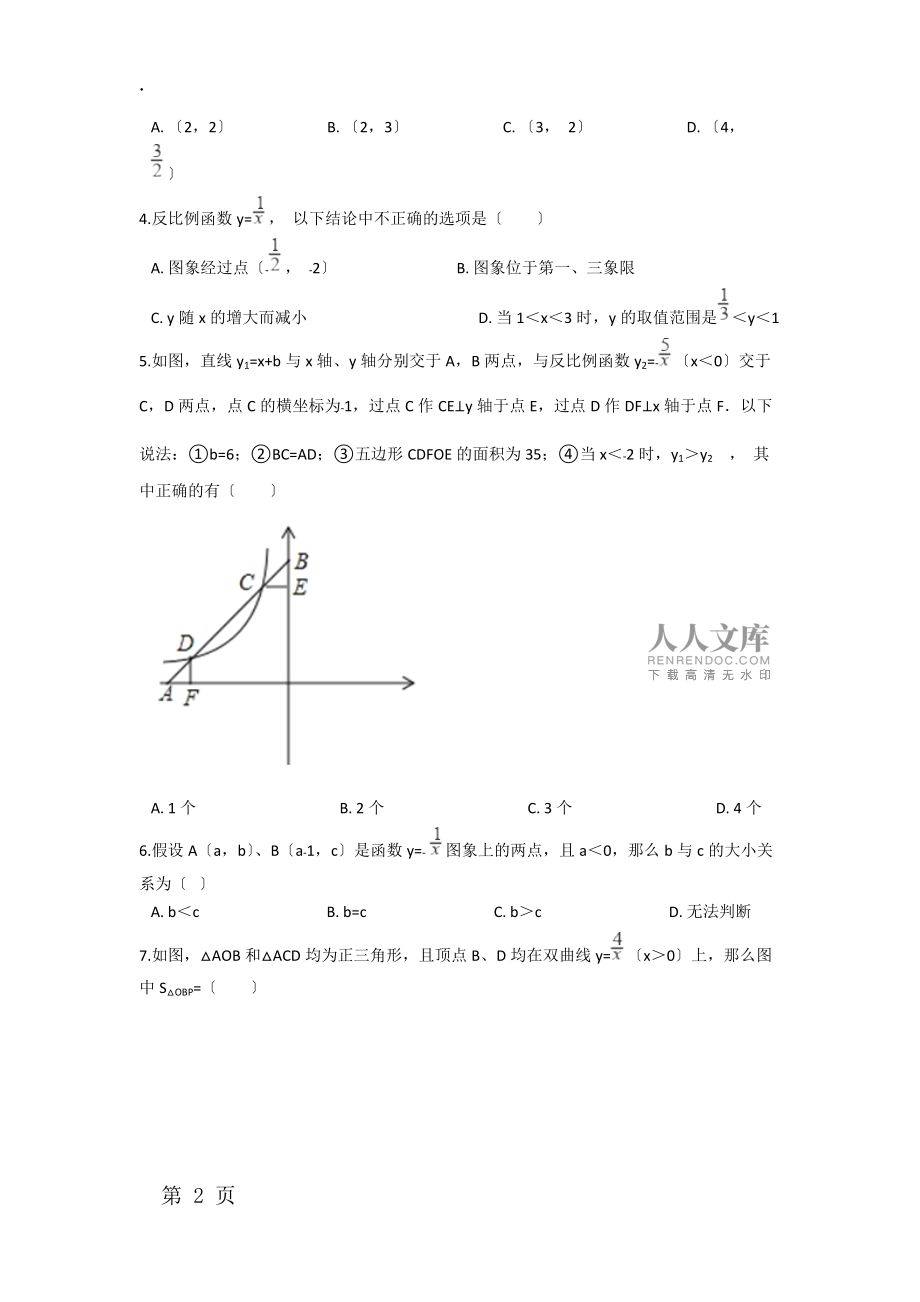
2、 2B.图象位于第一、三象限C.y随x的增大而减小D.当1x3时，y的取值范围是y15.如图，直线y1=x+b与x轴、y轴分别交于A，B两点，与反比例函数y2=x0交于C，D两点，点C的横坐标为1，过点C作CEy轴于点E，过点D作DFx轴于点F以下说法：b=6；BC=AD；五边形CDFOE的面积为35；当x2时，y1y2 ， 其中正确的有A.1个B.2个C.3个D.4个6.假设Aa，b、Ba1，c是函数y= 图象上的两点，且a0，那么b与c的大小关系为 A.bcB.b=cC.bcD.无法判断7.如图，AOB和ACD均为正三角形，且顶点B、D均在双曲线y=x0上，那么图中SOBP=A.B.C.D

3、.48.如图为反比例函数y=的图象，那么k等于A.B.C.10D.109.假设反比例函数y= k0的图象经过点1，2，那么这个函数的图象一点经过 A.2，1B. ，2C.2，1D. ，210.反比例函数y 的图象如下图，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，假如SMON=2，那么k的值为 A.2B.-2C.4D.-411.点A-1，5在反比例函数y= k0的图象上，那么该函数的解析式为 A.y= B.y= C.y=- D.y=5x12.一次函数y=ax+b与反比例函数y=图象交于M、N两点，那么不等式ax+b解集为A.x2B.1x0C.1x0或0x2D.x2或1x0二、填空题13

4、.反比例函数y= x0的图象经过矩形ABCD边BC的中点F，交CD于点E，四边形AFCE的面积为2，那么k的值为_ 14.假设y是x的反比例函数，x是z的正比例函数，那么y是z的_函数 15.如图，点A，D是函数y= k0，x0图象上两点点A在点D的左侧，直线AD分别交x，y轴于点E，FABx轴于点B，CDx轴于点C，连结AO，BD假设BC=OB+CE，SAOF+SCDE=1，那么SABD=_ 16.假设反比例函数y= 的图像经过点2，3，那么k=_ 17.如图，两个反比例函数y=和y=的图象分别是l1和l2 设点P在l1上，PCx轴，垂足为C，交l2于点A，PDy轴，垂足为D，交l2于点B，

5、那么PAB的面积为_18.函数y1=xx0，y2= x0的图象如图，有以下结论： 两函数图象的交点A的坐标为3，3；当x3时，y2y1；BC=4；当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小其中正确的结论有_19.如图，点A，C在反比例函数y= a0的图象上，点B，D在反比例函数y= b0的图象上，ABCDx轴，AB，CD在x轴的两侧，AB=3，CD=2，AB与CD的间隔 为5，那么ab的值是_ 20.在反比例函数y= 的图象上有两点Ax1 ， y1，Bx2 ， y2，当x10x2时，有y1y2 ， 那么m的取值范围是_ 21.如图，点A，C在反比例函数y= a0的图像上，点

6、B，D在反比例函数y= b0的图像上，ABCDx轴，AB，CD在x轴的两侧，AB=5，CD=4，AB与CD的间隔 为6，那么ab的值是_三、解答题22.假设反比例函数y=m25在每一个象限内，y随x的增大而增大求m的值 23.在平面直角坐标系和第一象限中有一矩形ABCD，AD平行于x轴，其中点A3，4且AB=2，BC=3假设将矩形ABCD向左平移a个单位之后，矩形到了第二象限，这时B、D两点在同一双曲线y=上1请直接写出平移前B与D两点的坐标；2试求a与k的值24.函数y=y1y2 ， y1与x成反比例，y2与x成正比例，且当x=1时，y=10；当x=3时，y=6求y与x的函数关系式 四、综合

7、题25.直线y= x与双曲线y= 的交点A的横坐标为2 1求k的值 2如图，过点Pm，3m0作x轴的垂线交双曲线y= x0于点M，交直线OA于点N 连接OM，当OA=OM时，直接写出PNPM的值试比较PM与PN的大小，并证明你的结论 26.如图，反比例函数 的图像与一次函数 的图像交于A、B两点A 2，n，B 1求反比例函数和一次函数的解析式； 2求AOB的面积； 3请结合图像直接写出当y1y2时自变量x的取值范围 答案解析部分一、单项选择题1.【答案】C 【考点】反比例函数图象的对称性 【解析】【解答】设圆的半径是r，根据圆的对称性以及反比例函数的对称性可得：r2=10解得：r=2 点P3a

8、，a是反比例函y=k0与O的一个交点3a2=k且=ra2=22=4k=34=12，那么反比例函数的解析式是：y= 应选C【分析】根据圆的对称性以及反比例函数的对称性可得，阴影部分的面积等于圆的面积的 1 4 ，即可求得圆的半径，再根据P在反比例函数的图象上，以及在圆上，即可求得k的值此题主要考察反比例函数图象的对称性的知识点，解决此题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系2.【答案】C 【考点】反比例函数的应用 【解析】【解答】直角三角形的两直角边长分别为 ，且面积为2 即 y与x之间的函数图象为反比例函数，且 图象位于一、三象限又根据x 、y实际意义可知x0、y0，其图象在

9、第一象限.故答案为：C.【分析】根据直角三角形的两直角边长分别为 x ， y ，且面积为2，可写出y与x之间的函数关系为反比例函数，又根据x 、y实际意义可知其图象在第一象限.3.【答案】C 【考点】反比例函数的性质 【解析】【解答】把B的坐标为1，6代入反比例函数解析式得：k=6，那么函数的解析式是：y= ，B的坐标为1，6，B与y轴相切，B的半径是1，那么A是2，把y=2代入y= 得：x=3，那么函数的解析式是：y= 6 x ，A的坐标是3，2故答案为：C【分析】由B的坐标1，6易得k=6，从而得到函数的解析式是：y=，再由半径关系得到A的纵坐标为2，最后代入解析式最后得到A的坐标。4.【

10、答案】C 【考点】反比例函数的性质 【解析】【解答】解：A、2=1，因此反比例函数y=经过点， 2，说法正确，故此选项不合题意；B、反比例函数y=， 图象位于第一、三象限，说法正确，故此选项不合题意；C、反比例函数y=， 在每一个象限内，y随x的增大而减小，原题说法错误，故此选项符合题意；D、当1x3时，y的取值范围是y1，说法正确，故此选项不合题意；应选：C【分析】根据反比例函数的性质：反比例函数y=k0的图象是双曲线；当k0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；当k0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大但凡反比例函数图象上的点

11、，横纵坐标之积=k进展分析即可5.【答案】B 【考点】反比例函数的应用 【解析】【解答】解：由反比例函数y2=x0经过C，点C的横坐标为1，得y=5，即C1，5反比例函数与一次函数交于C、D点，5=1+b，解得b=6，故正确；CEy轴于E点，E0，5，BE=65=1反比例函数与一次函数交于C、D点，联立 ， x2+6x+5=0解得x1=5，x2=1，当x=5时，y=5+6=1，即D5，1，即DF=1，在ADF和CBE中， ADFCBEAAS，AD=BC，故正确；作CGx轴，SCDFOE=S梯形DFGC+S矩形CGOE=+15=17，故错误；由一次函数图象在反比例函数图象上方的部分，得5x1，即

12、当5x1时，y1y2 ， 故错误；应选：B【分析】根据函数值与相应自变量的关系，可得C点坐标，根据待定系数法，可得一次函数解析式，可得答案；根据解方程组，可得C、D点的坐标，根据全等三角形的断定与性质，可得答案；根据图形的分割，可得梯形、矩形，根据面积的和差，可得答案根据函数与不等式的关系：函数图象在上方的函数值大，可得答案6.【答案】C 【考点】反比例函数的性质 【解析】【解答】a0，a10，aa1，k=10，在图象的每一支上，y随x的增大而增大，Aa，b、Ba1，c是函数y= 图象上的两点，bc，故答案为：C【分析】根据反比例函数的性质k=10时，得到在图象的每一支上，y随x的增大而增大；

13、由aa1，得到bc.7.【答案】D 【考点】反比例函数的应用 【解析】【解答】解：AOB和ACD均为正三角形，AOB=CAD=60，ADOB，SABP=SAOP ， SOBP=SAOB ， 过点B作BEOA于点E，那么SOBE=SABE=SAOB ， 点B在反比例函数y=的图象上，SOBE=4=2，SOBP=SAOB=2SOBE=4应选D【分析】先根据AOB和ACD均为正三角形可知AOB=CAD=60，故可得出ADOB，所以SABP=SAOP ， 故SOBP=SAOB ， 过点B作BEOA于点E，由反比例函数系数k的几何意义即可得出结论8.【答案】C 【考点】待定系数法求反比例函数解析式 【解

14、析】【分析】直接把点2，5代入反比例函数y=即可求得结果。【解答】反比例函数y=的图象经过点2，5k=-2-5=10.应选C.【点评】待定系数法求函数关系式是函数问题中极为重要的一种方法，在中考中极为常见，在各种题型中均有出现.9.【答案】A 【考点】反比例函数图象上点的坐标特征 【解析】【解答】解：反比例函数y= k0的图象经过点1，2， k=12=2A、21=2，这个函数的图象一点经过2，1；B、 2=12，这个函数的图象一点不经过 ，2；C、21=22，这个函数的图象一点不经过2，1；D、 2=12，这个函数的图象一点不经过 ，2；应选A【分析】先利用待定系数法求出反比例函数比例系数k的

15、值，再根据反比例函数图象上点的坐标特征求解即可10.【答案】D 【考点】反比例函数系数k的几何意义 【解析】【分析】根据反比例函数图象上的点的横纵坐标之积是定值k，同时|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积即可解答【解答】由图象上的点所构成的三角形面积为可知，该点的横纵坐标的乘积绝对值为4，又因为点M在第二象限内，所以可知反比例函数的系数为k=-4应选D【点评】此题主要考察反比例函数的比例系数k的几何意义反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系，即S=|k|11.【答案】C 【考点】待定系数法求反比例函数解析式 【解析】【解答

16、】把点的坐标代入解析式可得，k=-5故答案为：C【分析】将点A-1，5的坐标代入反比例函数解析式即可求出k=-5，可求出反比例函数的解析式。12.【答案】D 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：由图可知，x2或1x0时，ax+b 应选D【分析】根据函数图象写出一次函数图象在反比例函数图象上方部分的x的取值范围即可二、填空题13.【答案】2 【考点】反比例函数系数k的几何意义，反比例函数图象上点的坐标特征 【解析】【解答】解：反比例函数y= x0的图象经过矩形ABCD边BC的中点F， 设点F的坐标为m， ，那么点Bm，0，点Cm， ，令y= x0中y= ，那么x= ，点E

17、 ， S四边形AFCE=S梯形AECBSAFB= m +m k=2，k=2故答案为：2【分析】根据点F在反比例函数图象上，设点F的坐标为m， ，那么点Bm，0，点Cm， ，再将y= 代入反比例函数解析式中求出点E的坐标，通过分割图形求面积法即可得出关于k的一元一次方程，解方程即可得出结论14.【答案】反比例 【考点】反比例函数的定义 【解析】【解答】解：因为y是x的反比例函数，所以y=，又因为x是z的正比例函数，所以x=k2z，所以y=，即y是z的反比例函数故答案为：反比例【分析】此题可以根据正比例与反比例函数的定义确定y与z的函数关系15.【答案】【考点】反比例函数系数k的几何意义 【解析】

18、【解答】解：设Aa， ，Dd， ，那么da，Ba，0，Cd，0， BC=da，BC=OB+CE，OE=2BC=2d2a，E2d2a，0tanAEB= = = ， = = ，整理得3a24ad+d2=0，ad3ad=0，ad0，3ad=0，d=3a = ，OF= SAOF+SCDE=1， a+ 2d2ad =1，k= ，SABD=S梯形ABCDSBCD= + da da= da= 3aa= 故答案为 【分析】设Aa， ，Dd， ，那么da，Ba，0，Cd，0，由BC=OB+CE，得E2d2a，0根据tanAEB= = = ，得出 = = ，求出d=3a，OF= ，根据SAOF+SCDE=1，得到

19、 a+ 2d2ad =1，将d=3a代入求出k= ，根据SABD=S梯形ABCDSBCD即可求解16.【答案】6 【考点】反比例函数图象上点的坐标特征 【解析】【解答】解：反比例函数y= 的图像经过点2，3，3= ，解得，k=6，故答案为：6【分析】把点A2，3代入y= 求得k的值即可17.【答案】【考点】反比例函数系数k的几何意义 【解析】【解答】解：点P在y=上，|xp|yp|=|k|=1，设P的坐标是a，a为正数，PAx轴，A的横坐标是a，A在y=上，A的坐标是a，PBy轴，B的纵坐标是， B在y=上，代入得：=， 解得：x=2a，B的坐标是2a，PA=|=， PB=|a2a|=3a，P

20、Ax轴，PBy轴，x轴y轴，PAPB，PAB的面积是：PAPB=3a=故答案为： 【分析】设P的坐标是a，推出A的坐标和B的坐标，求出APB=90，求出PA、PB的值，根据三角形的面积公式求出即可18.【答案】 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：由题意可得， x0解得，x=3，将x=3代入y1=x，得y1=3，两函数图象的交点A的坐标为3，3，故正确；由图象可知，当x3时，y1y2 ， 故错误；将y=1.5代入y1=x得，x=1.5，将x=1.5代入y2= 得，y2=6，BC=61.5=4.5，故错误；由图象可知，当x逐渐增大时，y1随着x的增大而增大，y2随着x的增

21、大而减小，故正确；故答案为：【分析】根据题意可以求得两函数图象的交点A的坐标，从而可以判断；根据点A的坐标可以判断；根据点B的纵坐标可以分别求出点B、C的坐标，从而可以得到BC的值，从而可以判断；根据函数图象可以判断19.【答案】6 【考点】反比例函数系数k的几何意义 【解析】【解答】解：如图，由题意知： ab=2OE，ab=3OF，又OE+OF=5，OE=3，OF=2，ab=6故答案是：6【分析】利用反比例函数k的几何意义，结合相关线段的长度来求ab的值20.【答案】m 【考点】反比例函数的性质 【解析】【解答】反比例函数y= 的图象上有两点Ax1 ， y1，Bx2 ， y2，当x10x2时

22、，有y1y2 ， 1+2m0，故m的取值范围是：m 故答案为：【分析】由反比例函数的性质可知此反比例函数的图象在一三象限，故1+2m0，可解出m的范围.21.【答案】【考点】反比例函数的图象，反比例函数的性质 【解析】【解答】解：由题意知：ab=4OE，ab=5OF，OE= ，OF= ，又OE+OF=6， + =6，ab= ，故答案为 【分析】利用反比例函数k的几何意义得出ab=4OE，ab=5OF，求出 + =6，即可求出答案三、解答题22.【答案】解：根据题意，得m250，m2m7=1，m1=3不符合题意，舍，m2=2，m=2 【考点】反比例函数的定义 【解析】【分析】根据反比例函数的图象

23、在在每一个象限内，y随x的增大而增大，可得m250，m2m7=1，根据一元二次方程与不等式，可得答案23.【答案】解：1B3，2，D6，4；2矩形ABCD向左平移a个单位之后，矩形到了第二象限，B点的对应点的坐标为3a，2，D点的对应点的坐标为6a，4，B点和D点的对应点都在反比例函数y=的图象上，23a=46a，a=9，B6，2，k=62=12 【考点】反比例函数图象上点的坐标特征 【解析】【分析】1根据矩形的性质和点的坐标的表示方法易得平移前B与D两点的坐标；2根据点平移的规律确定平移后B与D两点的坐标，分别为3a，2、6a，4，那么利用反比例函数图象上点的坐标特征得到23a=46a，然后解方程求出a的值，再计算k的值24.【答案】解：y1与x成正比例，设y1=k1x，y2与x成反比例，设y2=，y=y1y2 ， y=k1x，x=1时，y=10，x=3时，y=6 解得：y与x的函数关系式为y=x+ 【考点】反比例函数系数k的几何意义 【解析】【分析】根据正比例函数和反比例函数定义可得y1=k1x，y2=， 进而可得y=k1x+， 再把x=1时，y=10；当x=3时，y=6代入可得关于k1、k2的方程组，解方程组可得k1、k2的值，