



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、血药浓度问题摘 要药物进入机体随备注输送到各器官中,不断被吸收、分布、代谢、最终排出,药物在血液中的浓度,称为血药浓度。针对问题一,在只有中心室的条件下,运用微分的数学思想,建立了一次给药时血药浓度关于时间的微分方程模型。按照快速静脉注射、恒速静脉滴注和口服或肌肉注射3种给药方式,不同的初值对应微分方程不同的解,分别得到3种给药方式下血药浓度随时间变化的表达式,如式,式,式根据某种药物血药浓度随时间变化的数据,利用最小二乘法进行曲线拟合,解出此药物动力学参数。利用matlab编程分别画出3种情况下的血药浓度曲线图,如图2、图3、图5所示,反映了血药浓度随时间递减或波动递减的趋势。针对问题二,在
2、快速静脉注射、恒速静脉滴注和口服或肌肉注射3种多次重复给药方式下,采用问题一中一次给药方式下的血药浓度与时间的表达式,的方法计算出多次给药方式下血药浓度表达式,一样利用matlab画出血药浓度曲线的图形。通过控制变量法,依据相关资料分别赋予时间间隔和给药剂量不同的值,画出多组血药浓度随时间变化的曲线图进行分析、比较。联系具体实际情况,即可对给药时间间隔与给药剂量的确定提供指导。通过分析不同的给药方式下的中心室内血药浓度随时间变化的规律,得到药效与给药方式、给药剂量以及给药时间间隔之间的关系,一室模型可推广到多室模型,更准确的描述血药浓度的变化规律。关键词:药物分布;快速静脉注射;恒速静脉点滴;
3、口服药或肌注;血药浓度 一、问题重述1.1问题分析药物动力学(pharmacokinetics) 亦称药动学,系应用动力学原理与数学模式,定量地描述与概括药物通过各种途径(如静脉注射,静脉滴注,口服给药等)进入体内的吸收、分布、代谢和消除,即吸收、分布、代谢、消除过程的“量-时”变化或“血药浓度-时”变化的动态规律的一门科学。药物动力学研究各种体液、组织和排泄物中药物的代谢产物水平与时间关系的过程,并研究为提出解释这些数据的模型所需要的数学关系式。房室模型 药动学通常用房室 模拟人体,只要体内某些部位接或消除药物的速率相似,即可归入一个房室,房室模型仅是进行药动学分析的一种抽象概念,并不一定代
4、表某一特定解剖部位把机体划分为一个或多个独立单元,可对药物在体内吸收、分布、消除的特性作出模式图,以建立数学模型,揭示其动态变化规律。假设机体给药后,药物立即在全身各部位达支动态平衡,这时把整个机体视为一个房室,称为一室模型或单室模型注:一房室模型虽然准确性稍差,却比较简单,便于理解、推广、应用,且有些药物用单室模型处理已能满足要求,所以其重要性并不亚于二室模型。1.2提出问题问题一,模仿5.4节建立的二室模型来建立一室模型(只有中心室),在快速静脉注射、恒速静脉滴注(持续时间为 )和口服或肌肉注射3种给药方式下求解血药浓度,并画出血药浓度曲线的图形.问题二,利用上题建立的一室模型,讨论按固定
5、时间间隔T,每次给予固定剂量D的多次重复给药方式为了维持药品的疗效和保证机体的安全,要求血药浓度c控制在(c1,c2)范围内设已知中心室容积为V(1)多次重复给药方式下,写出血药浓度表达式并作图,讨论怎样确定T和D使血药浓度的变化满足上述要求。(2)在恒速静脉滴注和口服(或肌肉注射)的多次重复给药方式下,给出血药浓度变化的简图,并在这两种方式选择一种来讨论确定T和D的问题。(3)根据所建立的模型和所得结论,给出数值仿真。二、模型假设假设中心室容积不变;假设药物从体外进入中心室,又从中心室排出体外;假设药物向体外排出的速率与该室的血药浓度成正比;假设血药在中心室中分布均匀;三、符号说明f0 表示
6、进药速率c(t) 表示浓度Cmax 表示最大浓度Cmin 表示最大浓度x(t) 表示药量v 表示容积D 注射时刻药量D1 注射过后药量k 表示排出速率系数k(0) 表示进药速率T 表示进药时间间隔s 表示恒速静脉注射持续时间四、模型的建立和求解4.1问题一的模型建立和求解按照快速静脉注射、恒速静脉滴注和口服或肌肉注射3种给药方式,不同的初值对应微分方程不同的解,分别得到3种给药方式下血药浓度随时间变化的表达式,运用matlab求解画出三种方式血药浓度随时间变化的曲线图。4.1.1模型建立考虑中心室内药物含量随时间变化的关系,建立两者之间关系的微分方程。快速静脉注射、恒速静脉滴注、口服或肌肉注射
7、这三种不同的给药方式是微分方程在不同初值条件下的特解,其中药物含量的变化由该时刻注入的药量和中心室排除的药量组成,变化过程如图1所示: F0 中心室kC(t) x(t)给药 V 排出图14.1.2模型解决中心室内药物含量随时间变化的微分方程为:= x(t)=f0(t)-kx(t) 运用常微分方程相关知识解出中心室内药物含量与时间变化的关系式x(t)=f0(t)-kx 又由于血药浓度等于药物含量与中心室体积之比,即: c(t) =x(t)/v 由和可计算出中心室内血药浓度随时间变化的关系式c(t)=f0(t)/v-kc(0) 解得:c(t)=ce-kt(1)当快速静
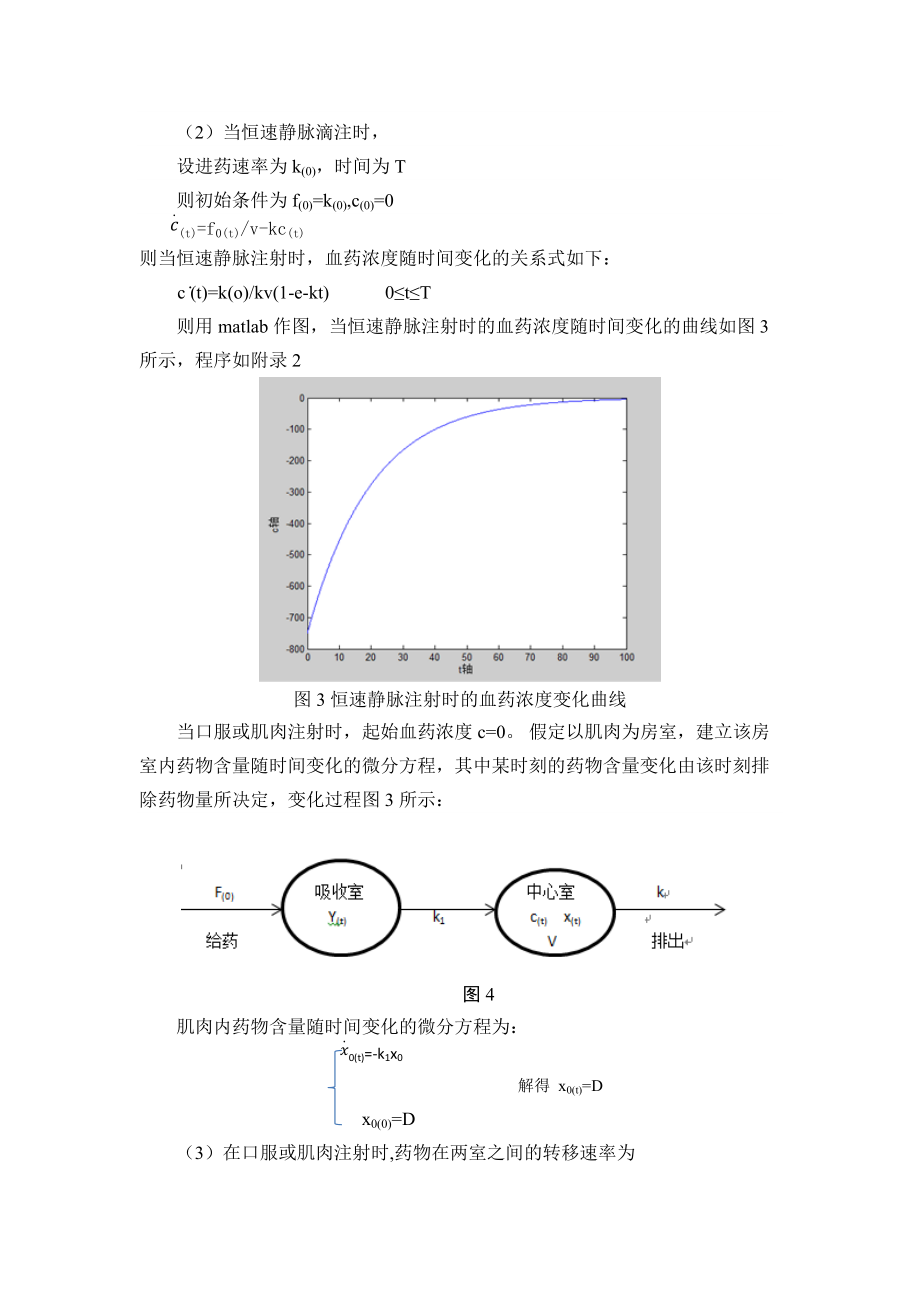
8、脉注射时设瞬时注射药量为D(0),则初始条件为c(t)=D(0)/vf0(t)=0 则当快速静脉注射时血药浓度随时间变化的关系式为:c(t)=D(0)/ve-kt 因此,当快速静脉注射时,利用matlab作图血药浓度随时间的变化曲线如图2所示,程序如附录1图2一剂量快速脉冲注射时血药浓度变化曲线(2)当恒速静脉滴注时, 设进药速率为k(0),时间为T则初始条件为f(0)=k(0),c(0)=0 c(t)=f0(t)/v-kc(t)则当恒速静脉注射时,血药浓度随时间变化的关系式如下:c (t)=k(o)/kv(1-e-kt) 0tT 则用matlab作图,当恒速静脉注射时的血药浓度随时间变化的曲
9、线如图3所示,程序如附录2图3恒速静脉注射时的血药浓度变化曲线当口服或肌肉注射时,起始血药浓度c=0。 假定以肌肉为房室,建立该房室内药物含量随时间变化的微分方程,其中某时刻的药物含量变化由该时刻排除药物量所决定,变化过程图3所示:图4肌肉内药物含量随时间变化的微分方程为: x0(t)=-k1x0 解得 x0(t)=D x0(0)=D(3)在口服或肌肉注射时,药物在两室之间的转移速率为 f0(t)=k1De-k1t 初始条件: c(o)=0因此,在口服或肌肉注射时的血药浓度与时间的关系式:c(t)=k1t/v(k(1)-k)(e-kt-e-k1t) 则用matlab作图,血药浓度随时
10、间变化的曲线如图5所示,程序如附录3图5口服或肌肉注射时血药浓度变化曲线快速静脉注射的多次重复给药方式下,在上述一次给药模型的基础上利用迭代得出表达式,从而确定给药时间间隔和剂量。4.2问题二的解决4.2.1多剂量快速静脉注射当给药方式为多剂量快速静脉注射时:根据一剂量注射,得到关系式即 在第一次注射时c(t)=D/V,(t=0).第一次注射后中心室血药浓度为,(t=T1) 第二次注射时中心室血药浓度为 在第二次注射后,中心室血药浓度为 第三次注射时中心室血药浓度为.第n次注射时中心室血药浓度为对于此式可以用等比数列求和公式求解,求解结果为 根据题目要求要使血药浓度在(c1,c2)区间,由公式
11、可以看出刚注射时浓度最大,注射后变小,则血药浓度峰值应最大为c2且 要满足要求则必须使得最大浓度cmax<c2,最小浓度cmin>c1则求得注射药量的时间间隔方程为 因此利用matlab作血药浓度随时间变化的曲线图如图6所示,程序如附录4图6多剂量快速注射时血药浓度随时间变化的曲线综上,多次给药后,血药浓度随时会见的增加达到动态平衡,得到给药时间间隔T,首次给药量D0,首次后的给药量D1,使药效达到最好。4.2.2多剂量恒速静脉滴注多剂量恒速静脉注射时第一次给药,t时的浓度为 0<tsc1(t)= s<tT第n次给药,t时的血药浓度为 nT<tnT+scn(t)=
12、 nT+s<t(n+1)T当n趋于无穷大时,血药浓度达到稳定状,则要使药物有效,则因使cminc1,cmaxc2,取cmin=c1,cmax=c2 得到则给药时间间隔为给药剂量为浓度随时间变化的图如图7,程序如附录5图7多剂量恒速注射时血药浓度变化曲线综上可得出最佳给药时间间隔T以及最佳给药量D2在多次口服或肌肉注射的情况下,血液浓度随时间变化的简图如图8所示,程序如附录6图8多剂量口服或肌肉注射血药浓度变化曲线五、模型的评价与分析首先,一房室模型虽然准确性稍差,却比较简单,便于理解、推广、应用,且有些药物用单室模型处理已能满足要求,所以其重要性并不亚于二室模型,因此,一室模型也同样重要
13、。当要求精度较高时,可采用二室甚至多室模型,例如:二室模型图如图6所示。这时的机理分析和参数估计都比一室模型难度更大。需要建立微分方程组来进行分析。图6六、参考文献1李汉龙等数学建模入门与提高,北京:国防工业出版社,20132蒋经国现代药物动力学,北京:人民卫生出版社,2011 附录Matlab程序如下附录1t=0:0.1;10;y=exp(t);plot(t,y);t=0:0.1:10; c=10.*exp(-2.*t); plot(t,c,'r-'); xlabel('t轴'); ylabel('c轴'
14、);附录2t=0:0.1:100;k=0.05;v=50;k0=0.75;c=k0*(1-exp(-k*t)/k*v);plot(t,c);xlabel('t轴'); ylabel('c轴');附录3t=0:0.1:6; c=(10.*(exp(3.*t)./2)- 1)./(3.*exp(2.*t); plot(t,c,'k-'); xlabel('tÖá');legend('c',);附录4t=0:0.01:6; c=(
15、7.*exp(-0.5.*t).*(t<2)+(8.5.*exp(-0.5.*(t-2).*(t>=2&t<4)+(10.*exp(-0.5.*(t-4).*(t>=4); plot(t,c,'k'); xlabel('t轴'); ylabel('c轴'); >> t=0:0.01:6; 附录5t=0:0.01:8; a=3.*(1-exp(-1); b=0.52934867188896155058013915022633;
16、 c=(3.*(1-exp(-0.5.*t).*(t<2)+(3-3.*exp(-1).*exp(-0.5.*(t-2).*(t>=2&t<4)+(3.*(1-exp(-0.5.*(t-4+b).*(t>=4&t<5.5)+(3-3.*exp(-1).*exp(-0.5.*(t-5.5).*(t>=5.5); plot(t,c,'k'); xlabel('t轴'); ylabel('c轴'); axis equal; set(gca,'xtick',0:0:0); set(gca,'ytick',0:0:0); 口 附录6t=0:0.01:8; a=3.*(1-exp(-1); b=0.52934867188896155058013915022633; c=(3.*(1-exp(-0.5.*t).*(t<2)+(3-3.*exp(-1).*exp(-0.5.*(t-2).*(t>=2&t<4)+(3.*(1-exp(-0
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2026中能建西北城市建设有限公司社会成熟型人才招聘笔试备考试题及答案解析
- 2026湖北恩施州来凤县国投集团招聘人员5人笔试备考题库及答案解析
- 2026天津城投集团安泊科技有限公司招聘1人考试重点试题及答案解析
- 2026宁夏银川市西夏区第二十二幼儿园招聘2人笔试备考题库及答案解析
- 2026四川华丰科技股份有限公司招聘生产计划等岗位6人考试重点题库及答案解析
- 2026年闽江学院单招综合素质笔试备考试题含详细答案解析
- 2026年泰州职业技术学院单招职业技能考试备考试题含详细答案解析
- 2026天津市博文中学初中部教师招聘2人笔试备考试题及答案解析
- 2026吴忠赛马新型建材有限公司招聘2人笔试备考题库及答案解析
- 2026山东日照市东港区新东港控股集团有限公司职业经理人招聘1人笔试备考题库及答案解析
- NB-SH-T 0945-2017 合成有机酯型电气绝缘液 含2025年第1号修改单
- 2026年细胞治疗 免疫性疾病治疗项目商业计划书
- 化工复产安全培训
- NBT 11898-2025《绿色电力消费评价技术规范》
- 2026年总经理工作计划
- 四年级数学(三位数乘两位数)计算题专项练习及答案
- 肋骨骨折护理查房
- 家具制造工艺流程及质量检验标准
- 《老年视功能衰退评估规范》
- 项目资金预警管理办法
- 社会不教、精英不讲坎儿还得自己过(揭秘人才成长规律)

评论
0/150
提交评论