422圆与圆的位置关系

1、直线与圆有几种位置关系？我们可以直线与圆有几种位置关系？我们可以怎样判断直线与圆的位置关系？怎样判断直线与圆的位置关系？CldddCCEFd r直线直线 l与与 A相交相交直线直线 l是是 A的的割线割线两个两个公共点公共点直线直线 l与与 A相切相切d r直线直线 l是是 A的的切线切线唯一唯一公共公共点点点点C是是切点切点直线直线 l与与 A相离相离d r没有没有公共点公共点 我们若把我们若把“直线直线”换成换成“圆圆”，两，两圆的位置关系会是怎样呢？需用那圆的位置关系会是怎样呢？需用那些量可以表示它们的位置关系呢？些量可以表示它们的位置关系呢？思考：思考：类比直线与圆的位置关系，想一想在

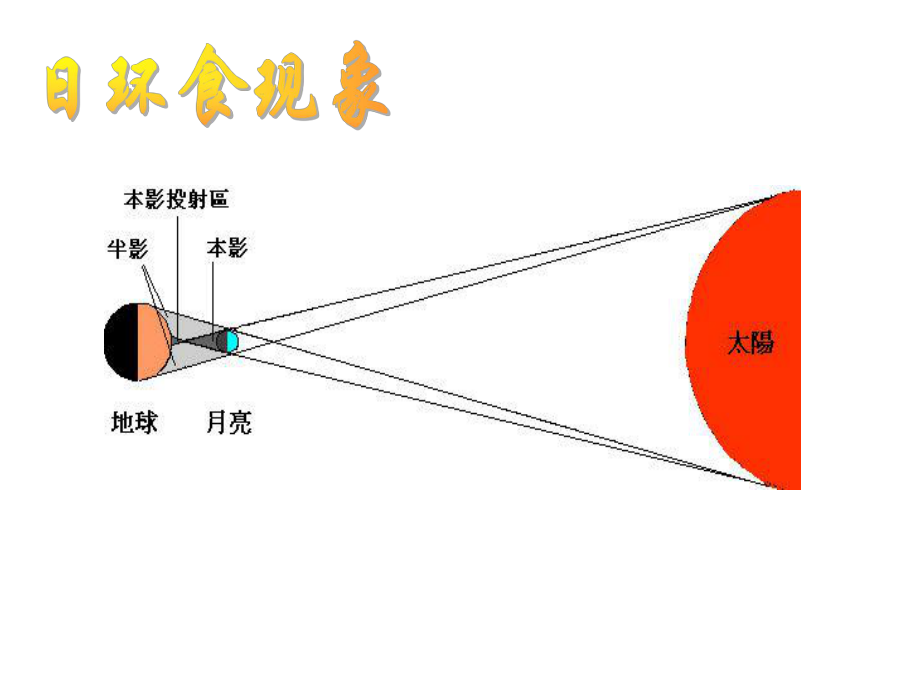
2、日环类比直线与圆的位置关系，想一想在日环食现象演示中两个圆有几种位置关系呢？食现象演示中两个圆有几种位置关系呢？利用手中两个圆，利用手中两个圆，两人一组分工合作两人一组分工合作，依，依据据“日环食日环食”的过程进行操作试验，把圆的过程进行操作试验，把圆形纸片由远到近沿着这两个圆的圆心所在形纸片由远到近沿着这两个圆的圆心所在直线表示的方向，找出这直线表示的方向，找出这两个圆可能形成两个圆可能形成的位置关系的位置关系 ，画在练习本上，画在练习本上，并说一说，并说一说你你是根据什么来分类的是根据什么来分类的. .OOOOO O O O O O O OO OOOOOO O O O O O O OO O

3、OOOOO O O O O O O OO OOOOOO O O O O O O OO O第一种情况第一种情况第二种情况第二种情况第三种情况第三种情况第第四种情况四种情况第第五种情况五种情况相离相离每一个圆上的点都在另每一个圆上的点都在另一个圆的一个圆的外部外部。叫做两圆叫做两圆外离外离特点：特点：两圆两圆没有没有公共点公共点，特点：特点：两圆两圆没有没有公共点，公共点，并且其中一个圆上并且其中一个圆上的所有点都在另一的所有点都在另一个圆的个圆的内部内部，叫做两圆叫做两圆内含内含相切相切特点：特点：两圆有两圆有唯一唯一个公共点，个公共点，并且除了这个切点以外，并且除了这个切点以外，每一个圆上的点

4、都在另每一个圆上的点都在另一个圆的一个圆的外部外部，叫做两圆叫做两圆外切外切。特点：特点： 两圆有两圆有唯一唯一的公共点，的公共点，除了这个点以外，一个除了这个点以外，一个圆上一的所有点在另一圆上一的所有点在另一个圆的个圆的内部内部，叫做两圆叫做两圆内切内切。相交相交两圆有两圆有两个两个公共点公共点特点：特点：叫做两圆叫做两圆相交相交猜想：猜想：直线和圆的位置关系可用直线和圆的位置关系可用d、r的代数表达的代数表达 式来表示，那么圆与圆的位置关系要用那式来表示，那么圆与圆的位置关系要用那 些量来表示？些量来表示？O1r1O2r2dO1r1O2r2dO1r1O2r2dO2r2dO1r1r1dO2

5、r2O1O1r1O2r2dO1r1O2r2dO1r1O2r2dO2r2dO1r1r1dO2r2O1两圆外离两圆外离两圆外切两圆外切两圆相交两圆相交两圆内切两圆内切两圆内含两圆内含观观察察与与思思考考怎样从两圆的圆心距与两圆半径的数量关怎样从两圆的圆心距与两圆半径的数量关系来判断两圆的位置关系系来判断两圆的位置关系?外离外离探讨两圆位置关系的代数表达式O1O2 r1 + r2 O1O2= r1 + r2 r1 -r2 O1O2r1 + r2 O1O2=r1 - r2 0O1O2r1+r2d=r1+r2r1- -r2 dr1+r2d= r1- -r2 0 d r1- -r2 公共点公共点圆心距和半

6、径的关系圆心距和半径的关系两圆位置两圆位置一圆在另一一圆在另一圆的外部圆的外部一圆在另一一圆在另一圆的外部圆的外部两圆相交两圆相交一圆在另一一圆在另一圆的内部圆的内部一圆在另一一圆在另一圆的内部圆的内部名称名称例例: :如图如图AA、BB、CC两两外切，两两外切，AB=5AB=5，BC=6BC=6 AC=7 AC=7求：求：AA、BB、CC的半径的半径解：解：ABC1、把自行车的两个轮子看作两个圆，则它们、把自行车的两个轮子看作两个圆，则它们的位置关系的位置关系_公共点公共点_个。个。外离外离02、两个同心圆的位置关系是：、两个同心圆的位置关系是：_内含内含3、圆、圆O1和圆和圆O2的半径分别

7、为的半径分别为R、r，圆心距为，圆心距为d在下列情况下圆在下列情况下圆O1和圆和圆O2的位置关系怎样？的位置关系怎样？(1)R=4 r=3 d=8外离外离(2)R=4 r=3 d=1内切内切(3)R=1 r=6 d=7外切外切(4)R=5 r=3 d=3相交相交(5)R=5 r=3 d=1内含内含4、两圆内切，其中一个圆的半径为、两圆内切，其中一个圆的半径为5，两圆的，两圆的 圆心距为圆心距为2，则另一个圆的半径为，则另一个圆的半径为_.3或或75、已知、已知 O1、 O2的半径为的半径为r1、r2，如果，如果r1 5，r23，且，且 O1、 O2相切，那么圆心距相切，那么圆心距 d=_.8或

8、或2如图如图OO的半径为的半径为5cm5cm，点，点P P是是OO外一点，外一点，OP=8cmOP=8cm。求：求：(1)(1)以以P P为圆心作为圆心作PP与与OO外切，小圆外切，小圆P P 的半径是多少的半径是多少? ? (2) (2)以以P P为圆心作为圆心作PP与与OO内切，大圆内切，大圆PP的半径是多少的半径是多少? ?解：解：(1)(1)设设OO与与PP外切外切 于点于点A A，则，则 PA=OP-OAPA=OP-OA PA=3 cm PA=3 cm(2)(2)设设OO与与PP内切内切 于点于点B B，则，则 PB=OP+OBPB=OP+OB PB=13 cm. PB=13 cm.0PAB.