演示文稿3 (2)

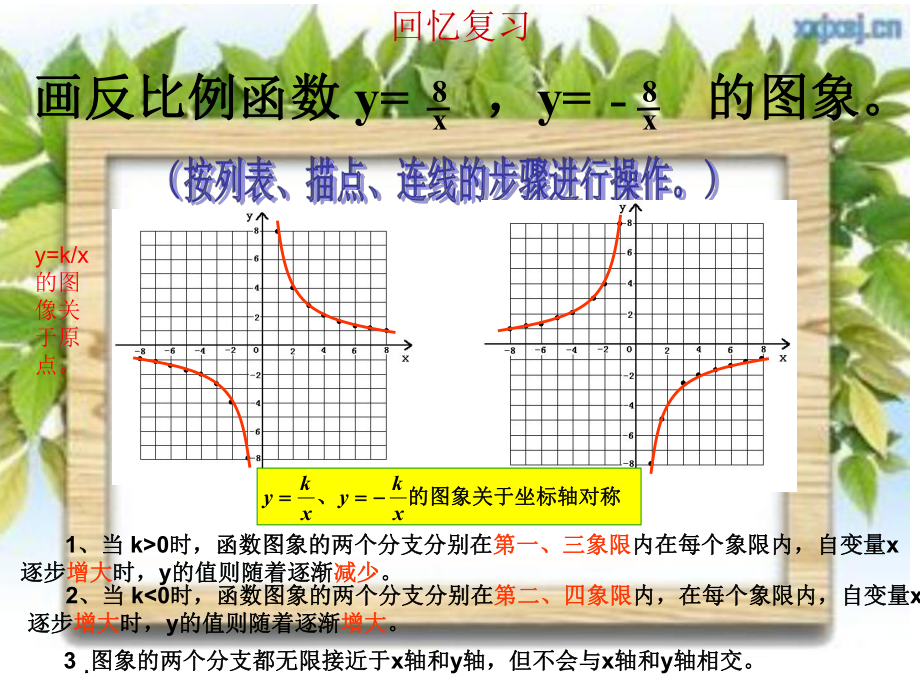
1、26.1.2 反比例函数的反比例函数的 图象和性质图象和性质(2)制作：段国建制作：段国建的的图图象象关关于于原原点点对对称称xky 回忆复习8x画反比例函数画反比例函数 y= ，y= 的图象。的图象。8x 1、当、当 k0时，函数图象的两个分支分别在时，函数图象的两个分支分别在第一、三象限第一、三象限内在每个象限内，自变量内在每个象限内，自变量x逐步逐步增大增大时，时，y的值则随着逐渐的值则随着逐渐减少减少。 2、当、当 k0时，函数图象的两个分支分别在时，函数图象的两个分支分别在第二、四象限第二、四象限内，在每个象限内，自变量内，在每个象限内，自变量x逐步逐步增大增大时，时，y的值则随着逐

2、渐的值则随着逐渐增大增大。3 ?图象的两个分支都无限接近于图象的两个分支都无限接近于x轴和轴和y轴，但不会与轴，但不会与x轴和轴和y轴相交。轴相交。的的图图象象关关于于坐坐标标轴轴对对称称、xkyxky y=k/x的图像关于原点。例例1:已知反比例函数的图象经过点已知反比例函数的图象经过点A(2，6).(1)这个函数的图象分布在哪些象限这个函数的图象分布在哪些象限?y随随x的增大如何的增大如何变化变化?(2)点点B(3，4)、C( ）和）和D（2，5）是否在）是否在这个函数的图象上？这个函数的图象上？142 , 452解解：（）设这个反比例函数为，：（）设这个反比例函数为，kyx图象过点图象过

3、点A（2，6）62k 解得：解得： 这个反比例函数的表达式为这个反比例函数的表达式为y=12/xk=120这个函数的图象在第一、第三象限，这个函数的图象在第一、第三象限，在每个象限内，随的增大而减小。在每个象限内，随的增大而减小。需要几个需要几个坐标点坐标点（）把点、和的坐标代入）把点、和的坐标代入y=12/x，可知点、，可知点、点的坐标满足函数关系式，点的坐标不满足函数关系式，点的坐标满足函数关系式，点的坐标不满足函数关系式，所以点、点在函数所以点、点在函数y=12/x12/x的图象上，点不在这个的图象上，点不在这个函数的图象上。函数的图象上。Xy=k 例2：反比例函数y=4/x的图像上有三

4、点（x1,y1),(x2,y2)(x3，y3)，其中 x1x200， 函数图象在第一、三象限 x1x20 x3， (x1，y1)，(x2，y2)在第三象限， (x3，y3)在第一象限 y10，y20. k0时，在每个象限内y随x的 增大而减小， y2y10. y2y10y3.方方法法一一方法二数形结合思想0yxx1y1x2y2x3y3 1，反比例函数的增减性不是连续的，因此在涉及反比例函数的增减性时，一般都是指在各自象限内的增减情况 2，反比例函数图象的位置和函数的增减性，都是由反比例系数 k 的符号决定的；反过来，由双曲线的位置和函数的增减性，也可以推断出 k 的符号 3，解决反比例函数的相

5、关问题时，往往我们需要画出函数的大致图象(即草图)采用数形结合的方法，解决问题更直观方法总结：k 的几何意义的几何意义 【例 3】 过如图 26-1-4 所示双曲线上任一点 P 作 x 轴、y轴的垂线 PM、PN，求四边形 PMON 的面积 1， 若 P 在第四象限，或双曲线在第一、三象限，则同样有 S 四边形PMON|k|. 2，因此 k 的几何意义为：过双曲线上任意一点作 x 轴、y 轴的垂线，所得的四边形的面积为|k|.3，所得三角形的面积为|k|2.【跟踪训练】 1图 26-1-2 是我们学过的反比例函数图象，它的函数解析式可能是( )Ayx2图 26-1-2B【跟踪训练】图象大致是(

6、 )B3、已知反比例函数、已知反比例函数 (1)若函数的图象位于第一三象限，若函数的图象位于第一三象限， 则则k_; (2)若在每一象限内，若在每一象限内，y随随x增大而增大，增大而增大， 则则k_.4kyxy2y3 B、y2y1y3C、y3y1y2 D、y3y2y1 (2)、考察函数考察函数 的图的图象象, ,当当x=-2x=-2时时,y=,y= _ _ , ,当当x-2x-2时时,y,y的取值范围是的取值范围是 _ _ ; ;当当y y-1-1时时,x,x的取值范围是的取值范围是 _ _ . .xy2B-1-1y0X0【跟踪训练】的图象交于点 M(a,1)，MNx 轴于点N(如图 26-1-6)，若OMN的面积等于 2，求这两个函数的解析式图 26-1-6【跟踪训练】为此图象上的一动点，过点 A 分别作 ABx 轴和 ACy 轴，垂足分别为 B，C，则四边形 OBAC 周长的最小值为( ）图 26-1-5A4B3C2D1解析：要使四边形的周长最小，则需要四边形为正方形，此时 OBABACOC1，所以周长为 4.A课后思考：1、已知，关于、已知，关于x的一次函数的一次函数 和和反比例函数反比例函数 的图象都经过点（的图象都经过点（1，-2）