计算机硬件技术基础 微型计算机原理与接口技术 第三次课微型计算机的算术运算基础

1、有符号数的机器数表示方法有符号数的机器数表示方法-原码、反码、补码原码、反码、补码1.2 微型计算机的算术运算基础微型计算机的算术运算基础三种机器码的最高位都是符号位，三种机器码的最高位都是符号位，0为正数，为正数，1为负数。为负数。1对于正数，三种编码都一样；对于负数对于正数，三种编码都一样；对于负数,三种三种编码互不相同。编码互不相同。2求真值：原码真值直接求取；反码和补码变换求真值：原码真值直接求取；反码和补码变换成相应的原码再进行求取。成相应的原码再进行求取。33.3.数的定点和浮点表示数的定点和浮点表示1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表

2、示方法计算机中数的表示方法 计算机中小数如何表示？小数点如何表示？定点表示浮点表示 根据根据小数点的位置是否固定小数点的位置是否固定，数的表示方法分为：，数的表示方法分为：定点数浮点数3.3.数的定点和浮点表示数的定点和浮点表示1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 总原则总原则 计算机中不用某个二进制位来表示小数点，而是计算机中不用某个二进制位来表示小数点，而是隐含规隐含规定小数点的位置定小数点的位置。定点数定点数 浮点数浮点数 根据小数点的位置是否固定，数的表示方法可分为根据小数点的位置是否固定，数的表示方法可分为定点定

3、点表示表示和和浮点表示浮点表示，相应的机器数就叫，相应的机器数就叫定点数定点数或或浮点数浮点数。对于任一个二进制数对于任一个二进制数X X，通常可表示成：通常可表示成：X = 2J S3.3.数的定点和浮点表示数的定点和浮点表示1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 阶码的底阶码的底阶码阶码尾数尾数说明说明尾数尾数S表示数表示数X的全部有效数字；的全部有效数字；阶码阶码J则指出了小数点的位置；则指出了小数点的位置；S值和值和J值均可正可负；值均可正可负；当当J固定时固定时,表示是定点数；当表示是定点数；当J值可变时，表示是浮

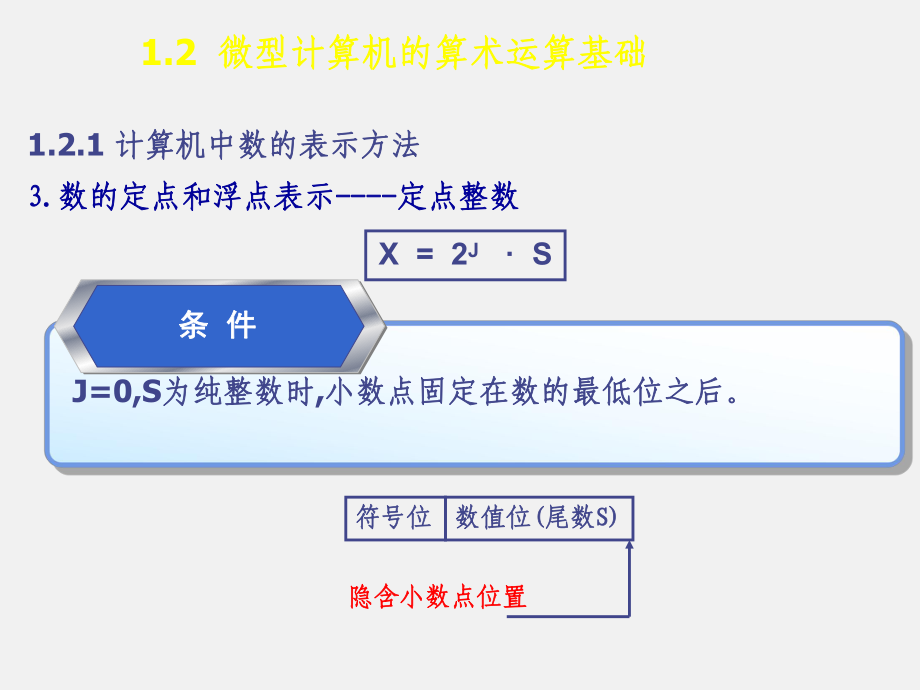
4、点数。值可变时，表示是浮点数。X = 2J S3.3.数的定点和浮点表示数的定点和浮点表示-定点整数定点整数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 符号位符号位数值位数值位( (尾数尾数S)S)隐含小数点位置隐含小数点位置条条 件件 J=0,S为纯整数时为纯整数时,小数点固定在数的最低位之后。小数点固定在数的最低位之后。X = 2J S3.3.数的定点和浮点表示数的定点和浮点表示-定点小数定点小数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 条条 件件 J=0,

5、S为纯小数时为纯小数时,小数点固定在数的最高位之前。小数点固定在数的最高位之前。符号位符号位数值位数值位( (尾数尾数S)S)隐含小数点位置隐含小数点位置定点整数和定点小数在计算机中表示形式没什么区别，定点整数和定点小数在计算机中表示形式没什么区别，其小数点完全靠事先的约定而隐含在不同位置。其小数点完全靠事先的约定而隐含在不同位置。3.3.数的定点和浮点表示数的定点和浮点表示1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 符号位符号位数值位数值位( (尾数尾数S)S)隐含小数点位置隐含小数点位置符号位符号位数值位数值位( (尾数尾数

6、S)S)隐含小数点位置隐含小数点位置3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 如何处理的既有整数部分又有小数部分的数据？尾数部分尾数部分阶符阶符Jf Jf 阶码阶码J J 数符数符Sf Sf 尾数尾数( (也叫有效数也叫有效数) )S S阶码部分阶码部分格式格式: :3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 十进制：十进制：-0.00223-0.

7、00223-0.223-0.2231010-2-2阶码一般用补码定点整数表示，尾数一般用补码或原码阶码一般用补码定点整数表示，尾数一般用补码或原码定点小数表示。定点小数表示。一般对尾数进行规格化处理，即保证尾数的最高位是一般对尾数进行规格化处理，即保证尾数的最高位是1,1,实际大小通过阶码来进行调整。实际大小通过阶码来进行调整。二进制：二进制：-0.00101-0.00101-1.01-1.012 2-3-33.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 尾数部分尾数部分阶符

8、阶符Jf Jf 阶码阶码J J 数符数符Sf Sf 尾数尾数( (也叫有效数也叫有效数) )S S阶码部分阶码部分格式格式: :十进制：十进制：-22.3-22.3-2.23-2.2310101 1二进制：二进制：-0.00101-0.00101-1.01-1.012 2-3-3是否可以通过某种方式使得阶码总为正，但又使得数值不失真？3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 阶码+整数(约定好)非负值存储存储存储形式的阶码- -整数(约定好) 真实值还原还原十进制：十进

9、制：-22.3-22.3-2.23-2.2310101 1二进制：二进制：-0.00101-0.00101-1.01-1.012 2-3-3IEEE754IEEE754标准：单精度标准：单精度(32(32位位) )、双精度、双精度(64(64位位) )、扩展精度、扩展精度(80(80位位) )313022 0符号位符号位阶码阶码有效数有效数1.1.636251 0符号位符号位阶码阶码有效数有效数1.1.单精度数双精度数3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 二进制：二

10、进制：-0.00101-0.00101-1.01-1.012 2-3-3797863 0符号位符号位阶码阶码1 有效数有效数. .扩展精度数浮点数如何比较大小？浮点数如何比较大小？阶码值大小的比较阶码值大小的比较 为了方便阶码值的比较，真阶码加上一个常数偏置值才是格式阶码，且使格式阶码恒为正数。3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 313022 0符号位符号位阶码阶码有效数有效数1.1.单精度数3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计

11、算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 1823+1+127调整值：调整值：优优 势：势：容易比较大小、简化形式容易比较大小、简化形式参数参数单精度单精度双精度双精度扩展精度扩展精度格式宽度格式宽度323264648080符号位数符号位数1 11 11 1有效数位数有效数位数23+123+152+152+16464阶码宽度阶码宽度8 811111515最大阶码值最大阶码值+127+127+1023+1023+16383+16383最小阶码值最小阶码值-126-126-1022-1022-16382-16382阶码偏置值阶码偏置值+127+

12、127+1023+1023+16383+16383IEEE浮点数格式的参数浮点数格式的参数值值3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 313022 0符号位符号位阶码阶码有效数有效数单精度数3.3.数的定点和浮点表示数的定点和浮点表示-浮点数浮点数1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 (-1)(-1)符号位符号位（1+0.1+0.有效数）有效数）( (阶码阶码-127)-127) 求出下面几个十进

13、制数的单精度的浮点数表求出下面几个十进制数的单精度的浮点数表示：示： 3，-2 ，1 ，-256.3753 = 11B = +1.121 Step1：将十进制数化为二进制的科学记数法Step2：真阶码+阶码偏置值=格式阶码，并化为二进制1 + 127 = +128 = 1000 0000Step3：确定符号位、阶码和有效数的二进制313022 01.01000 0000100 0000 0000 0000 0000 000040400000HStep4：转化为十六进制计算实例计算实例 求出下面几个十进制数的单精度的浮点数表求出下面几个十进制数的单精度的浮点数表示：示： 3，-2 ，1 ，-25

14、6.375-2= -10B = -1.021 Step1：将十进制数化为二进制的科学记数法Step2：真阶码+阶码偏置值=格式阶码，并化为二进制1 + 127 = +128 = 1000 0000Step3：确定符号位、阶码和有效数的二进制313022 01.11000 0000000 0000 0000 0000 0000 0000C0000000HStep4：转化为十六进制计算实例计算实例计算实例计算实例 求出单精度浮点数求出单精度浮点数E9BA8000H的真值。的真值。Step1：将十六进制化为二进制Step2：确定符号位，阶码值，有效数符号：符号：1（负）（负）Step3：计算真值E9

15、BA8000H=1,110 1001 1,011 1010 1000 0000 0000 0000B格式阶码值：格式阶码值：110 1001 1B=211，真阶码，真阶码 值值211-127 = 84有效数：有效数：(1+0.011 1010 1)B = 1.4921875-1.49218752841) 1) 二进制码二进制码2)2)BCDBCD码码3)3)ASCIIASCII码码三三种种表表示示方方法法 非压缩非压缩BCDBCD码码 压缩压缩BCDBCD码码一般在计算机的输入，输出设备中使用。一般在计算机的输入，输出设备中使用。在运算处理过程中使用在运算处理过程中使用4.4.无符号数的机器数

16、表示方法无符号数的机器数表示方法1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 BCDBCD码码 非压缩非压缩BCDBCD码码 压缩压缩BCDBCD码码4.4.无符号数的机器数表示方法无符号数的机器数表示方法1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.1 计算机中数的表示方法计算机中数的表示方法 每位每位BCD码用码用4位二进制表示，一位二进制表示，一个字节表示个字节表示2位位BCD码。码。每位每位BCD码用一个字节表示，高码用一个字节表示，高4位总是位总是0000，低，低4位表示位表示09。00001001 0

17、00000111001 001193十进制数BCD码十进制数BCD码000008 1000100019 100120010100001 000030011110001 000140100120001 001050101130001 001160110140001 010070111150001 0101 十进制与压缩十进制与压缩BCDBCD码对照表码对照表ASCIIASCII码（美国标准信息交换码）码（美国标准信息交换码）每位每位ASCII码用码用8位二进制表示位二进制表示,最高位为最高位为0,低七位组合表示低七位组合表示128种编码种编码1.2.2 1.2.2 计算机中有符号数的运算计算机中

18、有符号数的运算补补 码码 的的 加加 减减 法法 运运 算算 规规 则则1溢溢 出出 与与 溢溢 出出 判判 断断2补码的加减法运算公式：补码的加减法运算公式：1. 1. 补码的运算规则补码的运算规则XY补=X补+Y补-Y补的求法：先求-Y原，再求-Y补Y补连同符号位取反加11.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.2 计算机有符号数的运算计算机有符号数的运算补码加、减法运算规则补码加、减法运算规则: : 参加运算的数都用补码表示。参加运算的数都用补码表示。 数据的符号与数据一样参加运算。数据的符号与数据一样参加运算。 求差时将减数求补，用求和代替求差。求差时将减数求补，

19、用求和代替求差。 运算结果为补码。如果符号位为运算结果为补码。如果符号位为0 0，表明运算结果为正；，表明运算结果为正；如果符号位为如果符号位为1 1，则表明运算结果为负。，则表明运算结果为负。 符号位的进位为模值，应该丢掉。符号位的进位为模值，应该丢掉。1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.2 计算机有符号数的运算计算机有符号数的运算1. 补码的运算规则补码的运算规则XY补=X补+Y补例例1.3: X=36，Y=88，求求X+Y、X-Y。 X+Y补补=X补补+Y补补= 01111100X-Y补补=X补补+-Y补补= 11001100 X+Y= X+Y补补补补= 01

20、111100 =(+124)10 X-Y = X- Y补补补补= 10110100 =(-52)10练习练习解解: : X补补=00100100Y补补=01011000,-Y补补=10101000已知机器字长已知机器字长n n8 8位，位，x x120120， y y1010，求，求x xy y？【例题例题】x=+1111000，y1010【解解】：运算结果符号与被加数符号相反. 什么是溢出现象？如何判断？什么是溢出现象？如何判断？1.1. 补码的加减法运算规则补码的加减法运算规则 1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.2 计算机有符号数的运算计算机有符号数的运算小小

21、 结结负数的补码与对应正数的补码之间的转换可用同一方法负数的补码与对应正数的补码之间的转换可用同一方法求补运算实现，因而可简化硬件；求补运算实现，因而可简化硬件；可将减法变为加法运算，从而省去减法器；可将减法变为加法运算，从而省去减法器；有符号数和无符号数的加法运算可用同一加法器电路完有符号数和无符号数的加法运算可用同一加法器电路完成，结果都正确。成，结果都正确。 当结果超出补码表示的数值范围时，补码运算将会当结果超出补码表示的数值范围时，补码运算将会出错。这种现象称为出错。这种现象称为“溢出溢出”。2.2. 溢出与溢出判断溢出与溢出判断 1.2 微型计算机的算术运算基础微型计算机的算术运算基

22、础1.2.2 计算机有符号数的运算计算机有符号数的运算溢出？溢出？如何判断溢出？如何判断溢出？1 1，有溢出，有溢出0 0，无溢出，无溢出OF=C1OF=C1 C2=C2=2.2. 溢出与溢出判断溢出与溢出判断 1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.2 计算机有符号数的运算计算机有符号数的运算数值位f fb bn-1n-1b bn-2 n-2 b b1 1 b b0 0=1=1OFOFC C1 1C C2 2进位位C C最高数值位符号位C1与与C2相同，无溢出，否则有溢出相同，无溢出，否则有溢出因为因为C C2 2=1,C=1,C1 1=0,OF=C=0,OF=C1

23、1 C C2 2=1,=1,所以有溢出所以有溢出, ,结果不对。结果不对。 因为因为C C2 2=0,C=0,C1 1=0,OF=C=0,OF=C1 1 C C2 2=0,=0,所以无溢出所以无溢出, ,结果正确。结果正确。 例例: : 求求:55+66:55+66 55 55补补=00110111=00110111+ 66+ 66补补=01000010=0100001001111001=12101111001=121补补例：例： 求：求：(-93)+(-59)(-93)+(-59) -93 -93补补= 10100011= 10100011+ -59+ -59补补= 11000101= 11

24、0001011 101101000=+10401101000=+104补补0 01 1根据根据C C1 1、C C2 2值亦可判断有溢出时是正溢出还是负溢出：值亦可判断有溢出时是正溢出还是负溢出： C C2 2C C1 1=00=11=00=11时，无溢出；时，无溢出； C C2 2C C1 1=01=01时，为正溢出；时，为正溢出； C C2 2C C1 1=10=10时，为负溢出。时，为负溢出。1)1)二进制码二进制码2)2)BCDBCD码码3)3)ASCIIASCII码码无无符符号号数数三三种种表表示示方方法法一般在计算机的输入，输出设备中使用。一般在计算机的输入，输出设备中使用。在运算

25、处理过程中使用在运算处理过程中使用运算结果无需调整运算结果需要调整1.2 微型计算机的算术运算基础微型计算机的算术运算基础1.2.3 计算机无符号数的运算计算机无符号数的运算十进制数BCD码十进制数BCD码000008 1000100019 100120010100001 000030011110001 000140100120001 001050101130001 001160110140001 010070111150001 0101 十进制与十进制与BCDBCD码对照表码对照表 1000+ 01111111求求BCDBCD码的码的8+78+7 非法的非法的BCDBCD码码和15的BCD码

26、为0001 0101若两个一位若两个一位BCDBCD数相加结果大于数相加结果大于9(1001),9(1001),则应作则应作加加6(0110)6(0110)修正修正; ;加法修正规则加法修正规则 1000+ 01111111对对BCDBCD码的码的8+78+7进行修正进行修正 + 01100001 0101结果大于结果大于9 9，需调整，需调整加加6 6修正修正结果正确，为结果正确，为1515 1001+ 011110000求求BCDBCD码的码的9+79+7 非法的非法的BCDBCD码码和16的BCD码为0001 0110若两个若两个BCDBCD数相加结果在本位并不大于数相加结果在本位并不大

27、于9 9（10011001）, ,但产生了进位但产生了进位, , 也应在本位作加也应在本位作加6 6（01100110）修正。修正。加法修正规则加法修正规则 1001+ 011110000对对BCDBCD码的码的9+79+7进行修正进行修正 + 01100001 0110个位不大于个位不大于9 9，有进位，需调整，有进位，需调整加加6 6修正修正结果正确，为结果正确，为1515 0110 0011 0100 10010001 1010求求BCDBCD码的码的63-4963-49 非法的非法的BCDBCD码码差14的BCD码为0001 0100减法修正规则减法修正规则 两个两个BCDBCD数相减

28、，若出现本位差超过数相减，若出现本位差超过9 9，应在，应在本位作减本位作减6 6修正。修正。对对BCDBCD码的码的63-4963-49进行修正进行修正 01100001 0100个位结果大于个位结果大于9 9，需调整，需调整减减6 6修正修正结果正确，为结果正确，为1414 0110 0011 0100 10010001 1010对对BCDBCD码的码的82-2982-29进行修正进行修正 01100101 0011结果不大于结果不大于9 9，但向高位有借位，但向高位有借位减减6 6修正修正结果正确，为结果正确，为5353 1000 0010 0010 10010101 1001减法修正规

29、则减法修正规则 两个两个BCDBCD数相减，若不超过数相减，若不超过9 9但向高位有借位，则但向高位有借位，则说明必然是借了说明必然是借了1616，多借了，多借了6 6，应在本位作减，应在本位作减6 6修正。修正。课后作业：课后作业：P P3232 1.81.8；加：加：（1 1）、求）、求BCDBCD码码17+1917+19； （2 2）、求）、求BCDBCD码码72-3872-38 1在下面关于微处理器的叙述中，错误的是在下面关于微处理器的叙述中，错误的是( ) 。A、微处理器是用超大规模集成电路制成的具有运算和控制功能的芯片微处理器是用超大规模集成电路制成的具有运算和控制功能的芯片 B、

30、一台计算机的一台计算机的CPU含有含有1个或多个微处理器个或多个微处理器 C、寄存器由具有特殊用途的部分内存单元组成，是内存的一部分寄存器由具有特殊用途的部分内存单元组成，是内存的一部分 D、不同型号的不同型号的CPU可能具有不同的机器指令可能具有不同的机器指令 2运算器在执行两个用补码表示的整数加法时，判断其是否溢出的规则运算器在执行两个用补码表示的整数加法时，判断其是否溢出的规则为为( )。A、两个整数相加，若最高位（符号位）有进位，则一定发生溢出两个整数相加，若最高位（符号位）有进位，则一定发生溢出B、两个整数相加，若结果的符号位为两个整数相加，若结果的符号位为0，则一定发生溢出，则一定发生溢出 C、两个整数相加，若结果的符号位为两个整数相加，若结果的符号位为1，则一定发生溢出，则一定发生溢出 D、两个同号的整数相加，若结果的符号位与加数的符号位相反，则一定两个同号的整数相加，若结果的符号位与加数的符号位相反，则一定发生溢出发生溢出 3运算器的主要功能是运算器的主要功能是( )。 A、算术运算算术运算 B、逻辑运算逻辑运算 C、算术运算与逻辑运算算术运算与逻辑运算 D、函数运算函数运算4运算器由很多部件组成，其核心部分是运算器由很多部件组成，其核心