七年级数学多边形内角和与外角和

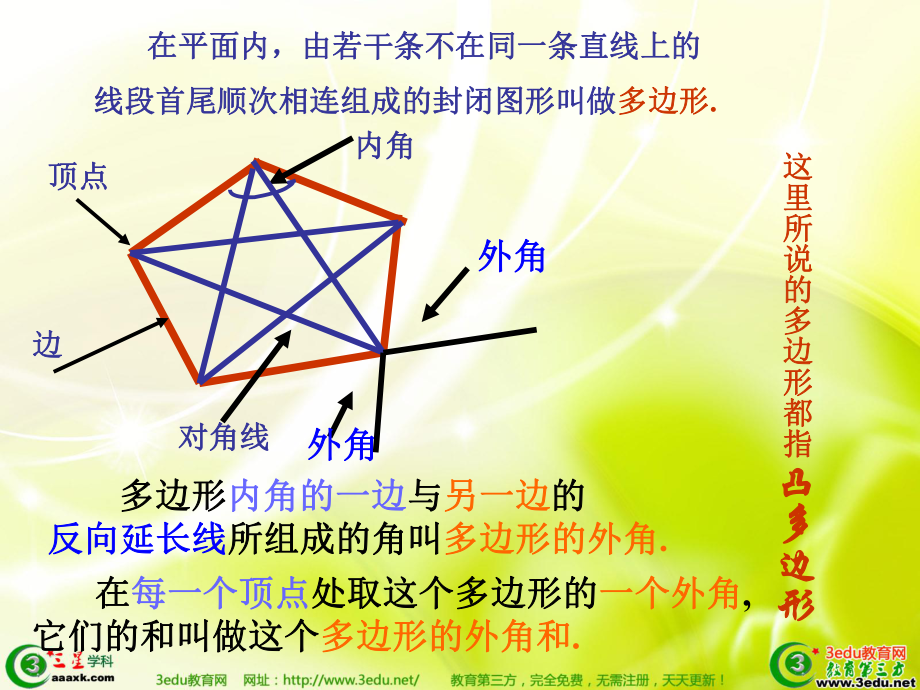
1、 顶点顶点边边内角内角 在平面内，由若干条不在同一条直线上的在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做线段首尾顺次相连组成的封闭图形叫做多边形多边形.顶点顶点内角内角边边对角线对角线这里所说的多边形都指这里所说的多边形都指凸多边形凸多边形外角外角外角外角 多边形多边形内角的一边内角的一边与与另一边另一边的的反向延长线反向延长线所组成的角叫所组成的角叫多边形的外角多边形的外角. 在在每一个顶点每一个顶点处取这个多边形的处取这个多边形的一个外角一个外角,它们的和叫做这个它们的和叫做这个多边形的外角和多边形的外角和. 画出多边形中从一个顶点出发的对角线，写出它的条数。画出

2、多边形中从一个顶点出发的对角线，写出它的条数。01235(2) 180n 多边形内角的一边与另一边的反向延长线所组成多边形内角的一边与另一边的反向延长线所组成的角叫做这个的角叫做这个多边形的外角(exterior angle) 在每个顶点处取这个多边形的一个外角，它们的和在每个顶点处取这个多边形的一个外角，它们的和叫做这个叫做这个多边形的外角和. 一般地，一般地，在多边形的任一顶点处在多边形的任一顶点处按顺按顺( (逆逆) )时针方向可作外角，时针方向可作外角，n n边形有边形有n n个外角个外角. . 54321新知新知:探究探究在在n边形的每个顶点处各取一个外角，边形的每个顶点处各取一个外

3、角，这些外角的和叫做这些外角的和叫做n边形的外角和边形的外角和n边形外角和边形外角和=结论：结论：n n边形的外角和等于边形的外角和等于360360-(n-2) 180=360 A1E BCD 2 3 4 5F nn n个平角个平角-n-n边形内角和边形内角和=n180 你能写出每个图形中对角线的总条数吗？如果不行，请画出所你能写出每个图形中对角线的总条数吗？如果不行，请画出所有对角线。有对角线。0259 太难画了，能不全画出太难画了，能不全画出对角线而计算出来吗？对角线而计算出来吗？ 你能告诉我二十边你能告诉我二十边形的对角线条数吗？形的对角线条数吗？五十边形呢？一百边五十边形呢？一百边形呢

4、？形呢？n n边形呢？边形呢？20归纳总结归纳总结边数边数34568n从一个顶点出发从一个顶点出发的对角线的条数的对角线的条数上述对角线分成上述对角线分成的三角形个数的三角形个数总的对角线条数总的对角线条数0101222353495620n-3n-2n(n-3)2 过某个多边形一个顶点的所有对角线过某个多边形一个顶点的所有对角线, 将这个多边形分成将这个多边形分成5个三角形个三角形.这个多边形这个多边形 是几边形是几边形?它的内角和是多少它的内角和是多少?例例1.解解:依题意依题意, 这个多边形是七边形这个多边形是七边形,它的内角和是它的内角和是(72) 180=900例例2. 如果一个多边形

5、的内角和是如果一个多边形的内角和是1440， 那么这是那么这是 边形。边形。十十 解：由解：由n边形的内角和公式可得边形的内角和公式可得（n 2） 180 = 1440 n 2 = 8 n = 10这是十边形。这是十边形。 方法小结：方法小结： 求多边形的边数、求多边形的边数、角度的常用方法角度的常用方法: 利用公式列方程利用公式列方程.例例3：6、若正、若正n边形的一个内角是边形的一个内角是144，那么，那么n= .解：由解：由n边形的内角和公式可得：边形的内角和公式可得：(n 2) 180 = 144n180n 360 = 144n180n 144n=36036n = 360n = 101

6、0例4一个多边形的内角和等于它的外一个多边形的内角和等于它的外角和的角和的3 3倍，它是几边形？倍，它是几边形？ 解：设这个多边形是解：设这个多边形是n n边形，则它的内角和边形，则它的内角和是是( (n n2)2)180180, ,外角和等于外角和等于360360，所以：所以：( (n n2)2)180=3180=3360360解得：解得：n n=8=8答答: :这个多边形是八边形这个多边形是八边形. . 课堂练习课堂练习:1.1.一个多边形的外角都等于一个多边形的外角都等于6060，这个多边形是，这个多边形是n n边形？边形？ 解：因为多边形的外角和等于360，所以根据题意，可知道这个多边

7、形的边数是：36060=6 .答:这个多边形是六边形. 2.2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分，这种多边形是几边形？为什么？图形的一部分，这种多边形是几边形？为什么？ 解：设：这个正多边形的一个内角为解：设：这个正多边形的一个内角为x x，则由题图得：则由题图得：3 3x x=360=360. . x x=120=120. .再根据多边形的内角和公式得：再根据多边形的内角和公式得：n n120120=(=(n n2)2)180180. . 解得解得n n=6 . =6 . 答答: :( (略略) ) 学以致用学以致用

8、3、多边形内角和为、多边形内角和为1080则它是（则它是（ ）边形）边形。 2 2、十边形的内角和是（十边形的内角和是（ ） ; ; 如果十边形的如果十边形的各个内角都相等，那么它的一个内角是（各个内角都相等，那么它的一个内角是（ ） 4、多边形内角和为、多边形内角和为1800则它是（则它是（ ）边形。）边形。1、七边形内角和为（、七边形内角和为（ ）900 1440 十二十二 八八 144 求下列图形中求下列图形中x的值：的值：01400 x0 x(1)0 x0150012002X(2)0 x0120080075(3)C0 x0135ABDE0150060(4)ABCD课堂练习课堂练习 1、

9、十二边形的内角和是_； 2、若一个多边形的内角和是1620，则此多边形的 边数是_. 3、多边形的边数每增加一条，多边形内角和增加 _ 4、下列哪一个度数可成为某个多边形的内角和 ( ) A. 240 B.600 C. 1980 D. 2180 巩固练习巩固练习1 1、如果一个多边形的每一个外角等于、如果一个多边形的每一个外角等于3030, ,则这个多边形的边数是则这个多边形的边数是_。12n30=360n=12n边形外角和边形外角和=360 2 2、正五边形的每一个外角等于、正五边形的每一个外角等于_，每一，每一个内角等于个内角等于_。5X=360X=7272144解：设正五边形的每一个外角度数为解：设正五边形的每一个外角度数为x，由，由多边形的外角和等于多边形的外角和等于360度可得：度可得：所以每一个内角度数为所以每一个内角度数为108 3 3、已知一个多边形，它的内角和等于外角、已知一个多边形，它的内角和等于外角和的和的2 2倍，求这个多边形的边数。倍，求这个多边形的边数。 解：解： 设多边形的边数为设多边形的边数为n n 它的内角和等于它的内角和等于 (n-2)(n-2)180180， 多边形外角和等于多边形外角和等于360360， (n-2)(n-2)180180=2=2 360 360。 解得解得: n=6: