材料力学 第十四章 静不定问题分析

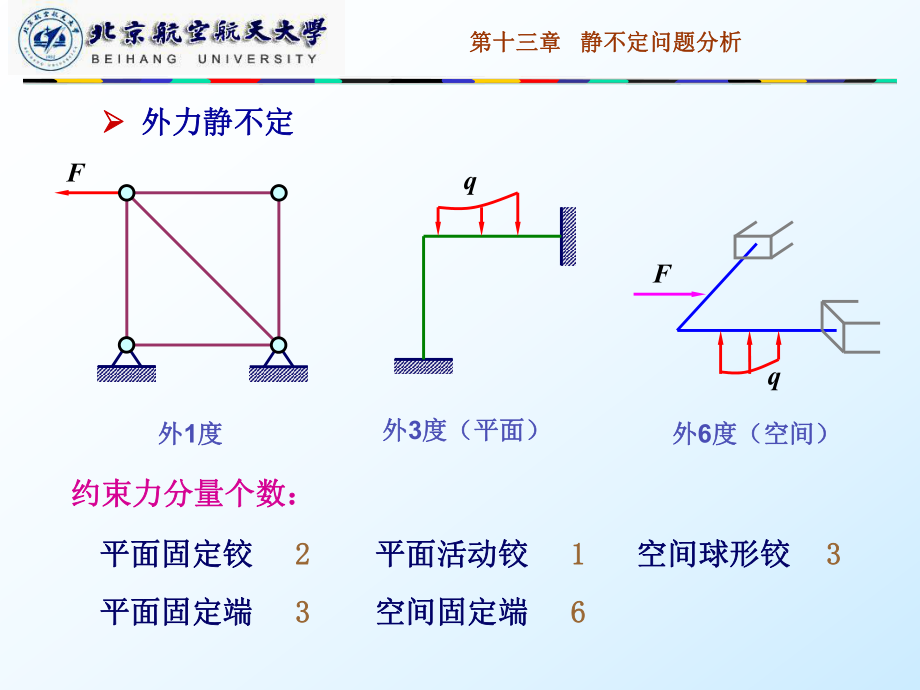
1、第十三章第十三章 静不定问题分析静不定问题分析第十三章第十三章 静不定问题分析静不定问题分析外力静不定结构外力静不定结构内力静不定结构内力静不定结构混合型静不定结构混合型静不定结构ABqABqAxFAyFBxFByFABqAxFAyFBxFByF第十三章第十三章 静不定问题分析静不定问题分析 外力静不定外力静不定外外1度度外外3度（平面）度（平面）外外6度（空间）度（空间）约束力分量个数：约束力分量个数：平面固定铰平面固定铰平面固定端平面固定端平面活动铰平面活动铰空间球形铰空间球形铰空间固定端空间固定端2 21 13 33 36 6FFqq第十三章第十三章 静不定问题分析静不定问题分析 内力静

2、不定内力静不定 (桁架桁架)内内1度度内内2度度静不定度静不定度 = m - ( 2n 3 ) m : 杆数；杆数；n ：节点数节点数FF第十三章第十三章 静不定问题分析静不定问题分析内内6度度（外（外3自由度）自由度）单闭口的平面单闭口的平面刚架或曲杆，刚架或曲杆，3度内静不定度内静不定FFq内内3度度SFNFMq 内力静不定内力静不定 (刚架刚架)第十三章第十三章 静不定问题分析静不定问题分析FF6度内力静不定度内力静不定, ,外外3自由度自由度FF5度内力静不定度内力静不定, ,加一中间铰减加一中间铰减少一度静不定少一度静不定FF4度内力静不定度内力静不定, ,加一根二力杆增加一加一根二

3、力杆增加一度静不定度静不定第十三章第十三章 静不定问题分析静不定问题分析 混合静不定混合静不定1（内）（内）1（外）（外） 2 度度3（内）（内）3（外）（外） 6 度度圆环在水平方向有一自由度圆环在水平方向有一自由度梁：外梁：外3环：内环：内3梁环接触：梁环接触：13+3+1=7 度度F圆环圆环FF第十三章第十三章 静不定问题分析静不定问题分析(a)(b)(c)(a): 内内2度度(b): 1度度(c): 2度度 混合静不定混合静不定（梁杆结构）（梁杆结构）第十三章第十三章 静不定问题分析静不定问题分析 几个概念：几个概念： 基本系统：基本系统：解除多余约束后的静定结构（静定基）解除多余约束

4、后的静定结构（静定基） 相当相当系统：系统：作用有载荷和多余反力的基本系统。作用有载荷和多余反力的基本系统。基本系统和相当系统不唯一基本系统和相当系统不唯一 分析要点：分析要点：1、 去除多余约束，建立相当系统去除多余约束，建立相当系统2、 建立补充方程（找变形协调条件）建立补充方程（找变形协调条件）3、 确定多余未知力确定多余未知力(多余内力和多余外力多余内力和多余外力)第十三章第十三章 静不定问题分析静不定问题分析一、一、 外力静不定结构分析外力静不定结构分析解除多余的外部约束，代之以支反力解除多余的外部约束，代之以支反力相当系统相当系统在解除约束处，建立变形协调条件在解除约束处，建立变形

5、协调条件建立补充方程建立补充方程ABCllABRCllHC00CCf ABCllRCM00AAf 第十三章第十三章 静不定问题分析静不定问题分析二、二、 内力静不定结构分析内力静不定结构分析切开提供多余内部约束的杆件，代之以截面上的内力切开提供多余内部约束的杆件，代之以截面上的内力相当系统相当系统利用切开截面的相对广义位移为零，建立变形协调条件利用切开截面的相对广义位移为零，建立变形协调条件建立补充方程建立补充方程mm/000m mm mm mf 第十三章第十三章 静不定问题分析静不定问题分析例：例：已知外力偶已知外力偶 M0 ，求，求B端约束端约束反力反力FB和水平位移和水平位移 。BH O

6、RAB1(b) B01cos1cosMF RMMR 解解：（1）求支反力）求支反力弯矩弯矩变形协调条件变形协调条件=0 BV 单位载荷法单位载荷法 BVB0032B011cos1cosd1302F RMRREIF RM REI 0B23MFR ORABM0FB(a)第十三章第十三章 静不定问题分析静不定问题分析(2)求求BH 讨论：选取哪种讨论：选取哪种单位载荷系统单位载荷系统? ORABM0FB(a)1 ORABFB(d) ORAB1(c)第十三章第十三章 静不定问题分析静不定问题分析B端的水平位移为端的水平位移为 BH002002012cos1sind3sinsin2d323MRREIM

7、RREIM REI 方法1 ORAB1(c) sinMR 00021cos312cos3MMRMRM 第十三章第十三章 静不定问题分析静不定问题分析B43F 方法2解静不定问题，求单位载荷系统的解静不定问题，求单位载荷系统的BF BH00220002012cos141cossind3324coscos2d3923MRRREIM RM REIEIM REI 1 ORABFB(d) 00012cos21cos33MMRMMR B41cossin1cossin3MF RRRR 第十三章第十三章 静不定问题分析静不定问题分析思考：思考：计算计算 ，下图相当系统选取是否正确？，下图相当系统选取是否正确？

8、BH oAB0MR03MR03MR对应的单位载荷系统：对应的单位载荷系统：oAB1R第十三章第十三章 静不定问题分析静不定问题分析例：例：求求B 端反力端反力qlABl相当系统相当系统qABBxFByF变形协调条件：变形协调条件：0,0BBf 单位载荷系统单位载荷系统 1 1AB单位载荷系统单位载荷系统 2 1AB第十三章第十三章 静不定问题分析静不定问题分析例：例：图示图示桁桁架，各杆架，各杆EA相同，求各杆轴力相同，求各杆轴力。a12345678aaP解：解：判断静不定度：判断静不定度：外力静定外力静定内力静不定度：内力静不定度： 8 - 2 5 + 3 = 11、 去除多余约束，建立相当

9、系统去除多余约束，建立相当系统2、 建立补充方程建立补充方程(找变形协调条件找变形协调条件)/0m m 1234568PN7N7mm第十三章第十三章 静不定问题分析静不定问题分析1234568111234568PN7N7 利用单位载荷法建立补充方程利用单位载荷法建立补充方程 N7PNi1817a6a5a4a30a201Nili2a2a2a72NP 2P 722NP 722N 722N 722NP 22 22 22 22 第十三章第十三章 静不定问题分析静不定问题分析8/17(22)(22) 0ii im miN N lEAaNPEA 722NP a12345678aaP12345681思考：若

10、求加载点的水平位移，如何选择单位载荷状态思考：若求加载点的水平位移，如何选择单位载荷状态12345681第十三章第十三章 静不定问题分析静不定问题分析思考：思考：求求BD杆的转角，正确杆的转角，正确的单位载荷系统是的单位载荷系统是_答：答：C、D1a1aADBC A B1a1aADBC C22aADBC22a D22aADBC22a第十三章第十三章 静不定问题分析静不定问题分析 基本概念基本概念 对称结构：对称结构：形状、截面尺寸、材料、支持形状、截面尺寸、材料、支持方式沿对称面对称。方式沿对称面对称。PM对称载荷对称载荷反对称载荷反对称载荷PFFPMMPPFFMM第十三章第十三章 静不定问题

11、分析静不定问题分析l利用对称变形条件利用对称变形条件可以唯一确定对称内力可以唯一确定对称内力0,0,CC N,.CCFM变形特征：变形特征：ABaFCFa内力特征：内力特征：ABaFCFaC C 0 , 0 , C 0 0CMCMNCFNCFF SC 0 0l利用对称性，可直接确定某（些）多余未知力，简化计算，利用对称性，可直接确定某（些）多余未知力，简化计算， 但并不降低静不定度。但并不降低静不定度。 对称问题的内力与变形特点对称问题的内力与变形特点第十三章第十三章 静不定问题分析静不定问题分析l利用反对称变形条件利用反对称变形条件 f C = 0 ，可以唯一确定反对称内力，可以唯一确定反对

12、称内力FSCl在结构对称点在结构对称点C，对称加载情形，可直接确定一个内力，对称加载情形，可直接确定一个内力，l 反对称加载情形，可直接确定两个内力。反对称加载情形，可直接确定两个内力。变形特征：变形特征：ABMCM内力特征：内力特征：ABMCMSCFSCFF NC 0 , 0 , MC = 0 f C 0 0C 反对称问题的内力与变形特点反对称问题的内力与变形特点第十三章第十三章 静不定问题分析静不定问题分析例：例：已知圆环已知圆环EI，求，求B、D相对位移相对位移d dABCDRFFoABAM2F0A RFCABAM2F0A 解解：（：（1）利用对称性，选取相当系统利用对称性，选取相当系统

13、RFCABAMNAFNAFAMN12AFF 0A C 第十三章第十三章 静不定问题分析静不定问题分析 sin2BFMMR 1M 201sin02BBFMRRdEI 1022BRMFREI 1sin,2BFRMMFR 解解：（2）利用单位载荷法，计算利用单位载荷法，计算MBBMoAB2F 1oAB 第十三章第十三章 静不定问题分析静不定问题分析 20232033441sin220.1494B DMMRdEIFRdEIFRFREIEI （3）计算计算B D ABCDRFF （i）利用整圆环）利用整圆环 1sin2MFR 1sin2MR ABCDR1 1第十三章第十三章 静不定问题分析静不定问题分析

14、（3）计算计算B D 20332221sinsin280.1494B DBRFRRdEIFRFREIEI 讨论：求讨论：求 ，哪种方法简单？，哪种方法简单？A C 1sin2MFR sinMR 1oABR （ii）利用）利用 圆环圆环14BMoAB2FR 第十三章第十三章 静不定问题分析静不定问题分析FABR2FRFABR2FR2F2F2F2F变形特征变形特征0,0,ANAMF0/A B内力特征内力特征SF未知力未知力反对称轴反对称轴AB例：例：小曲率圆环，已知小曲率圆环，已知R,EI.求求A截面内力截面内力.2F2FFRFSFSAB第十三章第十三章 静不定问题分析静不定问题分析1( )( )

15、001133(2) 0222SSMMRdA BEIF RFREIFF 1( )sin(1 cos )2( )sinSMF RFRMR AB112F2FFRFSFSAB第十三章第十三章 静不定问题分析静不定问题分析一类双反对称轴问题可仅用平衡条件求解一类双反对称轴问题可仅用平衡条件求解FFFF2a2a2a2a例：例：对称还是反对称问题？对称还是反对称问题？FFFSFS22cos45022SSFFFF 双反对称轴问题双反对称轴问题双对称轴问题双对称轴问题第十三章第十三章 静不定问题分析静不定问题分析 结构对称、载荷不对称的问题结构对称、载荷不对称的问题F结论结论: 结构对称、载荷不对称的平面结构问

16、题可结构对称、载荷不对称的平面结构问题可 分解为一个对称与一个反对称问题。分解为一个对称与一个反对称问题。2F2F2F2F第十三章第十三章 静不定问题分析静不定问题分析 中心对称问题中心对称问题DCABEFOmmm关于原点关于原点O中心对称中心对称oMCCmMA33MMmAC MCMAm30第十三章第十三章 静不定问题分析静不定问题分析FFFFDCABO123例：例：正方形行架杆，各杆正方形行架杆，各杆EI,O点固结。点固结。（1）几度静不定？）几度静不定？（2）求各杆内力。）求各杆内力。解：解： （1）4度静不定度静不定（2）中心对称中心对称各杆应变相同，各杆应变相同，FN 相同相同NNN2

17、cos45( 2 1)12FFFFFF FNFNFNF第十三章第十三章 静不定问题分析静不定问题分析112211211(),()2441(),()2FMxxMxF aF xMxxMxa EIFaEIFadxFaxFaEIdxFxEIaaCH12)16181481()8181(1211332220210改错改错 ： 求求C点支反力与铅垂位移点支反力与铅垂位移cva2a2aFC2FNFFFN4111x2x第十三章第十三章 静不定问题分析静不定问题分析2F2aa11x2x221122112121)(,)(4141)(,21)(xaxMxxMFxFaxMFxxM222112200311()2816aa

18、CVFFx dxaxdxEIEIFaEI 第十三章第十三章 静不定问题分析静不定问题分析例：例：右图问题是对称问题右图问题是对称问题还是反对称问题？还是反对称问题？对称问题对称问题FF反对称问题反对称问题2F2F第十三章第十三章 静不定问题分析静不定问题分析FFxFyFyFx F 2F2F2F2F第十三章第十三章 静不定问题分析静不定问题分析（a）面内加载）面内加载（b）面外加载）面外加载平面刚架平面刚架-轴线位于同一平面的刚架轴线位于同一平面的刚架面内加载面内加载-外载荷位于刚架轴线平面内（已研究）外载荷位于刚架轴线平面内（已研究）面外加载面外加载-外载荷位于垂直于刚架轴线平面外载荷位于垂直

19、于刚架轴线平面FCBADqMFCBADqM第十三章第十三章 静不定问题分析静不定问题分析 内力内力轴线平面内的内力分量（轴力轴线平面内的内力分量（轴力FN、面内面内 剪力剪力 FSz与面内弯矩与面内弯矩My）忽略不计）忽略不计 反力反力作用在轴线平面内的支反力与支反力偶矩作用在轴线平面内的支反力与支反力偶矩 忽略不计忽略不计 位移位移小变形时小变形时,横截面形心横截面形心在在轴线平面轴线平面内的位内的位 移移（轴线的面内变形轴线的面内变形）忽略不计忽略不计CBADFqMeECBDCBAMeSyFTNFyMSzFzMxyzCBAMeSyFTyMzMxyz第十三章第十三章 静不定问题分析静不定问题

20、分析结论：作用于平面结构的载荷总可分解为面内与面外结论：作用于平面结构的载荷总可分解为面内与面外载荷，分别引起面内与面外内力，可以解耦计算。载荷，分别引起面内与面外内力，可以解耦计算。面内内力与面内面内内力与面内约束力分量约束力分量*zF*xF*yMyMNFSF面外内力与面外面外内力与面外约束力分量约束力分量*zM*xMyFSyFxMT一般载荷的分解一般载荷的分解MF第十三章第十三章 静不定问题分析静不定问题分析讨论：对比面外与面内载荷的对称问题讨论：对比面外与面内载荷的对称问题面内受力：面内受力：NS0,0,0CzCCxFMF 面外受力特征：面外受力特征：S0,0CzCFT变形特征：变形特征

21、：0Cx 2a2aaFCBAzyxoa2aC2FCxM 面外载荷的对称问题面外载荷的对称问题第十三章第十三章 静不定问题分析静不定问题分析例：例：已知已知EI，GIP，求，求C点内力点内力 MCx 及铅垂位移及铅垂位移分析：分析：待求未知量待求未知量MCx变形条件：变形条件： Cx = 02a2aaFCBAzyxoa2aC2FCxM第十三章第十三章 静不定问题分析静不定问题分析1).求求MCXa2aCMCX1x2x2F1211()()() ()011122200(4)8(2)aaM xM x dxT xT xdxCXEIGIpGIEI FapMCXGIEIp 1()112M xMFxCX1()

22、222M xFx1()24T xMFaCX 11M x 02M x () 12T x 第十三章第十三章 静不定问题分析静不定问题分析a2aCMCX1x2x2F12).求铅垂位移求铅垂位移CV 211111112()()1112222242000113123()()82168aaaMFxx dxFxdxMFaadxCxCxCVEIEIGIpMaFaCxEIGIEIGIpp1()112M xMFxCx 1()222M xFx 1()24T xMFaCx 11M xx 22M xx ()22aT x 第十三章第十三章 静不定问题分析静不定问题分析 面外载荷的反对称问题面外载荷的反对称问题讨论：讨论：对比面外与面内载荷的对称问题对比面外与面内载荷的对称问题面内受力：面内受力：NS0,0,0CzCCxFMF 面内受力特征：面内受力特征：0CxM 变形特征：变形特征：2a2aaM0CBAzyxoa2aCzF012MCT Cz = 0, Cy 0 0第十三章第十三章 静不定问题分析静不定问题分析例：例：求图示结