中考数学中的二次函数的线段和差以及最值问题

1、二次函数与线段和差问题例题精讲：如图抛物线y=ax2+bx+c(a0与x轴交于A,B1,0，与y轴交于点C,直线y=12x-2经过点A,C.抛物线的顶点为D，对称轴为直线l,（1） 求抛物线解析式。（2） 求顶点D的坐标与对称轴l.（3） 设点E为x轴上一点，且AE=CE,求点E的坐标。（4） 设点G是y轴上的一点，是否存在点G，使得GD+GB的值最小，假设存在，求出G点坐标，假设不存在，说明理由。（5） 在直线l上是否存在一点F，使得BCF的周长最小，假设存在，求出点F的坐标及BCF周长的最小值，假设不存在，说明理由。（6） 在y轴上是否存在一点S,使得SD-SB的值最大，假设存在，求出S点

2、坐标，假设不存在，说明理由。（7） 假设点H是抛物线上位于AC上方的一点，过点H作y轴的平行线，交AC于点K，设点H的横坐标为h,线段HK=d求d关于h的函数关系式求d的最大值及此时H点的坐标（8） 设点P是直线AC上方抛物线上一点，当P点与直线AC距离最大值时，求P点的坐标，并求出最大距离是多少？1.如图，矩形的边OA在轴上，边OC在轴上，点的坐标为(10,8)，沿直线OD折叠矩形，使点正好落在上的处，E点坐标为(6,8)，抛物线经过、三点。1求此抛物线的解析式。2求AD的长。3点P是抛物线对称轴上的一动点，当PAD的周长最小时，求点P的坐标。2.如图，在平面直角坐标系中，抛物线与轴相交于点

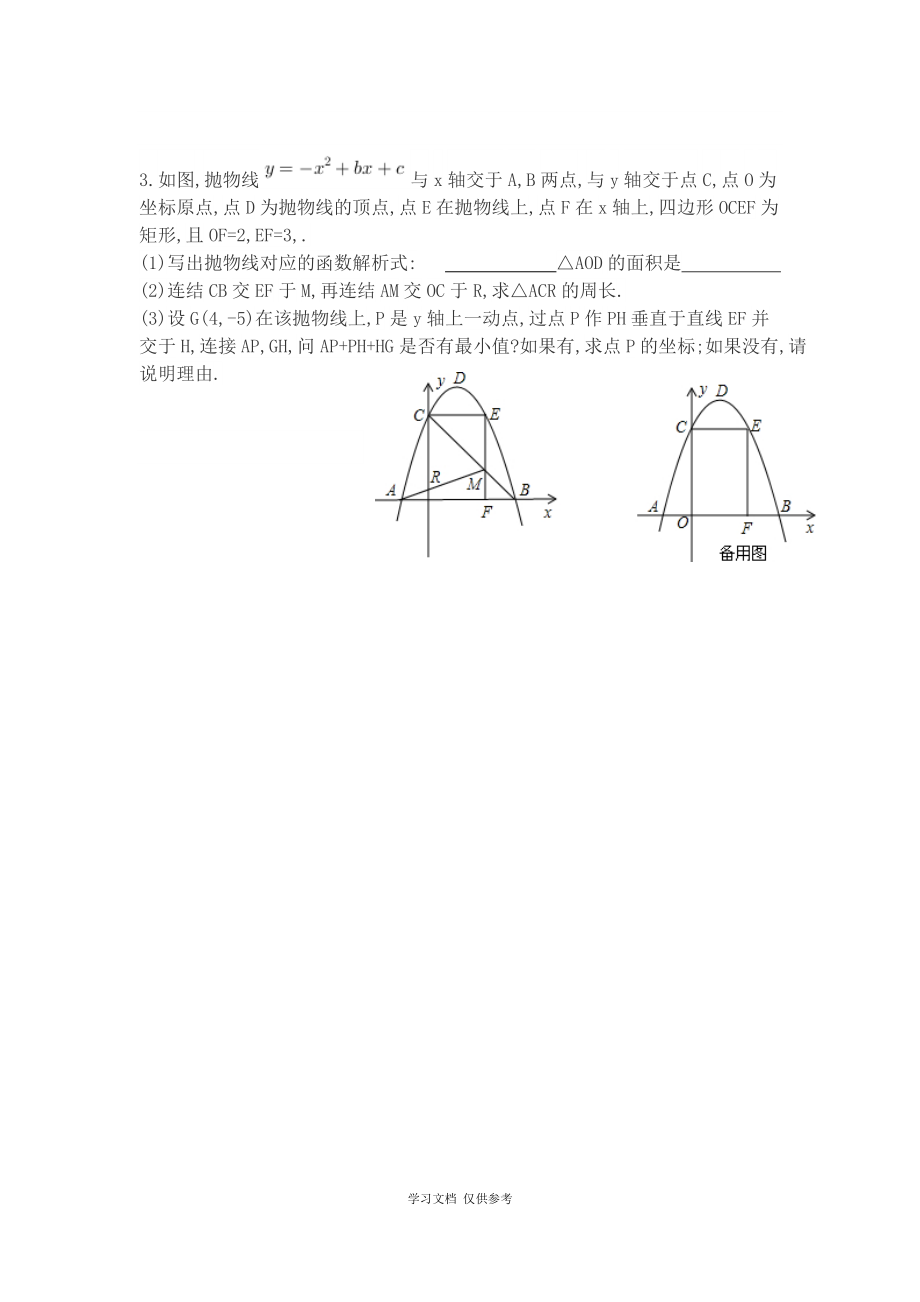
3、A，点B与点O关于点A对称。1填空：点B的坐标是  。2过点的直线其中与轴相交于点C，过点C作直线平行于轴，P是直线上一点，且PB=PC，求线段PB的长用含k 的式子表示，并判断点P是否在抛物线上，说明理由。3在2的条件下，假设点C关于直线BP的对称点恰好落在该抛物线的对称轴上，求此时点P的坐标。3.如图,抛物线与x轴交于A,B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,.(1)写出抛物线对应的函数解析式: AOD的面积是 (2)连结CB交EF于M,再连结AM交OC于R,求ACR的周长.(3)设G

4、(4,-5)在该抛物线上,P是y轴上一动点,过点P作PH垂直于直线EF并交于H,连接AP,GH,问AP+PH+HG是否有最小值?如果有,求点P的坐标;如果没有,请说明理由.4.在平面直角坐标系中，矩形的顶点O在坐标原点，顶点A、B分别在轴、轴的正半轴上，D为边OB的中点 假设、为边上的两个动点，且，当四边形的周长最小时，求点、的坐标yBODCAx5.四边形ABCD是直角梯形，BCAD，BAD=90°，BC与y轴相交于点M，且M是BC的中点，A、B、D三点的坐标分别是A，B，D3，0连接DM，并把线段DM沿DA方向平移到ON假设抛物线经过点D、M、N1求抛物线的解析式；2抛物线上是否存

5、在点P，使得PA=PC，假设存在，求出点P的坐标；假设不存在，请说明理由；3设抛物线与x轴的另一个交点为E，点Q是抛物线的对称轴上的一个动点，当点Q在什么位置时有|QE-QC|最大？并求出最大值6.已知，如图，二次函数图象的顶点为H，与x轴交于A、B两点B在A点右侧，点H、B关于直线对称1求A、B两点坐标，并证明点A在直线上；2求二次函数解析式；3过点B作直线BKAH交直线于K点，M、N分别为直线AH和直线上的两个动点，连接HN、NM、MK，求HN+NM+MK和的最小值 7.如图，已知点A(-4，8)和点B(2，n)在抛物线上1求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ

6、+QB最短，求出点Q的坐标；2平移抛物线，记平移后点A的对应点为A，点B的对应点为B，点C(-2，0)和点D(-4，0)是x轴上的两个定点当抛物线向左平移到某个位置时，AC+CB 最短，求此时抛物线的函数解析式；当抛物线向左或向右平移时，是否存在某个位置，使四边形ABCD的周长最短？假设存在，求出此时抛物线的函数解析式；假设不存在，请说明理由4x22A8-2O-2-4y6BCD-448.如图，在平面直角坐标系中，点A在抛物线y=x2+4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为1，11求线段AB的长；2点P为线段AB上方抛物线

7、上的任意一点，过点P作AB的垂线交AB于点H，点F为y轴上一点，当PBE的面积最大时，求PH+HF+FO的最小值；3在2中，PH+HF+FO取得最小值时，将CFH绕点C顺时针旋转60°后得到CFH，过点F'作CF的垂线与直线AB交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点D，Q，R，S为顶点的四边形为菱形，假设存在，请直接写出点S的坐标，假设不存在，请说明理由9.在RtABC中，A=90°，AC=AB=4， D，E分别是AB，AC的中点假设等腰RtADE绕点A逆时针旋转，得到等腰RtAD1E1，设旋转角为0<180°，记直线BD1与CE1的交点为P1如图1，当=90°时，线段BD1的长