静力学 第04章

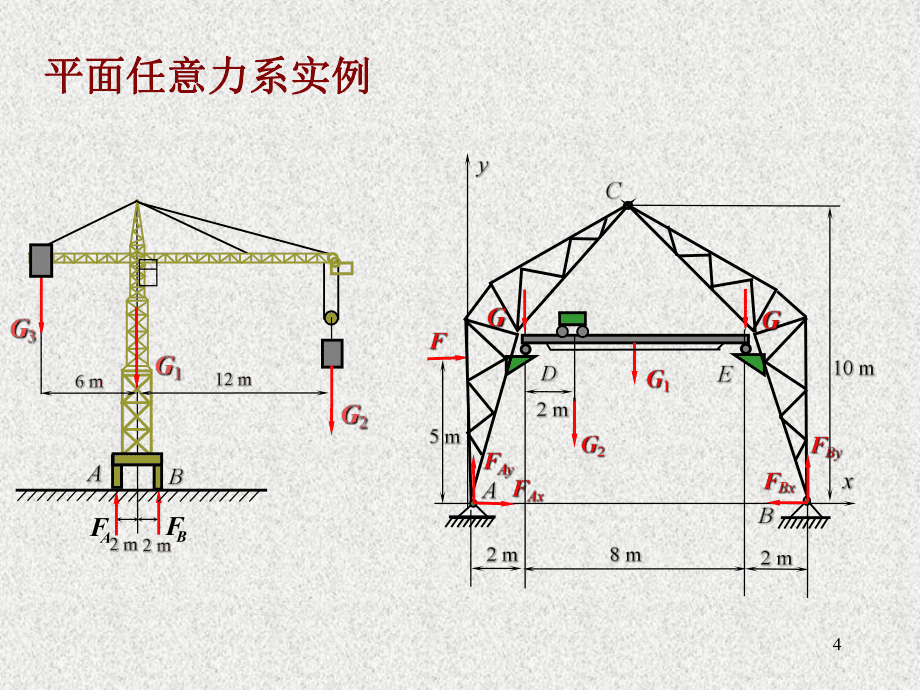
1、第四章 平面任意力系2第第4 4章章 平面任意力系平面任意力系平面任意力系平面任意力系：各力的作用线在同一平面内，既不汇交为一点又不相互平行的力系叫 。例例力系向一点简化力系向一点简化：把未知力系（平面任意力系）变成已知 力系（平面汇交力系和平面力偶系）3平面任意力系实例平面任意力系实例4AFBF平面任意力系实例平面任意力系实例5第第4章章 平面任意力系平面任意力系 41 力线平移定理力线平移定理 42 平面一般力系向一点简化平面一般力系向一点简化 43 平面一般力系的简化结果平面一般力系的简化结果 合力矩定理合力矩定理 44 平面一般力系的平衡条件和平衡方程平面一般力系的平衡条件和平衡方程

2、45 平面平行力系的平衡方程平面平行力系的平衡方程 46 静定与静不定问题的概念静定与静不定问题的概念物体系统的平衡物体系统的平衡 47 平面简单桁架的内力分析平面简单桁架的内力分析 48 平面一般力系习题课平面一般力系习题课64-1 4-1 力平移定理力平移定理力的平移定理力的平移定理：可以把作用在刚体上点可以把作用在刚体上点A的力的力 平行移到任一平行移到任一 点点B，但必须同时附加一个力偶。这个力偶，但必须同时附加一个力偶。这个力偶 的矩等于原来的力的矩等于原来的力 对新作用点对新作用点B的矩。的矩。FF证证 力力 力系力系），力偶（力FFF FFF ,F7力线平移定理揭示了力与力偶的关

3、系：力力线平移定理揭示了力与力偶的关系：力 力力+力偶力偶 （例断丝锥）（例断丝锥）力平移的条件是附加一个力偶力平移的条件是附加一个力偶m，且，且m与与d有关，有关，m=Fd 力线平移定理是力系简化的理论基础。力线平移定理是力系简化的理论基础。说明说明：84-2 4-2 平面一般力系向一点简化平面一般力系向一点简化 一般力系（任意力系）一般力系（任意力系）向一点简化向一点简化汇交力系汇交力系+力偶系力偶系 （未知力系） （已知力系） 汇交力系 力 ， R(主矢主矢) ， (作用在简化中心) 力 偶 系 力偶 ，MO (主矩主矩) ， (作用在该平面上) 9 大小大小： 主矢主矢 方向方向： 简

4、化中心简化中心 (与简化中心位置无关) 因主矢等于各力的矢量和RiFFFFR321主矢)()()( 21321iOOOOFmFmFmmmmM主矩2222)()(YXRRRyxXYRRxy11tgtg（移动效应移动效应）10 大小大小： 主矩主矩MO 方向方向： 方向规定 + 简化中心简化中心： (与简化中心有关) （因主矩等于各力对简化中心取矩的代数和）)(iOOFmM（转动效应转动效应）固定端（插入端）约束固定端（插入端）约束在工程中常见的雨 搭车 刀11固定端（插入端）约束固定端（插入端）约束说明说明 认为认为Fi这群力在同一这群力在同一 平面内平面内; 将将Fi向向A点简化得一点简化得一

5、 力和一力偶力和一力偶; RA方向不定可用正交方向不定可用正交 分力分力YA, XA表示表示; YA, XA, MA为固定端为固定端 约束反力约束反力; YA, XA限制物体平动限制物体平动, MA为限制转动。为限制转动。12平面一般力系的简化结果平面一般力系的简化结果 合力矩定理合力矩定理简化结果： 主矢 ，主矩 MO ，下面分别讨论。 =0,MO0 即简化结果为一合力偶, MO=M 此时刚 体等效于只有一个力偶的作用，因为力偶可以在刚体平 面内任意移动，故这时，主矩与简化中心O无关。R =0， MO =0，则力系平衡,下节专门讨论。 RR 0,MO =0,即简化为一个作用于简化中心的合力。

6、这时， 简化结果就是合力（这个力系的合力）, 。（此时 与简化中心有关，换个简化中心，主矩不为零）RRR13R 0,MO 0,为最一般的情况。此种情况还可以继续简可以继续简 化为一个合力化为一个合力 。R合力合力 的大小等于原力系的主矢的大小等于原力系的主矢合力合力 的作用线位置的作用线位置RMdORR14结论结论：)(1niiOOFmM)()(主矩OOMdRRm)()(1niiOOFmRM 平面任意力系的简化结果平面任意力系的简化结果 ：合力偶合力偶MO ； 合力合力 合力矩定理合力矩定理：由于主矩 而合力对O点的矩 合力矩定理 由于简化中心是任意选取的，故此式有普遍意义。 即：平面任意力系

7、的合力对作用面内任一点之矩等于力系平面任意力系的合力对作用面内任一点之矩等于力系 中各力对于同一点之矩的代数和。中各力对于同一点之矩的代数和。R15 xlq xdxqlxqx. . 求合力作用线位置；用分力矩计算合力矩。例：例：求合力作用线位置。解：解：合力Q对A点的力矩：ccAxqlxQM2 分布力对A点的力矩： loloxqldxxlqxdxq 223由合力矩定理：lxqlxqlcc32 322 xcc164-3 4-3 平面任意力系的平衡条件平面任意力系的平衡条件 由于 =0 为力平衡 MO=0 为力偶也平衡R所以平面任意力系平衡的充要条件为平面任意力系平衡的充要条件为： 力系的主矢力系

8、的主矢 和主矩和主矩 MO 都等于零都等于零，即： 0)()(22YXR0)(iOOFmMR170X0)(iAFm0)(iBFm二矩式二矩式条件：条件：x 轴不轴不 AB 连线连线0)(iAFm0)(iBFm0)(iCFm三矩式三矩式条件：条件：A,B,C不在不在 同一直线上同一直线上上式有三个独立方程，只能求出三个未知数。上式有三个独立方程，只能求出三个未知数。0X0Y0)(iOFm一矩式一矩式18 例例 已知：P, a , 求：A、B两点的支座反力？解：选AB梁研究 画受力图（以后注明 解除约束，可把支反 力直接画在整体结构 的原图上）0)(iAFm由32 , 032PNaNaPBB0X0

9、AX0Y3 , 0PYPNYABA解除约束19例题例题2021FB = 12 456 N2223q例题例题24q25 lq60G例题例题26B 60 q60GlqF3211 27B 6028设有F1, F2 Fn 各平行力系， 向O点简化得： 合力作用线的位置为： 平衡的充要条件为 主矢 =0 主矩MO =0 FxFRMxiiORRFRRO主矢iiiOOxFFmM)(主矩平面平行力系平面平行力系:各力的作用线在同一平面内且相互平行的力系叫 。平面平行力系的平衡方程平面平行力系的平衡方程29所以 平面平行力系的平衡方程为：0)(iAFm0)(iBFm 二矩式二矩式条件：条件：AB连线不能平行连线

10、不能平行 于力的作用线于力的作用线0Y0)(iOFm 一矩式一矩式实质上是各力在x 轴上的投影恒等于零，即 恒成立 ，所以只有两个独立方程，只能求解两个独立的未知数。0X300, 0AXX由022; 0)(aPmaaqaRFmBA0Y0PqaRYBA)kN(122028 .01628 .02022PamqaRB)kN(24128 .02020BARqaPY例例 已知：P=20kN, m=16kNm, q=20kN/m, a=0.8m 求：A、B的支反力。解：研究AB梁解得：31平面平行力系的平衡方程也可用两矩式表示，即0)(iAFm0)(iBFm其中：其中：A、B两点的连线两点的连线必须不与各

11、力线平行必须不与各力线平行例例 已知：塔式起重机 P=700kN, W=200kN (最大起重量)，尺寸如图。求：保证满载和空载时不致翻倒，平衡块Q=？ 当Q=180kN时，求满载时轨道A、B给起重机轮子的反力？320)(FmB0) 22() 212(2) 26(ANWPQ0ANkN 75Q限制条件限制条件：解得解得解解： 首先考虑满载时，起首先考虑满载时，起重机不向右翻倒的最小重机不向右翻倒的最小Q为：为：空载时，空载时，W=0由0)(FmA0) 22(2) 26(BNPQ限制条件限制条件为：0BN解得解得kN 350Q因此保证空、满载均不倒因此保证空、满载均不倒Q应满足如下关系应满足如下关

12、系：kN 350kN 75Q3304) 212(2) 26 (BNWPQ0)(FmA, 0iF0BANNWPQkN 870,kN 210BANN求当求当Q=180kN，满载，满载W=200kN时，时，NA ,NB为多少为多少 由平面平行力系的平衡方程可得：由平面平行力系的平衡方程可得： 解得：解得：34一、刚化原理： 变形体在已知力的作用下处于平衡，若将变形后的变形体换成刚体（钢化），则平衡状态不变。 刚体的平衡条件是变形体平衡的必要条件，不是充分条件。4-4 4-4 刚体系的平衡刚体系的平衡35物体系：物体系：由几个物体组成的系统,它们之间通过约束相连。个物体组成的系统个物体组成的系统: :

13、最多有个平衡方程,最多可解个未知量。二、刚体系统的平衡二、刚体系统的平衡36例例 外力外力：外界物体作用于系统上的力叫外力。内力内力：系统内部各物体之间的相互作用力叫内力。37物系平衡的特点：物系平衡的特点： 物系静止物系静止 物系中每个单体也是平衡的。每个单体可列物系中每个单体也是平衡的。每个单体可列3 3个个 平衡方程，整个系统可列平衡方程，整个系统可列3 3n个方程（设物系中个方程（设物系中 有有n个物体）个物体）解物系问题的一般方法：解物系问题的一般方法： 由整体由整体 局部局部（常用），由局部由局部 整体整体（用较少）38例：例：求A、B、C三点约束反力。解：1）研究对象：Q=q2=

14、30kNABRARBCYCmmcXCRBBq=15kN/mm=20kNmAB1 m2 m2 mC2）画受力图3）列平衡方程求解：AB 、BC39kNRQR:mAAB100130 Q=q2=30kN1 m2 mkNRQRR:YBAB2000 ) (kNRQR:mBBA200230 40kNRRBB20 2 m00 CX:X kNYRY:YCBC2000 mkNmmYm:mCCCB 60020 ) ( mkNmmRm:mCBCC 6002041例例 已知：OA=R, AB= l , 当OA水平时，冲压力为P时， 求：M=？O点的约束反力？AB杆内力？冲头给导轨的侧压力？0X由0sin BSN0Y0

15、cosBSPgPNPSB t ,cos解解：研究B420)(FmO0cosMRSA0X0sin AOSX0Y0cosOAYSPRM PYO tgPXO负号表示力的方向与图中所设方向相反再研究轮43例例 已知：连续梁上，P=10kN, Q=50kN, CE 铅垂, 不计梁重 求：A ,B和D点的反力（看出未知数多余三个，不能先整 体求出，要拆开） 0Fm由0512PQYG)kN(50210550GY解解：研究起重机440Cm由016GDYY)kN(33. 8650DY0610123, 0QPYYmDBA)kN(100BY0, 0PQYYYYDBA)kN(33.48AY 再研究整体 再研究梁CD4

16、5解解： 选整体研究 受力如图 选坐标、取矩点、Bxy,B点 列方程为: 解方程得 0X; 0BX0Bm0DEPMB)mN(100011000BM 0Y; 0PYBPYB 例例1 已知各杆均铰接，B端插入地内，P=1000N，AE=BE=CE=DE=1m，杆重不计。 求AC 杆内力？B点的反力？八、例题分析八、例题分析46 受力如图 取E为矩心，列方程 解方程求未知数045sin, 0EDPCESmoCAE)N(14141707. 01100045sinCEEDPSoCA再研究CD杆47例例2 已知已知:P=100N. AC=1.6m,BC=0.9m,CD=EC=1.2m,AD=2m 且AB水

17、平, ED铅垂,BD垂直于 斜面； 求求 ?和支座反力？解解： 研究整体 画受力图 选坐标列方程 BDS02 . 15 . 2, 0PYmAB0sincossin , 0PYXXAA5322 . 1 cos ;5426 . 1 sinADCDADAC而N48 ;N136 :AAYX解得48再研究AB杆，受力如图0sin , 0ACYCBSmABC由N7 .106549 . 06 . 1)48(sin:BCACYSAB解得49平面一般力系习题课平面一般力系习题课一、力线平移定理是力系简化的理论基础一、力线平移定理是力系简化的理论基础 力 力+力偶 平衡; 0, 0OMR合力矩定理合力矩定理)()

18、(1iniOOFmRm; 0, 0; 0, 0OOMRMR或合力（主矢）; 0, 0OMR合力偶（主矩） 二、平面一般力系的合成结果二、平面一般力系的合成结果本章小结：本章小结：50一矩式一矩式 二矩式二矩式 三矩式三矩式三、三、 0)(00FmYXO0)(0)(0FmFmXBAA,B连线不连线不 x轴轴0)(0)(0)(FmFmFmCBAA,B,C不共线不共线平面一般力系的平衡方程平面一般力系的平衡方程平面平行力系的平衡方程平面平行力系的平衡方程 成为恒等式 一矩式 二矩式 0X0)(0FmYA0)(0)(FmFmBABA连线不平行于力线51平面汇交力系的平衡方程平面汇交力系的平衡方程 成为恒等式 0)(FmA00YX平面力偶系的平衡方程平面力偶系的平衡方程0im四、静定与静不定四、静定与静不定 独立方程数 未知力数目为静定 独立方程数 = 未知力数目为静不定五、物系平衡五、物系平衡 物系平衡时，物系中每个构件都平衡， 解物系问题的方法常是：由整体由整体 局部局部 单体单体52六、解题步骤与技