四川省南充市中考数学模拟试卷5月含答案解析word版

1、2016年四川省南充市中考数学模拟试卷（5月份）一、选择题（共10小题，每小题3分，满分30分，每小题只有一个正确的选项，请在答题卡的相应位置填涂）18的相反数是（）A8B8C D2在一次射击测试中，甲、乙、丙、丁的平均环数均相同，而方差分别为8.7，6.5，9.1，7.7，则这四人中，射击成绩最稳定的是（）A甲B乙C丙D丁3如图，为一个多面体的表面展开图，每个面内都标注了数字若数字为6的面是底面，则朝上一面所标注的数字为（）A5B4C3D24下列四边形：正方形、矩形、菱形，对角线一定相等的是（）ABCD5不等式组的解是（）Ax1Bx2C1x2D无解6如图，AC，BD是O直径，且ACBD，动点

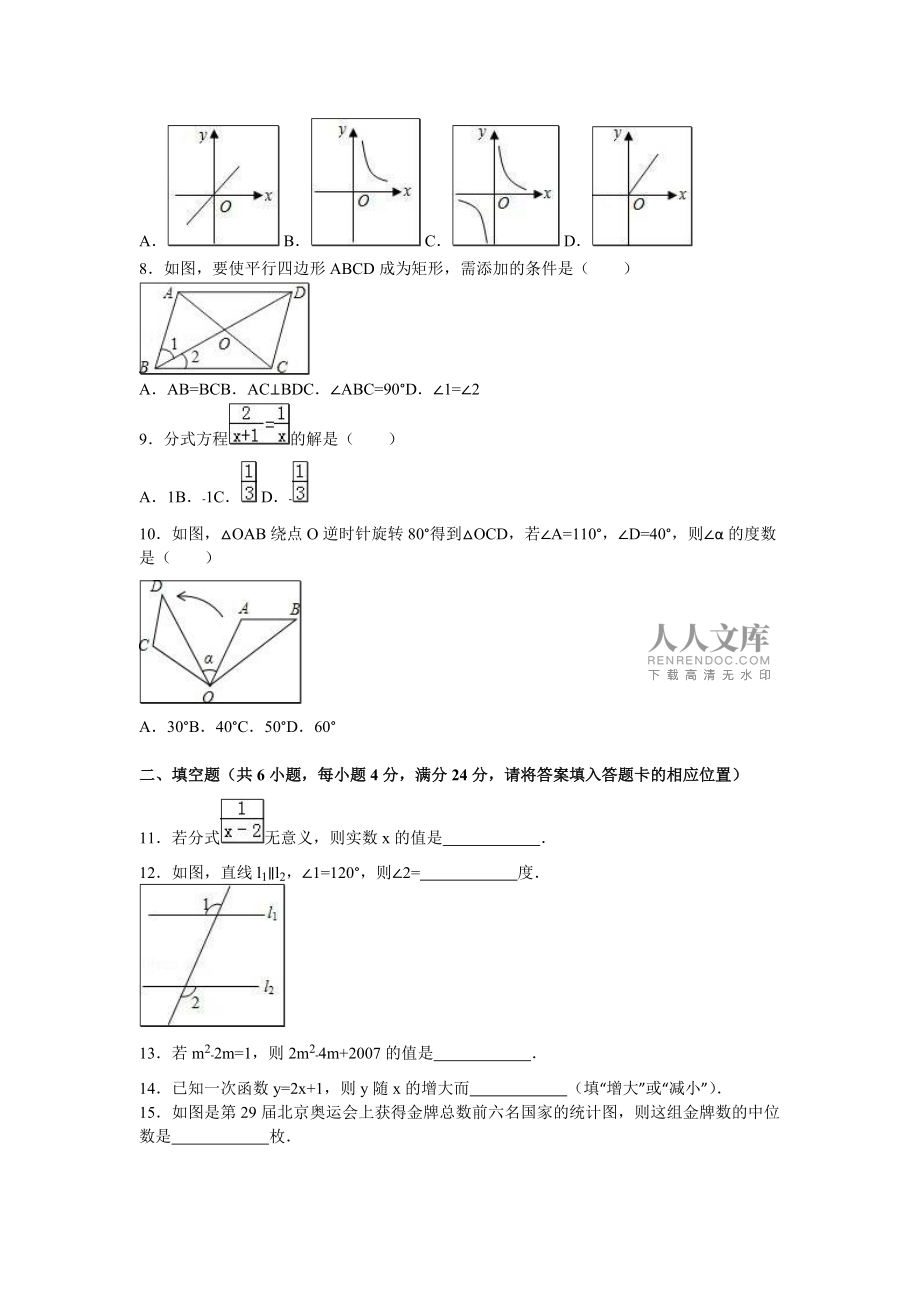
2、P从圆心O出发，沿OCDO路线作匀速运动，设运动时间为t（秒），APB=y（度），则下列图象中表示y与t之间的函数关系最恰当的是（）A B C D7矩形面积为4，它的长y与宽x之间的函数关系用图象大致可表示为（）A B C D8如图，要使平行四边形ABCD成为矩形，需添加的条件是（）AAB=BCBACBDCABC=90D1=29分式方程的解是（）A1B1C D10如图，OAB绕点O逆时针旋转80得到OCD，若A=110，D=40，则的度数是（）A30B40C50D60二、填空题（共6小题，每小题4分，满分24分，请将答案填入答题卡的相应位置）11若分式无意义，则实数x的值是12如图，直线l1l

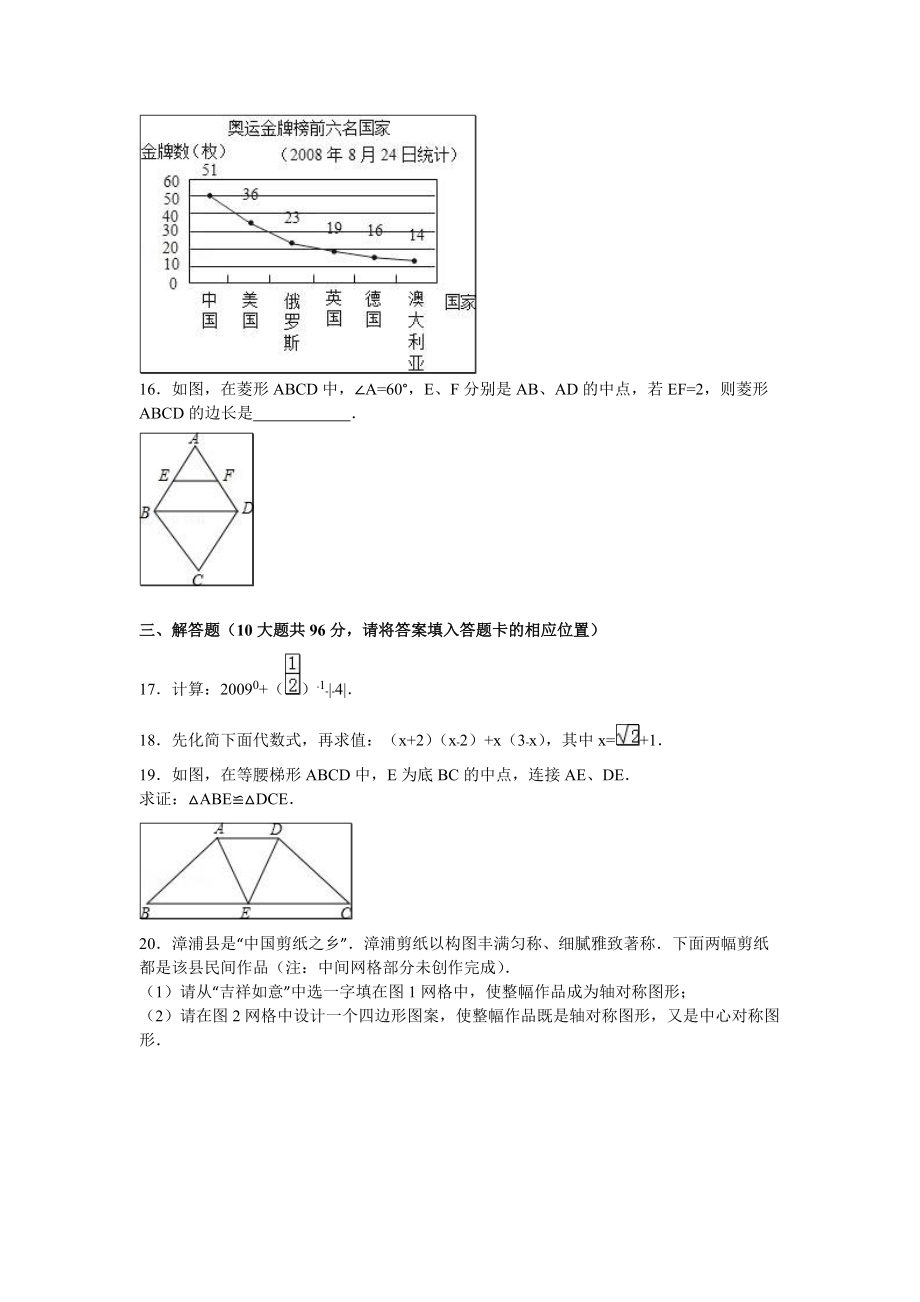
3、2，1=120，则2=度13若m22m=1，则2m24m+2007的值是14已知一次函数y=2x+1，则y随x的增大而（填“增大”或“减小”）15如图是第29届北京奥运会上获得金牌总数前六名国家的统计图，则这组金牌数的中位数是枚16如图，在菱形ABCD中，A=60，E、F分别是AB、AD的中点，若EF=2，则菱形ABCD的边长是三、解答题（10大题共96分，请将答案填入答题卡的相应位置）17计算：20090+（）1|4|18先化简下面代数式，再求值：（x+2）（x2）+x（3x），其中x=+119如图，在等腰梯形ABCD中，E为底BC的中点，连接AE、DE求证：ABEDCE20漳浦县是“中国剪

4、纸之乡”漳浦剪纸以构图丰满匀称、细腻雅致著称下面两幅剪纸都是该县民间作品（注：中间网格部分未创作完成）（1）请从“吉祥如意”中选一字填在图1网格中，使整幅作品成为轴对称图形；（2）请在图2网格中设计一个四边形图案，使整幅作品既是轴对称图形，又是中心对称图形21如图，点D在O的直径AB的延长线上，点C在O上，AC=CD，D=30，（1）求证：CD是O的切线；（2）若O的半径为3，求的长（结果保留）22阅读材料，解答问题利用图象法解一元二次不等式：x22x30解：设y=x22x3，则y是x的二次函数a=10，抛物线开口向上又当y=0时，x22x3=0，解得x1=1，x2=3由此得抛物线y=x22x

5、3的大致图象如图所示观察函数图象可知：当x1或x3时，y0x22x30的解集是：x1或x3（1）观察图象，直接写出一元二次不等式：x22x30的解集是；（2）仿照上例，用图象法解一元二次不等式：x210（大致图象画在答题卡上）23为了防控甲型H1N1流感，某校积极进行校园环境消毒，购买了甲、乙两种消毒液共100瓶，其中甲种6元/瓶，乙种9元/瓶（1）如果购买这两种消毒液共用780元，求甲、乙两种消毒液各购买多少瓶？（2）该校准备再次购买这两种消毒液（不包括已购买的100瓶），使乙种瓶数是甲种瓶数的2倍，且所需费用不多于1200元（不包括780元），求甲种消毒液最多能再购买多少瓶？24小红与小刚

6、姐弟俩做掷硬币游戏，他们两人同时各掷一枚壹元硬币（1）若游戏规则为：当两枚硬币落地后正面朝上时，小红赢，否则小刚赢请用画树状图或列表的方法，求小刚赢的概率；（2）小红认为上面的游戏规则不公平，于是把规则改为：当两枚硬币正面都朝上时，小红得8分，否则小刚得4分那么，修改后的游戏规则公平吗？请说明理由；若不公平，请你帮他们再修改游戏规则，使游戏规则公平（不必说明理由）25几何模型：条件：如图，A、B是直线l同旁的两个定点问题：在直线l上确定一点P，使PA+PB的值最小方法：作点A关于直线l的对称点A，连结AB交l于点P，则PA+PB=AB的值最小（不必证明）模型应用：（1）如图1，正方形ABCD的

7、边长为2，E为AB的中点，P是AC上一动点连结BD，由正方形对称性可知，B与D关于直线AC对称连结ED交AC于P，则PB+PE的最小值是；（2）如图2，O的半径为2，点A、B、C在O上，OAOB，AOC=60，P是OB上一动点，求PA+PC的最小值；（3）如图3，AOB=45，P是AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求PQR周长的最小值26如图1，已知：抛物线y=+bx+c与x轴交于A、B两点，与y轴交于点C，经过B、C两点的直线是y=x2，连结AC（1）B、C两点坐标分别为B（，）、C（，），抛物线的函数关系式为；（2）判断ABC的形状，并说明理由；（3）若ABC内部能

8、否截出面积最大的矩形DEFC（顶点D、E、F、G在ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由抛物线y=ax2+bx+c的顶点坐标是2016年四川省南充市中考数学模拟试卷（5月份）参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分，每小题只有一个正确的选项，请在答题卡的相应位置填涂）18的相反数是（）A8B8C D【考点】相反数【分析】根据相反数的概念，互为相反数的两个数和为0，即可得出答案【解答】解：根据概念可知8+（8的相反数）=0，所以8的相反数是8故选A2在一次射击测试中，甲、乙、丙、丁的平均环数均相同，而方差分别为8.7，6.5，9.1，7.

9、7，则这四人中，射击成绩最稳定的是（）A甲B乙C丙D丁【考点】方差【分析】方差就是各变量值与其均值离差平方的平均数，反映了一组数据的波动情况方差越小，射击成绩越稳定【解答】解：因为S甲2=8.7，S乙2=6.5，S丙2=9.1，S丁2=7.7所以S丙2S甲2S丁2S乙2，所以射击成绩最稳定的是乙故选B3如图，为一个多面体的表面展开图，每个面内都标注了数字若数字为6的面是底面，则朝上一面所标注的数字为（）A5B4C3D2【考点】专题：正方体相对两个面上的文字【分析】利用正方体及其表面展开图的特点解题【解答】解：这是一个长方体的平面展开图，共有六个面，其中面“6”与面“2”相对，面“5”与面“3”

10、相对，面“4”与面“1”相对所以若数字为6的面是底面，则朝上一面所标注的数字为2故选D4下列四边形：正方形、矩形、菱形，对角线一定相等的是（）ABCD【考点】正方形的性质；菱形的性质；矩形的性质【分析】根据正方形，矩形及菱形的性质，从而可得到最后答案【解答】解：根据矩形的性质，矩形的对角线把矩形分为两个直角三角形，根据勾股定理，对角线相等，正方形属于特殊的矩形，对角线相等，故选B5不等式组的解是（）Ax1Bx2C1x2D无解【考点】解一元一次不等式组【分析】分别解不等式组中的两个不等式，得出x的取值范围，取其公共范围即可得出结论【解答】解：解不等式x10，得：x1；解不等式2x4，得：x2不等

11、式组的解集为1x2故选C6如图，AC，BD是O直径，且ACBD，动点P从圆心O出发，沿OCDO路线作匀速运动，设运动时间为t（秒），APB=y（度），则下列图象中表示y与t之间的函数关系最恰当的是（）A B C D【考点】动点问题的函数图象【分析】根据题意，分P在OC、CD、DO之间3个阶段，分别分析变化的趋势，又由点P作匀速运动，故都是线段，分析选项可得答案【解答】解：根据题意，分3个阶段；P在OC之间，APB逐渐减小，到C点时，为45，P在CD之间，APB保持45，大小不变，P在DO之间，APB逐渐增大，到O点时，为90；又由点P作匀速运动，故都是线段；分析可得：C符合3个阶段的描述；故选

12、：C7矩形面积为4，它的长y与宽x之间的函数关系用图象大致可表示为（）A B C D【考点】反比例函数的应用；反比例函数的图象【分析】首先由矩形的面积公式，得出它的长y与宽x之间的函数关系式，然后根据函数的图象性质作答注意本题中自变量x的取值范围【解答】解：由矩形的面积4=xy，可知它的长y与宽x之间的函数关系式为y=（x0），是反比例函数图象，且其图象在第一象限故选B8如图，要使平行四边形ABCD成为矩形，需添加的条件是（）AAB=BCBACBDCABC=90D1=2【考点】矩形的判定；平行四边形的性质【分析】根据一个角是90度的平行四边形是矩形进行选择即可【解答】解：A、是邻边相等，可判定

13、平行四边形ABCD是菱形；B、是对角线互相垂直，可判定平行四边形ABCD是菱形；C、是一内角等于90，可判断平行四边形ABCD成为矩形；D、是对角线平分对角，可判定平行四边形ABCD是菱形故选C9分式方程的解是（）A1B1C D【考点】解分式方程【分析】本题考查解分式方程的能力，观察方程可得最简公分母为x（x+1）【解答】解：去分母得2x=x+1，解得x=1将x=1代入x（x+1）=20，则方程的解为x=1故选A10如图，OAB绕点O逆时针旋转80得到OCD，若A=110，D=40，则的度数是（）A30B40C50D60【考点】旋转的性质【分析】根据旋转的意义，图片按逆时针方向旋转80，可得A

14、OC=80，又有A=110，D=40，根据图形可得，=AOCDOC；代入数据可得答案【解答】解：根据旋转的意义，图片按逆时针方向旋转80，即AOC=80，又A=110，D=40，DOC=30，则=AOCDOC=50故选C二、填空题（共6小题，每小题4分，满分24分，请将答案填入答题卡的相应位置）11若分式无意义，则实数x的值是2【考点】分式有意义的条件【分析】因为分式无意义，所以x2=0，即可解得x的值【解答】解：根据题意得：x2=0，即x=2故答案为212如图，直线l1l2，1=120，则2=120度【考点】平行线的性质；对顶角、邻补角【分析】由l1l2可以得到1=3=120，又由3=2可以

15、得到2的度数【解答】解：l1l2，1=3=120，3=2，2=120故填空答案：12013若m22m=1，则2m24m+2007的值是2009【考点】代数式求值【分析】只要把所求代数式化成已知的形式，然后把已知代入即可注意整体思想的应用【解答】解：原式=2m24m+2007=2（m22m）+2007把m22m=1代入上式得：21+2007=200914已知一次函数y=2x+1，则y随x的增大而增大（填“增大”或“减小”）【考点】一次函数的性质【分析】根据一次函数y=kx+b的图象的性质作答【解答】解：y=2x+1，k=20，y随x的增大而增大15如图是第29届北京奥运会上获得金牌总数前六名国家

16、的统计图，则这组金牌数的中位数是21枚【考点】中位数；折线统计图【分析】先根据题意把这一组数从小到大排列，然后根据中位数的定义求解【解答】解：从小到大排列为：14，16，19，23，36，51，根据中位数的定义知其中位数为（19+23）2=21这组金牌数的中位数是21（枚）故填2116如图，在菱形ABCD中，A=60，E、F分别是AB、AD的中点，若EF=2，则菱形ABCD的边长是4【考点】三角形中位线定理；菱形的性质【分析】ABD是等边三角形根据中位线定理易求BD【解答】解：在菱形ABCD中，A=60，AEF是等边三角形E、F分别是AB、AD的中点，AB=2AE=2EF=22=4故答案为，4

17、三、解答题（10大题共96分，请将答案填入答题卡的相应位置）17计算：20090+（）1|4|【考点】实数的运算；绝对值；零指数幂；负整数指数幂【分析】本题涉及零指数幂、负整数指数幂、绝对值三个考点在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果【解答】解：原式=1+24=118先化简下面代数式，再求值：（x+2）（x2）+x（3x），其中x=+1【考点】整式的混合运算化简求值【分析】先利用平方差公式和单项式乘多项式的法则化简，然后代入数据计算求值【解答】解：（x+2）（x2）+x（3x），=x24+3xx2，=3x4，当x=+1时，原式=3（+1）4=3119如图，

18、在等腰梯形ABCD中，E为底BC的中点，连接AE、DE求证：ABEDCE【考点】等腰梯形的性质；全等三角形的判定【分析】等腰梯形的腰相等，同一底上的两个角相等，容易知道AB=DC，B=C，又BE=CE，所以容易证明ABEDCE【解答】证明：四边形ABCD是等腰梯形，AB=DC，B=CE为BC的中点，BE=ECABEDCE20漳浦县是“中国剪纸之乡”漳浦剪纸以构图丰满匀称、细腻雅致著称下面两幅剪纸都是该县民间作品（注：中间网格部分未创作完成）（1）请从“吉祥如意”中选一字填在图1网格中，使整幅作品成为轴对称图形；（2）请在图2网格中设计一个四边形图案，使整幅作品既是轴对称图形，又是中心对称图形【

19、考点】利用旋转设计图案；利用轴对称设计图案【分析】（1）“吉祥如意”四个字中，只有吉是轴对称图形；（2）作一个轴对称图形，使对称轴过原来图形的中心即可【解答】解：（1）吉（符合要求就给分）（2）有多种画法，只要符合要求就给分21如图，点D在O的直径AB的延长线上，点C在O上，AC=CD，D=30，（1）求证：CD是O的切线；（2）若O的半径为3，求的长（结果保留）【考点】切线的判定；弧长的计算【分析】（1）根据等腰三角形得出得出A=D，A=ACO，求出A=ACO=30，求出COD=60，根据三角形内角和定理求出OCD，根据切线的判定推出即可；（2）根据弧长公式l=求出即可【解答】（1）证明：连

20、接OC，AC=CD，D=30，A=D=30，OA=OC，A=ACO=30，DOC=A+ACO=60，OCD=1803060=90，OCCD，OC为O半径，CD是O的切线；（2）解：O半径是3，BOC=60，由弧长公式得：的长为： =22阅读材料，解答问题利用图象法解一元二次不等式：x22x30解：设y=x22x3，则y是x的二次函数a=10，抛物线开口向上又当y=0时，x22x3=0，解得x1=1，x2=3由此得抛物线y=x22x3的大致图象如图所示观察函数图象可知：当x1或x3时，y0x22x30的解集是：x1或x3（1）观察图象，直接写出一元二次不等式：x22x30的解集是；（2）仿照上例

21、，用图象法解一元二次不等式：x210（大致图象画在答题卡上）【考点】二次函数与不等式（组）【分析】（1）由x22x3=0得x1=1，x2=3，抛物线y=x22x3开口向上，y0时，图象在x轴的下方，此时1x3；（2）仿照（1）的方法，解出图象与x轴的交点坐标，根据图象的开口方向及函数值的符号，确定x的范围【解答】解：（1）1x3；（2）设y=x21，则y是x的二次函数，a=10，抛物线开口向上又当y=0时，x21=0，解得x1=1，x2=1由此得抛物线y=x21的大致图象如图所示观察函数图象可知：当x1或x1时，y0x210的解集是：x1或x123为了防控甲型H1N1流感，某校积极进行校园环境

22、消毒，购买了甲、乙两种消毒液共100瓶，其中甲种6元/瓶，乙种9元/瓶（1）如果购买这两种消毒液共用780元，求甲、乙两种消毒液各购买多少瓶？（2）该校准备再次购买这两种消毒液（不包括已购买的100瓶），使乙种瓶数是甲种瓶数的2倍，且所需费用不多于1200元（不包括780元），求甲种消毒液最多能再购买多少瓶？【考点】二元一次方程组的应用；一元一次不等式的应用【分析】（1）等量关系为：甲消毒液总价钱+乙消毒液总价钱=780（2）关系式为：甲消毒液总价钱+乙消毒液总价钱1200【解答】解：（1）设甲种消毒液购买x瓶，则乙种消毒液购买瓶依题意得：6x+9=780解得：x=40100x=10040=6

23、0（瓶）答：甲种消毒液购买40瓶，乙种消毒液购买60瓶（2）设再次购买甲种消毒液y瓶，则购买乙种消毒液2y瓶依题意得：6y+92y1200解得：y50答：甲种消毒液最多再购买50瓶24小红与小刚姐弟俩做掷硬币游戏，他们两人同时各掷一枚壹元硬币（1）若游戏规则为：当两枚硬币落地后正面朝上时，小红赢，否则小刚赢请用画树状图或列表的方法，求小刚赢的概率；（2）小红认为上面的游戏规则不公平，于是把规则改为：当两枚硬币正面都朝上时，小红得8分，否则小刚得4分那么，修改后的游戏规则公平吗？请说明理由；若不公平，请你帮他们再修改游戏规则，使游戏规则公平（不必说明理由）【考点】游戏公平性；列表法与树状图法【分

24、析】列举出符合题意的各种情况的个数，再根据概率公式解答，比较即可【解答】解：（1）由树状图可知共有22=4种可能，两枚硬币落地后正面朝上的有1种，所以概率是，所以小红赢的概率是，小刚赢的概率为；（2）每次游戏小红平均得到的分数为：8=2，小刚得到的分数为：4=3，修改后游戏也不公平应该修改为：当两枚硬币正面都朝上时，小红得3分，否则小刚得1分25几何模型：条件：如图，A、B是直线l同旁的两个定点问题：在直线l上确定一点P，使PA+PB的值最小方法：作点A关于直线l的对称点A，连结AB交l于点P，则PA+PB=AB的值最小（不必证明）模型应用：（1）如图1，正方形ABCD的边长为2，E为AB的中

25、点，P是AC上一动点连结BD，由正方形对称性可知，B与D关于直线AC对称连结ED交AC于P，则PB+PE的最小值是sqrt5；（2）如图2，O的半径为2，点A、B、C在O上，OAOB，AOC=60，P是OB上一动点，求PA+PC的最小值；（3）如图3，AOB=45，P是AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求PQR周长的最小值【考点】圆的综合题【分析】（1）由题意可知，连接ED交AC于点P，此时PB+PE最小值是ED的长度，由勾股定理即可求出ED的长为；（2）延长AO交O于点D，连接DC，AC，此时PA+PC的最小值为DC的长度，利用勾股定理即可求出DC的长度为；（3）要求

26、PQR周长的最小值，即求PR+QR+PQ的最小值即可，作点C，使得点P与点C关于OB对称，作点D，使得点P与点D关于OA对称，连接OC、OD、CD，CD交OA、OB于点Q、R，此时PR+QR+PQ最小，且PR+QR+PQ=CD，即求出CD的长即可【解答】解：（1）由题意知：连接ED交AC于点P，此时PB+PE最小，最小值为ED，点E是AB的中点，AE=1，由勾股定理可知：ED2=AE2+AD2=5，ED=，PB+PE的最小值为；（2）延长AO交O于点D，连接DC，AC，AD=4，AOC=60，OA=OC，AOC是等边三角形，AC=OA=2，AD是O直径，ACD=90，由勾股定理可求得：CD=2

27、，PA+PC的最小值为2；（3）作点C，使得点P与点C关于OB对称，作点D，使得点P与点D关于OA对称，连接OC、OD、CD，CD交OA、OB于点Q、R，此时PR+RQ+PQ最小，最小值为CD的长，点P与点C关于OB对称，BOP=COB，OP=OC=10，同理，DOA=POA，OP=OD=10，BOP+POA=45，COD=2（BOP+POA）=90，由勾股定理可知：CD=10，PQR周长的最小值为1026如图1，已知：抛物线y=+bx+c与x轴交于A、B两点，与y轴交于点C，经过B、C两点的直线是y=x2，连结AC（1）B、C两点坐标分别为B（4，0）、C（0，2），抛物线的函数关系式为y=

28、frac12x2frac32x2；（2）判断ABC的形状，并说明理由；（3）若ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由抛物线y=ax2+bx+c的顶点坐标是【考点】二次函数综合题【分析】（1）先利用一次函数解析式和坐标轴上点的坐标特征确定C点和B点坐标，然后把C点和B点坐标代入y=+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；（2）先解方程x2x2=0确定A（1，0），再利用两点间的距离公式计算出AC2=5，BC2=20，AB2=25，然后根据勾股定理的逆定理可证明ABC是直角三角形；（3）分类讨论：当矩形DEFG顶点D