大学物理课件稳恒电流

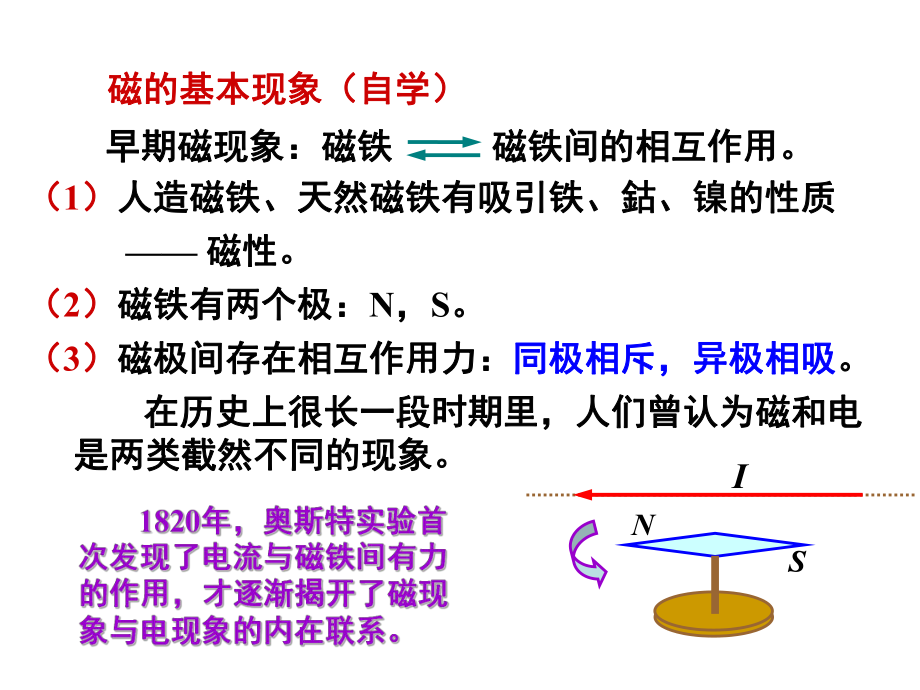
1、10.1 10.1 磁场，磁感应强度磁场，磁感应强度（steady magnetic field） 不随时间变化不随时间变化的磁场称为的磁场称为稳恒磁场稳恒磁场，有时也，有时也称为称为“静磁场静磁场”。 稳恒电流稳恒电流激发的磁场就是一种激发的磁场就是一种稳恒磁场稳恒磁场。 一方面，一方面，运动的电荷（或电流）要产生磁场；运动的电荷（或电流）要产生磁场；另一方面，另一方面，磁场又会对其他的运动电荷（或电流）磁场又会对其他的运动电荷（或电流）有作用力。有作用力。 本章就从这两个方面来研究磁场。本章就从这两个方面来研究磁场。稳恒磁场（1）人造磁铁、天然磁铁有吸引铁、鈷、镍的性质人造磁铁、天然磁铁有

2、吸引铁、鈷、镍的性质 磁性。磁性。（2）磁铁有两个极：磁铁有两个极：n，s。（3）磁极间存在相互作用力：磁极间存在相互作用力：同极相斥，异极相吸同极相斥，异极相吸。 在历史上很长一段时期里，人们曾认为磁和电在历史上很长一段时期里，人们曾认为磁和电是两类截然不同的现象。是两类截然不同的现象。ns早期磁现象：磁铁早期磁现象：磁铁 磁铁间的相互作用。磁铁间的相互作用。i磁的基本现象（自学）磁的基本现象（自学）奥斯特奥斯特（hans christan oersted，1777-1851） 丹麦物理学家，发现丹麦物理学家，发现了电流对磁针的作用，从了电流对磁针的作用，从而导致了而导致了19世纪中叶电磁世

3、纪中叶电磁理论的统一和发展。理论的统一和发展。 启发物理学家们提出这样的问题：启发物理学家们提出这样的问题：磁铁和电磁铁和电流是否本源上是一致的？流是否本源上是一致的？磁铁对载流导线磁铁对载流导线也有力的作用；也有力的作用；磁铁对运动电荷磁铁对运动电荷也有力的作用；也有力的作用；电流与电流之间电流与电流之间也有力的相互作用。也有力的相互作用。一切磁现象都起源于电荷的运动一切磁现象都起源于电荷的运动(电流电流)。磁场力磁场力就是运动电荷之间的一种相互作用力。就是运动电荷之间的一种相互作用力。 1882年，安培年，安培对这些实验事实进行分析的基对这些实验事实进行分析的基础上，础上，提出了物质磁性本

4、质的假说提出了物质磁性本质的假说：人们还发现：人们还发现：通电螺线管的通电螺线管的行为很象一块磁铁。行为很象一块磁铁。 奥斯特实验证明电流对磁铁有力的作用。奥斯特实验证明电流对磁铁有力的作用。 同时，人们还发现：同时，人们还发现：运动电荷运动电荷运动电荷运动电荷磁场磁场磁场和电场一样，也是物质存在的一种形式。磁场和电场一样，也是物质存在的一种形式。（1）磁场对引入磁场中的其他运动电荷或载流导体磁场对引入磁场中的其他运动电荷或载流导体有有磁力磁力的作用；的作用；（2）载流导体在磁场内移动时，磁场的作用力将对载流导体在磁场内移动时，磁场的作用力将对它它作功作功，说明磁场具有能量。，说明磁场具有能量

5、。 任何运动电荷或电流，在周围空间产生磁场，任何运动电荷或电流，在周围空间产生磁场，磁场对外的重要表现磁场对外的重要表现是：是：一、磁场一、磁场 描述磁场的是磁感应强度这一物理量，由于描述磁场的是磁感应强度这一物理量，由于历史的原因不叫磁场强度。历史的原因不叫磁场强度。它的定义方法有三种：它的定义方法有三种：（1）由试探电流元在磁场中受力来定义；由试探电流元在磁场中受力来定义；（2）由由运动电荷运动电荷在磁场中所受到的力来定义；在磁场中所受到的力来定义；（3）由试探线圈在磁场中受的力矩来定义。由试探线圈在磁场中受的力矩来定义。二、二、 磁感应强度磁感应强度 b 这三种定义是相互等效的，这三种定

6、义是相互等效的，我们现采用第二种我们现采用第二种方式来定义方式来定义磁感应强度磁感应强度 。bxyzo0f 磁感应强度磁感应强度 的定义的定义b+v 实验发现：实验发现：带电粒子带电粒子在磁场中沿某一特定直线在磁场中沿某一特定直线方向运动时不受力，此直方向运动时不受力，此直线方向与电荷无关。线方向与电荷无关。+vvv 将一个电量为将一个电量为 q 的点电荷以的点电荷以相同的速率相同的速率沿沿不同的不同的方向方向通过磁场中的某一点。发现：通过磁场中的某一点。发现：带电粒子在磁场中带电粒子在磁场中运动所受的力与运动方向有关运动所受的力与运动方向有关。带电粒子在磁场中沿其他方向运动时，带电粒子在磁场

7、中沿其他方向运动时， 垂直垂直于于 与特定直线所组成的平面。与特定直线所组成的平面。f 当带电粒子在磁场当带电粒子在磁场中垂直于此特定直线运动中垂直于此特定直线运动时受力最大。时受力最大。fffmax 磁感强度磁感强度 的定义：的定义：当当正电荷垂直于特定直线运动正电荷垂直于特定直线运动时，受力时，受力 ，将，将 方方向定义为该点的向定义为该点的 的的方向方向。 bmaxff maxb,max qfqfmax大小与大小与 无关无关q,单位单位 特斯拉特斯拉mn/a1)t( 1+qvbmaxfvqfbmax磁感强度磁感强度大小大小运动电荷在磁场中受力运动电荷在磁场中受力bqf v 磁感强度磁感强

8、度 的定义：的定义：当当正电荷正电荷垂直于特定直线运动垂直于特定直线运动时，受力时，受力 ，将，将 方方向定义为该点的向定义为该点的 的的方向方向。 bmaxff maxb10.2 10.2 磁通，磁场的高斯定理磁通，磁场的高斯定理规定：规定：（磁感应线密的地方磁场强；（磁感应线密的地方磁场强； 疏的地方磁场弱。）疏的地方磁场弱。）dsdnb静电场：静电场：磁磁 场：场：?dssb,/0 isqsde 1）磁感应线上每一点的切线方向与该点磁感应线上每一点的切线方向与该点 的方向一致。的方向一致。 b 2）通过某点垂直于通过某点垂直于 方向的单位面积上的磁感应线方向的单位面积上的磁感应线 条数等

9、于该点条数等于该点 的大小。的大小。bbbsd直线电流的磁感应线直线电流的磁感应线ibii圆电流的磁感应线圆电流的磁感应线bi通电螺线管的磁感应线通电螺线管的磁感应线(1)任何两条磁感应线不会相交。任何两条磁感应线不会相交。 (2)磁感应线是无头无尾的磁感应线是无头无尾的闭合曲线闭合曲线。（或两端伸向无穷远处）。（或两端伸向无穷远处）。 (3)磁感应线与电流之间互相套连，（即每条磁感磁感应线与电流之间互相套连，（即每条磁感应线都围绕着载流导线），两者服从右手螺旋定则，应线都围绕着载流导线），两者服从右手螺旋定则，即：即：ibib或：或： 磁感应线有以下特点磁感应线有以下特点:二、磁通量二、磁通

10、量 磁场的高斯定理磁场的高斯定理磁通量磁通量：通过磁场中某一曲面的磁感：通过磁场中某一曲面的磁感线数目叫做通过该曲面的磁通量。线数目叫做通过该曲面的磁通量。dsdnb1) 通过通过 面元的磁通量：面元的磁通量：sd bdsdmbdscossdbne为面元法线方向单位矢量。为面元法线方向单位矢量。nedssd称为称为面元矢量面元矢量。sdbsd2) 穿过某一曲面的磁通量：穿过某一曲面的磁通量：bsdbs2) 穿过某一曲面的磁通量：穿过某一曲面的磁通量：smmdssdbsbds cossmsbdbs0dd111sb0dd222sb0ssdb2ds22b3)穿过闭合曲面的磁通量穿过闭合曲面的磁通量:

11、smmdssdb规定：规定：取闭合曲面取闭合曲面外法线方向外法线方向为正向。为正向。磁力线穿出闭合面为正通量，磁力线穿出闭合面为正通量，磁力线穿入闭合面为负通量。磁力线穿入闭合面为负通量。（磁场的高斯定理）（磁场的高斯定理） 1ds11b物理意义物理意义：通过任意闭合曲面的磁通量：通过任意闭合曲面的磁通量 必等于零。必等于零。 磁场的高斯定理。磁场的高斯定理。0dsbs磁场是磁场是无源场无源场，磁感应线为，磁感应线为闭合曲线。闭合曲线。磁场中的高斯定理阐明了磁场的性质：磁场中的高斯定理阐明了磁场的性质： 由于磁感应线是闭合曲线，因此，通过任一闭由于磁感应线是闭合曲线，因此，通过任一闭合曲面磁通

12、量的代数和（净通量）必为零，亦即：合曲面磁通量的代数和（净通量）必为零，亦即：i1d2dlxobxdx例：例：如图载流长直导线的电流为如图载流长直导线的电流为 i ， 试求：试求：通过矩形面积的磁通量。通过矩形面积的磁通量。xib20sb/xlxisbd2dd021d2d0ddsxxl isb120ln2ddli 解：解：先求先求 ，对变磁场给出，对变磁场给出 后，积分求后，积分求db例：例：在匀强磁场在匀强磁场b中，有一半径为中，有一半径为r 的半球面的半球面s，s 边线边线所在平面的法线方向的单位矢量所在平面的法线方向的单位矢量 和和 b 的夹角为的夹角为 ，则：则：通过半球面通过半球面

13、s 的磁通量为：的磁通量为： 。nebsmcos解：解：将半球面和圆面组成将半球面和圆面组成一个闭合面，则一个闭合面，则通过此闭通过此闭合面的磁通量为零合面的磁通量为零。- b r2cos 即：通过半球面和即：通过半球面和通过圆面的磁通量数值通过圆面的磁通量数值相等而符号相反。相等而符号相反。b2r cos ne于是于是通过半球面的磁通量通过半球面的磁通量就可以通过圆面来计算就可以通过圆面来计算：sbmisji)23(s3 021 ss 021 )rb(s 21rbs 2）在均匀磁场在均匀磁场jib23 中，过中，过yoz平面内平面内面积为面积为s的磁通量。的磁通量。xoyzsnbro1s2s

14、b1）求均匀磁场中半求均匀磁场中半球面的磁通量。球面的磁通量。课课堂堂练练习习10.3 10.3 毕奥毕奥萨伐尔定律萨伐尔定律 1820年，法国科学家毕奥、萨伐尔和拉普年，法国科学家毕奥、萨伐尔和拉普拉斯在实验基础上，分析总结出拉斯在实验基础上，分析总结出电流元电流元产生磁产生磁场的规律：场的规律：毕奥毕奥萨伐尔定律萨伐尔定律。静电场静电场:qdedeed磁磁 场：场：lidbdbbd?lid电流元电流元 idl方向：方向：线元上通过的电流的方向。线元上通过的电流的方向。大小：大小：lid电流元电流元 iip*一、毕奥一、毕奥萨伐尔定律萨伐尔定律20sind4drlib 30d4drrlibl

15、idbd30d4drrlibb 任意载流导线在点任意载流导线在点 p 处的磁感强度处的磁感强度磁感强度叠加原理磁感强度叠加原理rlidrbd真空磁导率真空磁导率 270an104amt/1047说明：说明：30d4drrlib 1）该公式只适用于稳恒电流元；该公式只适用于稳恒电流元；4）毕奥毕奥萨伐尔定律是一个萨伐尔定律是一个实验定律实验定律，是由实验数，是由实验数据归纳得出。据归纳得出。 2）电流元在自身的方向上不激发磁场。电流元在自身的方向上不激发磁场。3）它是一个矢量积分，实际使用时，要化成标量它是一个矢量积分，实际使用时，要化成标量进行积分计算。进行积分计算。304rrlidbdb载流

16、导线载流导线 r 是从电流元是从电流元idl 指向场点指向场点 p 的矢量。的矢量。 r是电流元是电流元idl 到到 p 点的距离。点的距离。12345678lid例：例：判断下列各点磁感强度的方向和大小。判断下列各点磁感强度的方向和大小。r1、5 点点 ：0db3、7点点 ：204ddrlib02045sin4ddrlib2、4、6、8 点点 ：30d4drrlib二、二、毕奥毕奥-萨伐尔定律的应用萨伐尔定律的应用yxzipcdoabd解：解：20sind4drzib cdrzibb20sind4d sin/,cotarazaz2sin/dd 方向均沿方向均沿 x 轴的负方向轴的负方向bd1

17、221dsin40aib例：例：载流长直导线的磁场。载流长直导线的磁场。一段有限一段有限长载流直导线，通有电流为长载流直导线，通有电流为 i ，求：求：距直导线距直导线 a 处的处的 p 点的磁感应强度。点的磁感应强度。zzdryzipcdo12）（210coscos4ai 的方向沿的方向沿 x 轴的负方向。轴的负方向。b21dsin40aib）（210coscos4aib b（一段有限长载流直导线外的磁感应强度）（一段有限长载流直导线外的磁感应强度）1）无限长载流长直导线的磁场：）无限长载流长直导线的磁场：021rib20 ）（210coscos4aib 讨论：讨论：yzipcdo12ib

18、电流与磁感强电流与磁感强度成度成右螺旋关系右螺旋关系ib2）半无限长载流长直导线的磁场：）半无限长载流长直导线的磁场：ribp40ipr221）（210coscos4aib ,1 ;2 )1(cos40 aib3）半无限长载流直导线的磁场：）半无限长载流直导线的磁场：iap4）载流导线延长线上任一点的磁场）载流导线延长线上任一点的磁场:0 b,/ rlid0 rlid）（210coscos4aib iap例：例：一正方形载流线圈边长为一正方形载流线圈边长为 b，通有电流为，通有电流为 i，求：求：正方形中心的磁感应强度正方形中心的磁感应强度 b。iob解：解：o 点的点的 b 是由四条载流边分

19、别是由四条载流边分别产生的，它们大小相等、方向相同，产生的，它们大小相等、方向相同，b = b1+ b2+ b3+ b4= 4b1b21 ,41 432 43cos4cos2/440bibbi022210coscos4 aib求：求：边长为边长为 a 的正三角形中心的正三角形中心 o 点的磁场。点的磁场。riboo 4 电流电流 i 经三角形分流后，在经三角形分流后，在中心中心 o 点产生的磁场为零。点产生的磁场为零。 cd段在三角形中心段在三角形中心o点产点产生的磁场也为零。生的磁场也为零。 只有只有ab段在三角形中心段在三角形中心 o点产生磁场：点产生磁场：aiboo 43 3ar iab

20、oraicdi 分割电流元为无限多个、分割电流元为无限多个、宽为宽为 dx 的无限长载流直导线。的无限长载流直导线。解：解：建立坐标如图。建立坐标如图。电流元电流：电流元电流：apboxxdxaidi di例：例：一宽为一宽为 a 无限长载流平面，通有电无限长载流平面，通有电流流 i ，距平面左侧为距平面左侧为 b 与电流共与电流共面的面的 p 点磁感应强度点磁感应强度 b 的大小。的大小。xdidb20axidx20dbbbabaxidx 20bbaailn20dxix例：例：圆形载流导线轴线上的磁场。圆形载流导线轴线上的磁场。真空中，半径真空中，半径为为 r 的载流导线，通有电流的载流导线

21、，通有电流 i， 称圆电流。称圆电流。其轴线上一点其轴线上一点 p 的磁感强度的方向和大小。的磁感强度的方向和大小。 解：解：根据对称性分析根据对称性分析sindbbbx20d4drlibrbdbblidpro*xxrp*20cos4rldibdx lrldib20cos4 222cosxrrrr rlrirb2030d4 2322202）（rxirb 204rldibd obdrlid2322202）（rxirb rib20 3）0 x32032022xrixirb 4）rx2） 的方向不变的方向不变 ( 和和 成成右螺旋右螺旋关系）关系）0 xbib1）若线圈有若线圈有 匝匝n232220

22、2）（rxirnb 讨讨论论x*bxoriis载流线圈磁矩载流线圈磁矩nispmnxpbm302 ,230 xpbm 圆电流磁感应强度也可写成圆电流磁感应强度也可写成:3032022xisbxirb，4）rxmpmpisnnnispm对任意形状的载流线圈都适用：对任意形状的载流线圈都适用：载流线圈磁矩载流线圈磁矩04ibr 00244iibrr 08ibr例：例：直电流和圆电流的组合。直电流和圆电流的组合。求：求：圆心圆心 o 点的磁感应强度。点的磁感应强度。解：解：oiroriori例：例：直电流和圆电流的组合。直电流和圆电流的组合。求：求：圆心圆心 o 处的磁感应强度。处的磁感应强度。ri

23、boo4 rio4 rio 4 方向：方向：垂直纸面向里。垂直纸面向里。boriiacdibefrrocdia432 rio rio 4 bo=方向：方向：垂直纸面向外。垂直纸面向外。iro（1）x0boi2r1r（5）* ad（4）*o（2r）i+r（3）oirib200 rib400 rib800 1010200444riririb diba40 解：解：直线段直线段ab在在o点产生的磁场：点产生的磁场：030)6cos0(cos30sin4001rib)231(20ri方向向里方向向里cd段：段：)cos65(cos30sin4003rib)231(20ri产生的磁场产生的磁场圆弧圆弧

24、cb方向方向向里向里321bbbbriri6)231(00 例：例： 一根无限长导线一根无限长导线通有电流通有电流 i，中部弯成，中部弯成圆弧形。圆弧形。求：求：圆心圆心o点点的磁感应强度的磁感应强度b。roiiabcd0120ririb6312002例：例：计算组合载流导体在计算组合载流导体在 o 点的磁感应强度。点的磁感应强度。解：解：o 点点 b 由三段载流导体产生。由三段载流导体产生。cdbcabobbbb规定向里为正向，规定向里为正向，bcabobbbriri4400ri1140rabcd+ + + + + + + +pr+ +*例：例：载流直螺线管的磁场载流直螺线管的磁场 如图所示，有一长为如图所示，有一长为l , 半径为半径为r的载流密绕直螺的载流密绕直螺线管，螺线管的总匝数为线管，螺线管的总匝数为n，通有电流，通有电流i. 设把螺线管设把螺线管放在真空中，求管内轴线上一点处的磁感强度放在真空中，求管内轴线上一点处的磁感强度.2/322202）（rxirb解解 由圆形电流磁场公式由圆形电流磁场公式oxxdxop1xx2x+ + + + +