【高中数学必修二】柱、锥、台的表面积与体积（课堂PPT）

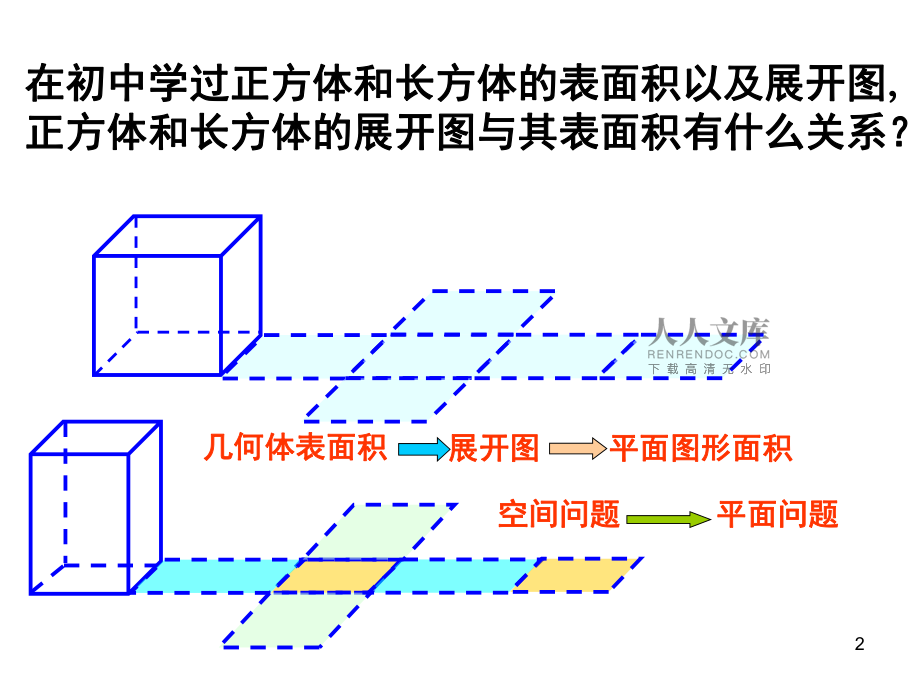
1、12在初中学过正方体和长方体的表面积以及展开图在初中学过正方体和长方体的表面积以及展开图, ,正方体和长方体的展开图与其表面积有什么关系？正方体和长方体的展开图与其表面积有什么关系？几何体表面积几何体表面积 展开图展开图 平面图形面积平面图形面积 空间问题空间问题 平面问题平面问题 3 正方体、长方体是由多个平面围成的几何体，它正方体、长方体是由多个平面围成的几何体，它们的们的表面积就是各个面的面积和表面积就是各个面的面积和 因此，我们可以把它们展成平面图形，利用平面因此，我们可以把它们展成平面图形，利用平面图形求面积的方法，求立体图形的表面积图形求面积的方法，求立体图形的表面积 棱柱、棱锥、

2、棱台都是由多个平面图形围成的几何棱柱、棱锥、棱台都是由多个平面图形围成的几何体，依据上述方法如何计算它们的表面积？体，依据上述方法如何计算它们的表面积？4h直棱柱的侧面展开图直棱柱的侧面展开图chS直棱柱侧S表表=S底底+S侧侧5正棱锥的侧面展开图正棱锥的侧面展开图侧面展开21chS正棱锥侧正棱锥侧S表表=S底底+S侧侧hh6正棱台的侧面展开图正棱台的侧面展开图侧面展开S表表=S底底+S侧侧hh) 21hccS （正正棱棱台台侧侧7棱柱、棱锥、棱台都是由多个平面图形围成的棱柱、棱锥、棱台都是由多个平面图形围成的多面体多面体，它们的侧面展开图还是平面图形，它，它们的侧面展开图还是平面图形，它们的

3、们的表面积就是各个侧面面积与底面面积之表面积就是各个侧面面积与底面面积之和和hS表表=S底底+S侧侧8底面积为底面积为_, 侧面积为侧面积为_,表面积为表面积为_.SBCA8234a23 34a23aSABC ,则它的则它的的三棱锥的三棱锥例例1:已知棱长为已知棱长为 , 各面均为等边三角形各面均为等边三角形a9圆柱的侧面展开图是矩形圆柱的侧面展开图是矩形2222()Srrlr rlOOrl2 r lSSr2 长长方方形形圆圆柱柱侧侧 圆柱、圆锥、圆台的展开图及表面积的求法：圆柱、圆锥、圆台的展开图及表面积的求法：10圆锥的侧面展开图是扇形圆锥的侧面展开图是扇形r2lOr2()Srrlr rl

4、rlS圆锥侧11r2lOrO r2 r圆台的侧面展开图是扇环圆台的侧面展开图是扇环22()Srrrlrl lrrSS)/（扇环圆台侧12lOrO rlOOrlOr2222()Srrlr rl 2()Srrlr rl22()Srrrlrl 圆柱、圆锥、圆台的表面积公式之间有什么关系？圆柱、圆锥、圆台的表面积公式之间有什么关系？上底扩大上底扩大上底缩小上底缩小r/=0r/=r13 例例2 2 如图，一个圆台形花盆盆口直径如图，一个圆台形花盆盆口直径20 cm20 cm，盆，盆底直径为底直径为15cm15cm，底部渗水圆孔直径为，底部渗水圆孔直径为1.5 cm1.5 cm，盆壁长，盆壁长15cm15

5、cm那么花盆的表面积约是多少平方厘米（那么花盆的表面积约是多少平方厘米（ 取取3.143.14，结果精确到，结果精确到1 1 ）？）？2cmcm15cm20cm15 解：由圆台的表面积公式得解：由圆台的表面积公式得 花盆的表面积：花盆的表面积：2225 . 11522015215215S)(9992cm答：花盆的表面积约是答：花盆的表面积约是999 999 2cm14练习：看图回答问题练习：看图回答问题_SS 圆圆锥锥侧侧圆圆锥锥表表_SS圆圆台台侧侧圆圆台台表表_SS 圆圆柱柱侧侧圆圆柱柱表表246311615柱体、锥体、台体的表面积柱体、锥体、台体的表面积各面面积之和各面面积之和rr0 r

6、展开图展开图)(22rllrrrS 圆台圆台圆柱圆柱)(2lrrS)(lrrS圆锥圆锥1617ShV 其中其中S为底面面积，为底面面积，h为棱柱的高为棱柱的高18ShV31(其中其中S为底面面积，为底面面积，h为高为高)19由于圆台由于圆台( (棱台棱台) )是由圆锥是由圆锥( (棱锥棱锥) )截成的，因此可以利用两个锥截成的，因此可以利用两个锥体的体积差得到圆台体的体积差得到圆台( (棱台棱台) )的体积公式的体积公式( (过程略过程略) )根据台体的特征，如何求台体的体积？根据台体的特征，如何求台体的体积？ABABCDCDPSShDCBAPABCDPVVVhSSSS)(3120台体（棱台、

7、圆台）的体积公式台体（棱台、圆台）的体积公式: :hSSSSV)(31 其中其中 ， 分别为上、下底面面积，分别为上、下底面面积，h为圆台为圆台（棱台）的高（棱台）的高SS21hSSSSV)(31S为底面面积，为底面面积，h为柱体高为柱体高ShV 0SS分别为上、下分别为上、下底面底面面积，面积，h 为台体高为台体高ShV31SS S为底面面积，为底面面积，h为锥体高为锥体高上底扩大上底扩大上底缩小上底缩小柱体、锥体、台体的体积公式之间有什么柱体、锥体、台体的体积公式之间有什么关系？关系？22 例例3 有一堆规格相同的铁制（铁的密度是有一堆规格相同的铁制（铁的密度是 ）六角螺帽共重）六角螺帽共

8、重5.8kg，已知底面是正六边，已知底面是正六边形，边长为形，边长为12mm，内孔直径为，内孔直径为10mm，高为，高为10mm，问这堆螺帽大约有多少个（问这堆螺帽大约有多少个（ 取取3.14）？）？3/8 . 7cmg 解：六角螺帽的体积是六棱柱解：六角螺帽的体积是六棱柱的体积与圆柱体积之差，即的体积与圆柱体积之差，即: :10)210(14. 3106124322V)(29563mm)(956. 23cm所以螺帽的个数为所以螺帽的个数为252)956. 28 . 7(10008 . 5（个）（个）答：这堆螺帽大约有答：这堆螺帽大约有252252个个23334RVR 的的球球的的体体积积为为

9、：定定理理：半半径径是是24 RSR的球的表面积为：定理：半径是24(1)(1)若球的表面积变为原来的若球的表面积变为原来的2 2倍倍, ,则半径变为原来的则半径变为原来的 倍倍. .(2)(2)若球半径变为原来的若球半径变为原来的2 2倍，则表面积变为原来的倍，则表面积变为原来的 倍倍. .(3)(3)若两球表面积之比为若两球表面积之比为1:21:2，则其体积之比是，则其体积之比是 . .(4)(4)若两球体积之比是若两球体积之比是1:21:2，则其表面积之比是，则其表面积之比是 . .2422:134:1 影响球的表面积及体积的只有一个元素，影响球的表面积及体积的只有一个元素，就是就是球的半径球的半径. . 25例例4 4：圆柱的底面直径与高都等于球的直径：圆柱的底面直径与高都等于球的直径