(完整word版)圆的知识点总结和典型例题,推荐文档

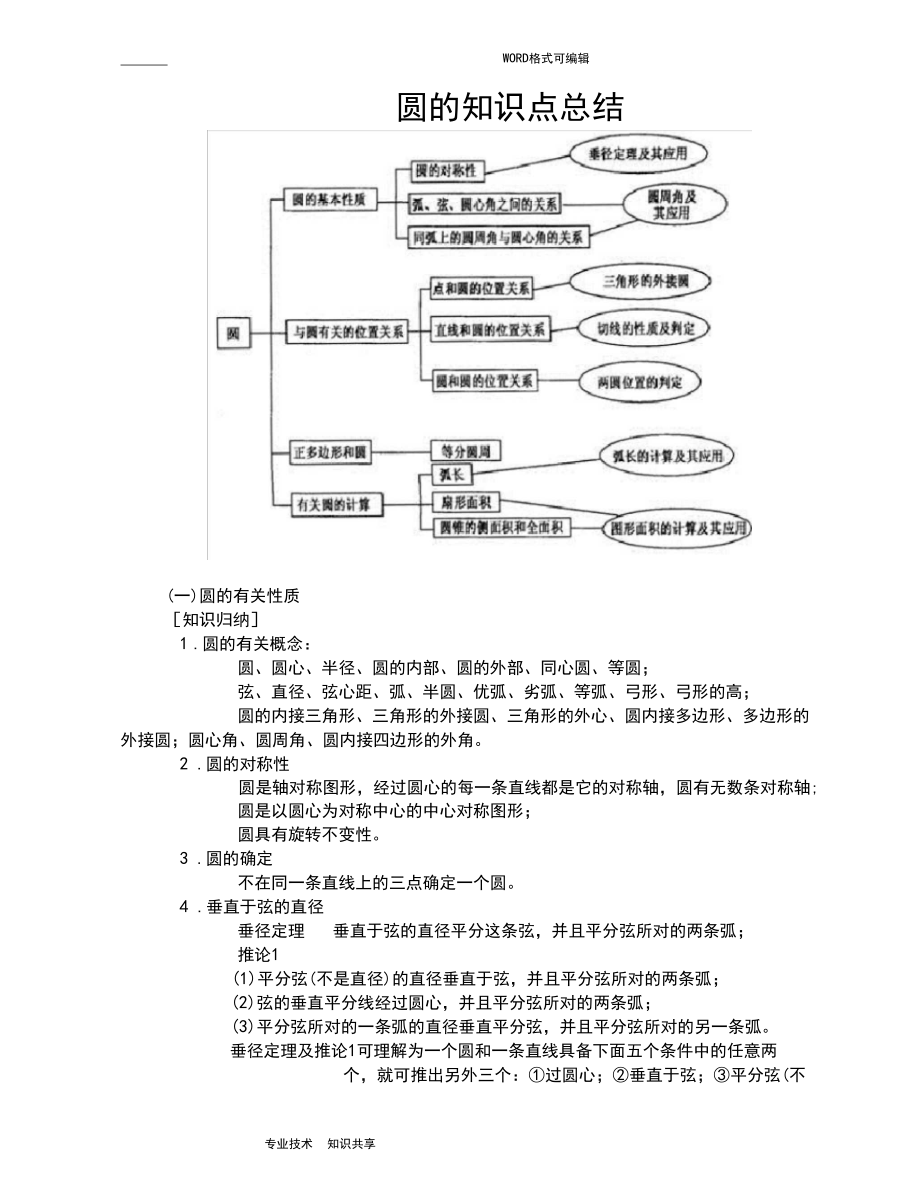
1、WORD格式可编辑圆的知识点总结(一)圆的有关性质知识归纳1 .圆的有关概念：圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高；圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆；圆心角、圆周角、圆内接四边形的外角。2 .圆的对称性圆是轴对称图形，经过圆心的每一条直线都是它的对称轴，圆有无数条对称轴; 圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性。3 .圆的确定不在同一条直线上的三点确定一个圆。4 .垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧；推论1(1)平分弦(不是直径)

2、的直径垂直于弦，并且平分弦所对的两条弧；(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧；(3)平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。垂径定理及推论1可理解为一个圆和一条直线具备下面五个条件中的任意两 个，就可推出另外三个：过圆心；垂直于弦；平分弦(不 是直径)；平分弦所对的优弧；平分弦所对的劣弧。推论2 圆的两条平行弦所夹的弧相等。5 .圆心角、弧、弦、弦心距之间的关系定理 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等；所对 的弦的弦心距相等。推论 在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心 距中有一组量相等，那么它们所对应的其余各组量

3、都分别相等。此定理和推论可以理解成：在同圆或等圆中，满足下面四个条件中的任何一个 就能推出另外三个：两个圆心角相等；两个圆心角所对的弧相等；两 个圆心角或两条弧所对的弦相等；两条弦的弦心距相等。圆心角的度数等于它所对的弧的度数。6 .圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半；推论1 同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对 的弧也相等；推论2 半圆(或直径)所对的圆周角是直角；90。的圆周角所对的弦是直径;推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三 角形。圆周角的度数等于它所对的弧的度数的一半。7 .圆内接四边形的性质圆内接四边形的对角

4、互补，并且任何一个外角都等于它的内对角。X8.轨迹轨迹 符合某一条件的所有的点组成的图形，叫做符合这个条件的点的轨迹。(1)平面内，到一定点的距离等于定长的点的轨迹，是以这个定点为圆心，定长为半径 的圆；(2)平面内，和已知线段两个端点的距离相等的点的轨迹，是这条线段的垂直平分线；(3)平面内，到已知角两边的距离相等的点的轨迹，是这个角的平分线。例题分析图1在。O中，半径OML弓gAB于点No专业技术知识共享2、后，ON= 1,求MN勺长;2指,半径OML AB,AN= BN= 若半径OM= R, / AO由120 ,求 MN勺长。.ONk 1,由勾股定理得OA= 2MN= OMk ON= O

5、A- O+ 1.半径 OML AB,且/ AO由 120. . / AOM 60-Rv ONh OA cosZ AON= OM cos60 = 2版M二 O-OM=22说明：如图 1, 一般地，若/ AO由2n , OMLAB于 N, A氏R, O*h, WJ AB=2依了, MN = R-h Sm = 2Rsin n 0 = 2htan n =180例2.已知：如图2,在AABC中，/ACB=90 , / B=25 ,以点C为圆心、AC为分析：因为弧与垂径定理有关；与圆心角、圆周角有关；与弦、弦心距有关；弧与弧之 间还存在着和、差、倍、半的关系，因此这道题有很多解法，仅选几种供参考。n解法一

6、：（用垂径定理求）如图 21,过点C作CH AB于点E,交。于点F。图21n c又/AC氏 900 , / B= 25 ,FCA= 25nri”的度数为25 ,为门的度数为50。解法二：（用圆周角求）如图 2 2,延长AC交。C于点E,连结ED图22. AE是直径， ./ ADE= 900. /AC四 90 , / B= 25 ,口的度数为50。解法三：（用圆心角求）如图.E= / B= 252 3,连结CD图23/ A= 65. /AC四 90 , / B= 25 ,. CA= CD ./AD。/A= 650 c丁/AC氏50 ,月日的度数为50例3.已知：如图3, ABC内接于。且AB=

7、AC,。的半径等于6cm, O点至U BC的距 离O*于2cm,求AB的长。析：因为不知道/ A是锐角还是钝角，因此圆心有可能在三角形内部，还可能在三角形 外部，所以需分两种情况进行讨论。略解：（1）假若/ A是锐角， ABCg锐角三角形。如图3,由A况AC可知点A是优 n弧的中点，因为ODL BC且AB= AC根据垂径定理推论可知，DOW延长线必过点A,连结 BO,. BO 6, OD= 2.BD - 8= 4 二 4&在 RtADB中，AA DOEAO=6+2= 8AB =通= +（3 = 4 网网图3- 1(2)若/A是钝角，则 ABC是钝角三角形，如图31添加辅助线及求出 的二4页，在

8、 RtzXADB中，AD= AO-D氏62 = 4.AB= WE = # + (4历=岛河综上所述AB=4派溺的 辰布小结：凡是与三角形外接圆有关的问题，一定要首先判断三角形的形状，确定圆心与三 角形的位置关系，防止丢解或多解。例4.已知：如图4, AB是。的直径，弦CDLAB, F是CD延长线上一点，AF交。O 于 E。求证：AE- EF= EC- ED图4分析：求证的等积式 AE- EF= EC- ED中，有两条线段EF、ED在4EDF中，另两条线段 AE、EC没有在同一三角形中，欲将其置于三角形中，只要添加辅助线AC设法证明 FE必 CEAW。证明：连结AC四边形DEACJ接于圆丁. /

9、 FDE= / CAE / FED= / DCA.直径 AB，CDq丁 / DCAf / CEA / FE5 / CEA .FED ACEADE _ EFAS EC , AE - EF= EC- ED小结：四边形内接于圆这一条件，常常不是在已知条件中明确给出的，而是隐含在图形 之中，在分析已知条件时，千万不要忽略这一重要条件。例5.已知：如图5, AM是。的直径，过。O上一点B作BN!AM垂足为N,其延长线 交。O于点C,弓C CD交AM于点E。图5(1)如果 CD1AB,求证：EN= NM(2)如果弦CD交AB于点F,且C5AB,求证CE= EF - ED;(3)如果弦CD绕点C旋转，并且与

10、AB的延长线交于点F,且CD= AB,那么(2)的结 论是否仍成立？若成立，请证明；若不成立，请说明理由。证明：(1)连结BM(如图51)图5-1. AM是直径， / ABMk 900,. CDL AB, . BM/ CD ./ECN= /MBN 又 AML BC . . CN= BN, RtACEINRtABMN-4= NM(2)连结 BD BE, AC (如图 5- 2)点E是BC垂直平分线 AM一点，.二B已EC n n n n.CD= AB, .CD= AB OD 二 BC丁 / AC氏 / BDC 又 AB= AC AE= AE. .AB草 MCE ；/ABE= /AC& /BDC

11、/BED公共角，. BE/AFEB .Bt=EF ER. CE= EF - ED(3)结论成立。如图5-3图5 3证明：仿（2）可证4AB草AACE .BE= CE 且/ABE= /ACE ri c又. AB= CD . . AB = 5 /AC乐 / DBC. BD/ AC ./ BDE Z ACE= 180而 / FB日 /AB巳 180丁. / BDE= / FBE 而/ BED公共角 .BED AFEB .BS=EF EdCE= EF- ED(二)直线与圆的关系1 .直线与圆的位置关系直线和圆的位置相离相切相父公共点的个数012公共点名称无切点交点直线名称无切线割线圆心到直线的 距离d

12、与半径r的 关系d rH =z|d2 .切线的判定经过半径的外端并且垂直于这条半径的直线是圆的切线。3 .切线的性质(1)圆的切线垂直于经过切点的半径；(2)推论1 经过圆心且垂直于切线的直线必经过切点；(3)推论2 经过切点且垂直于切线的直线必经过圆心。此定理及推论可理解为以下三个条件中任知其中两个就可推出第三个：垂直于切线；经过切点；经过圆心。4 .切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线 的夹角。5 .弦切角定理(1)弦切角等于它所夹的弧对的圆周角；(2)推论 如果两个弦切角所夹的弧相等，那么这两个弦切角也相等；(3)弦切角的度数等于它所夹的弧

13、的度数的一半。6 .和圆有关的比例线段(1)相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等；(2)推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项；(3)切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项；(4)推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。7 .三角形的内切圆(1)有关概念：三角形的内切圆、三角形的内心、圆的外切三角形、多边形的内切圆、 圆的外切多边形；(2)作图：作一个圆，使它和已知三角形的各边都相切。例题分析例6.已知：如图6, AB是。的直径，C是AB延长线上一点，C

14、G切。于D, DH AB于 E。图6求证：/ CD乐/ EDB分析：由AB是。的直径，联想到直径的三个性质:图61图62图63(1)直径上的圆周角是直角。若连结 AD则得RtAABDn n n n(2)垂径定理。如图6 2,若延长DE交。于F,则可得DE= EF,工已二月F ；(3)过直径外端的切线与直径垂直。如图 63,若过B点作。O的切线BM则AB!BM 由CD是。的切线，联想到切线的三个性质：(1)过切点的半径垂直于切线。如图 61,若连结OD则ODLCD(2)弦切角等于它所夹的弧对的圆周角。若连结 AD则/ CD乐/A;(3)切割线定理。如图 6, CD= CB- CA由DEL AB于

15、E,联想到以下一些性质：(1) RtzXDEEfr两锐角互余，即/ ED济/ EB590 ;(2)垂径定理。如图6 2,只要延长DE交。于F,则可得到相等的线段，相等的弧；(3)构造与射影定理相关的基本图形。即连结 AD,则可彳#到 AD配直角三角形，DE是斜边上的高，又可得到两对相等的锐角，三个相似的三角形，还可运用射影定理、勾股定 理、面积公式等。证明：连结 AD如图6,AB是直径，./ AD氏90 。. Dn AB,ED乐 /A. CD 是。的切线，./ CD乐 /A, 二/CD乐 / EDB此例题还有许多证法，比如连结 OD如图61,利用切线的定义；又比如延长 DE交。O 于F,连结B

16、F,如图6- 2,利用垂径定理；还可以过点 B作。的切线交CD于点M,如图6 -3,利用切线长定理，等等，这诸多证法，读者不妨试证之。小结：此例题证明/ CD乐/EDB即证明BD是/CDE勺平分线，由此证明可以联想到 AD 也是/ GDE勺平分线。另外，通过对此例题的分析和证明可知，图 64中隐含着很多图形的性质，如相等的锐 角、相等的线段、相等的弧及相似三角形等等，为此可将图 6- 4分解成三个基本图形。如图 65,以利于进一步理解线段之间的比例关系。图6-45=眈-BCkC=C * OC的此 项且D总寸E - AEAC - BC=CE。八 K二呢,林图6-5例7.已知：如图7,点P是半圆O

17、的直径BA延长线上的点，PC切半圆于C点，CDLAB 于 D点，若 PA PO 1: 2, D及4,求 tan/PCAR PC的长证明：连结CB.PC切半圆O于C点，PC与/B./P= / P,PA(C APCB.AC: BO PA PCtan ZLPCA = tan B =BC PC 2.AB是半圆O的直径，./ AC比90AD- An AD .八 AC2 口- 1-=，AD =-* BD = -SC, BD AB BD4又 ; CDL ABX4 = 1.AB= AN DB= 5.PC- PA* FB、= E4（皿+5出二2,二产C二28二史33,/A的平分线交BC于点D, E为AB例8.已

18、知：如图8,在RtABC中，/B= 90上的一点，D DC以D为圆心,DB长为半彳作。a图8求证：(1) AC是。D的切线；(2) AB+ EB= AC分析：(1)欲证AC与。D相切，只要证圆心 D到AC的距离等于。D的半径BQ因此 要作DF, AC于F(2)只要证AO AF+ FO AB+ EB,证明的关键是证 BE= FC,这又转化为证 EBD CFD 证明：(1)如图8,过D作DF!AC, F为垂足. AD是 / BAC的平分线，DBL AB, D及 DF点D到AC的距离等于圆D的半径.AC是。D的切线(2) v ABBD OD的半径等于 BD.AB 是。D 的切线，. AB= AF .

19、在 RtBED和 RtFCD, ED= CD BD= FD .BED AFCtD a BE= FC.AB+ BE= AF+ FO AC小结：有关切线的判定，主要有两个类型，若要判定的直线与已知圆有公共点，可采 用“连半径证垂直”的方法；若要判定的直线与已知圆的公共点没有给出，可采用“过圆心 作垂线，证垂线段等于半径”的方法。此例题属于后一类例9.已知：如图9, AB为。O的弦，P为BA延长线上一点，PE与。相切于点E, C n为月8中点，连CE交AB于点F。图9求证：一；分析：由已知可得 PE2= PAPB,因此要证PP = PAPB,只要证PE= PF。即证/ PFE =/ PEE证明一：如

20、图9,作直径CD交AB于点G,连结ED / CE氏 90 n .点C为且的中点，CD!AB,./CFG/D PE为。O切线，E为切点 /PE已 / D,/PE已 /CFG. /CFG /PFE ./PFE= / PEF a PE= PF. Pt=PA PB,. PP= PA- PB证明二：如图91,连结AC AE图9- 1cn n丁点C是川口的中点，月. / CA氏/AEC.PE切。O于点 E,./ PEA= /CvZ PFE= / CA拼 / C, / PEF= / PEA / AEC ./ PFE= / PEF. PE= PF. Pt=PA PB,. PP= PA- PB例10.(1)如图

21、10,已知直线AB过圆心O,交。于A、B,直线AF交。于F (不与B重合)，直线l交。于G D,交BA延长线于E,且与AF垂直，垂足为G,连结AC AD图10图 10-1求证：/ BA氏/CAG AC AD= AE AF(2)在问题(1)中，当直线l向上平行移动，与。O相切时，其它条件不变请你在图10-1中画出变化后的图形，并对照图10标记字母；问题(1)中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由证明：(1)连结BD.AB是。的直径，AD由900 AG口 / AD氏 900又: ACDB!。内接四边形丁. / AC8 / B, / BA氏 / CAG连结CF / BA氏

22、 / CAG / EAG= / FAB丁. / DAE= / FAC又/ADC= /F, .AD曰AAFCAD _ AR, AC - AD= AE- AF(2)见图10-1两个结论都成立，证明如下：连结BC. AB 是直径， ./ ACB= 900 /AC乐 /AG於 900. GC切。于 C, ./ GCAf /ABC丁. / BAC= / CAG(即 / BA氏 / CAG连结CFvZ CA8 / BAC / GCF / GAC / GCa / CAE / ACF= / ACG / GFC / E= / ACG / CAE /AC曰 / E, .ACS AE(C丁 .AC = AE AF

23、(即 AC- AD= AE- AF)说明：本题通过变化图形的位置，考查了学生动手画图的能力，并通过探究式的提问 加强了对学生证明题的考查，这是当前热点的考题，希望引起大家的关注。例11.如图11, AB是。的直径，O O过AC的中点D, DELBC,垂足为E。图11(1)由这些条件，你能推出哪些正确结论？(要求，不再标注其它字母，找结论的过程 中所连辅助线不能出现在结论中，不写推理过程，写出4个结论即可)。(2)若/ABC直角，其他条件不变，除上述结论外，你还能推出哪些新的正确结论？ 并画出图形。分析：(1)若连结DO可证得DE是。的切线。若连结DB,由直径AB和点D是AC的中点，可得AB=

24、BC / A= / C等。而且DHBC于 点E,又由双垂图形，可得5 =c,3C,谴=枇;防等。(2)连结DO OB方法同上。答：下列结论可供选择，如图图 11 1(1)DE是。O的切线CD= CE- CB11-1AB= BC /A= /C DU= BE - CE / C+ / CDE= 90 田 + DE2 = CD2(2)C已BE DE= BE DE= CE DE/ AB CB是。O的切线DE = -A2 b /a= ZCDE= 45/C= ZCDE= 45CD _CE _ DEcB = cdCA印 CB 可 (11)/炉十元二工CD _CB(12)-1说明：本题是结论开放的探索性问题，答

25、案不唯一。寻找结论的关键是抓住命题的条件 及其特点(尤其是利用特殊几何图形的判定和性质)，在几何中诸如：相等关系、特殊图形、 两图形的关系等。(三)圆和圆的位置关系知识归纳1.基本概念(1)两圆外离、外切、相交、内切、内含的定义。(2)两圆的公切线、外公切线、内公切线、公切线长的定义(3)两圆的连心线、圆心距、公共弦。2.圆和圆的位置关系两圆的位置圆心距d与两圆的 半径R r的关系外公切 线条数内公 切线 条数公切线 条数外离d 氏+川224外切213相交202内切d = R - r (R r)101内含d r)0003.相交两圆的性质：相交两圆的连心线垂直平分两圆的公共弦4.相切两圆的性质：

26、如果两圆相切，那么切点一定在连心线上例题分析例12.已知两圆外切时，圆心距为10cm,两圆内切时，圆心距为4cm,求两圆半径的长。 解：设两圆的半径分别为 Rcmff口 r cm。依题意，得答：大圆的半径为7cm,小圆的半径为3cmi例13.已知：如图12,两圆相交于A、B,过点A的直线交两圆于C、D,过点B的直线 交两圆于E、F。图12求证：CE/ FQ分析：要证CE/ FD,可通过角的关系证平行，即只要证/ E= /BFD或证/ EC济/D = 180 ,若证/ E= /BFD只需将/ BFD转化成与。O有关的圆周角，或圆内接四边形的外 角，只要连结 AB即可；若要证/ ECDk / D=

27、 180 ,也需连结 AB,得/ EBA= / D, / EBAH /EC氏180 ,则也可得证。证明一：（用同位角证）连结 AB丁四边形 EBACft接于。O,，/BAD= /E又 :/BF5 /BAD / BFD= /E.CE/ FD证明二：（用同旁内角证）连结 AB四边形EBACft接于。O,. /C+ / B= 180 ,又B=/D,/ C+ / D- 180 , EC/ FD小结：两圆相交时，常添的辅助线是作两圆的公共弦。(四)正多边形和圆知识归纳1 .基本概念正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角 以及平面镶嵌等。2 .正多边形的判定与性质(1

28、)把圆分成或舞之马等价:依次连结各分点所得的多边形是这个圆的内接正n边形；经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。(2)任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。3 .正多边形的有关计算正n边形的半径和边心距把正 n边形分成2n个全等的直角三角形。如图16所示，设正n边形的中心角为口，半径为R,边长为明 ,边心距为rn,周长为0二(3)用4.与圆有关的计算(1)圆的周长C= 2就；(2)弧长 180 ;g/*L 1.(3)圆的面积3n雄；(4)扇形面积病厩一克0 一 2；(5)弓形面积小就一%出帽一口.口(如图16)5 .与圆有关的作图(1)

29、过不在同一条直线上的三点作圆；(2)作三角形的内切圆；(3)等分圆周(三、六、十二、四、八、五等分)，作正三角形、正四边形、正六边6 .圆柱和圆锥的侧面展开图（1）圆柱的侧面积：彳血=2同（：底面半径，h：圆柱高）（2）圆锥的侧面积：（L= 2冗R, R是圆锥母线长，r是底面半径）。总成, X丽的一 W60 （n为侧面展开图扇形的圆心角的度数，R为母线长）。例题分析例14.已知：如图17,在两个同心圆中，大圆的弦 AB与小圆相切于点C, AB的长为 12cnn,求两个圆所围成的环形面积。图17解：连结OC OB设大圆半径O氏R,小圆半径O谖r.AB与小圆相切于点C, a OCLAB,且AC= BC ,. AB= 12