《图形的相似》测试题课件

1、姓名 班级 成绩 新泰市刘杜镇中心学校九年级图形的相似测试题一选择题（每题3分）1如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（）A2：3B：C4：9D8：272如图，下列条件不能判定ADBABC的是（）AABD=ACBBADB=ABCCAB2=ADACD=3如图，D、E分别是ABC的边AB、BC上的点，DEAC，若SBDE：SCDE=1：3，则SDOE：SAOC的值为（） ABCD4如图：把ABC沿AB边平移到ABC的位置，它们的重叠部分（即图中阴影部分）的面积是ABC面积的一半，若AB=，则此三角形移动的距离AA是（）A1BC1D5如图，已知AB、CD、EF都与BD

2、垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（） ABCD6. ABCA1B1C1，且相似比为，A1B1C1A2B2C2，且相似比为，则ABC与A2B2C2的相似比为（）ABC或D7如图，A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，如果RPQABC，那么点R应是甲、乙、丙、丁四点中的（） A甲B乙C丙D丁8如图，ABC中，点D在线段BC上，且ABCDBA，则下列结论一定正确的是（）AAB2=BCBDBAB2=ACBDCABAD=BCBDDABDC=ADBC9在平面直角坐标系中，已知点A（4，2），B（6，4），以原点O为位似中心，相似比为，把ABO缩小，则点A的对

3、应点A的坐标是（）A（2，1）B（8，4）C（8，4）或（8，4）D（2，1）或（2，-1）10在平面直角坐标系中，已知点A（4，2），B（2，2），以原点O为位似中心，相似比为，把AOB缩小，则点A的对应点A的坐标是（）A（2，1）B（8，4）C（8，4）或（8，4）D（2，1）或（2，1）11如图，DEBC，SADE=S四边形BCED，则AD：AB的值是（） ABCD12如图，在ABC中，D、E分别是AB、AC上的点，且DEBC，如果AE：EC=1：4，那么SADE：SEBC=（）A1：24B1：20C1：18D1：1613如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动

4、时她测得一根长为1m的竹竿的影长是0.8m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），他先测得留在墙壁上的影高为1.2m，又测得地面的影长为2.6m，请你帮她算一下，树高是（） A3.25mB4.25mC4.45mD4.75m14下列说法错误的是（）A两个等边三角形一定相似B两个等腰三角形一定相似C两个等腰直角三角形一定相似D两个全等三角形一定相似15如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（）时，ABE与以D、M、N为顶点的三角形相似ABC或D或二填空题（每题3分）16将一副三角板按图叠

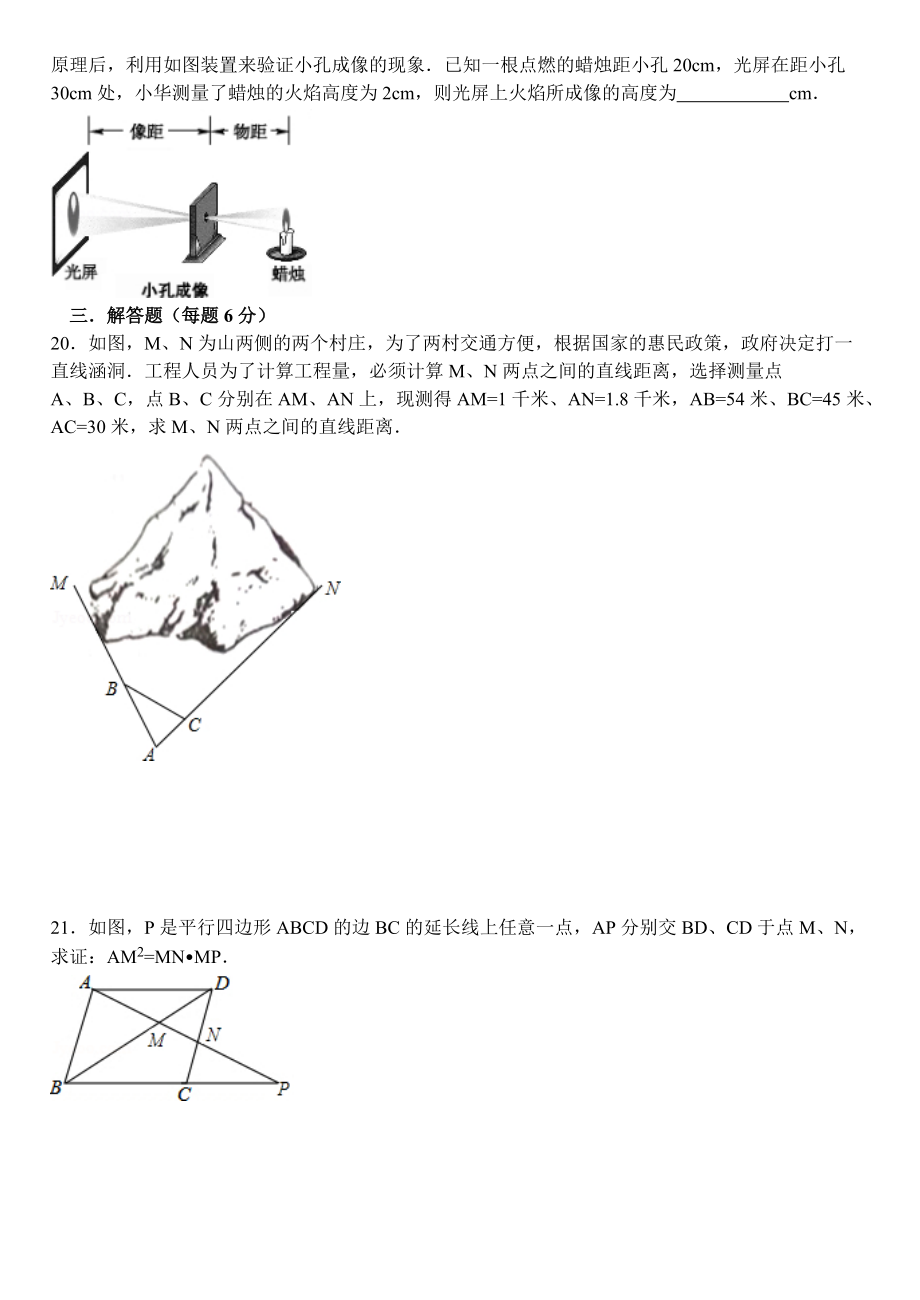
5、放，则AOB与DOC的面积之比等于 17如图，矩形EFGH内接于ABC，且边FG落在BC上若BC=3，AD=2，EF=EH，那么EH的长为18如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14cm，则楼高CD为m19两千多年前，我国的学者墨子和他的学生做了小孔成像的实验他的做法是，在一间黑暗的屋子里，一面墙上开一个小孔，小孔对面的墙上就会出现外面景物的倒像小华在学习了小孔成像的原理后，利用如图装置来验证小孔成像的现象已知一根点燃的蜡烛距小孔20cm，光屏在距小孔30cm处，小华测量了蜡烛的火焰高度为2cm，则光屏上火焰所成像的高度为cm三解答题（每题6分）20如

6、图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1.8千米，AB=54米、BC=45米、AC=30米，求M、N两点之间的直线距离21如图，P是平行四边形ABCD的边BC的延长线上任意一点，AP分别交BD、CD于点M、N，求证：AM2=MNMP22如图，矩形ABCD为台球桌面，AD=260cm，AB=130cm，球目前在E点位置，AE=60cm如果小丁瞄准BC边上的点F将球打过去，经过反弹后，球刚好弹到D点位置（1）求证：B

7、EFCDF；（2）求CF的长23在太阳光下，身高为1.6米的小芳在地面上的影长为2米当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子在墙上经测量，地面部分影长为8.5米，墙上影长为1.2米，那么这棵大树高约多少米？2015年09月21日ldyzal的初中数学组卷参考答案与试题解析一选择题（共15小题）1（2015贵阳）如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（）A2：3B：C4：9D8：27考点：相似三角形的性质菁优网版权所有分析：根据相似三角形的面积的比等于相似比的平方，据此即可求解解答：解：两个相似三角形面积的比是（2：3）2=4：9故选C点评：

8、本题考查对相似三角形性质的理解（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比2（2015永州）如图，下列条件不能判定ADBABC的是（）AABD=ACBBADB=ABCCAB2=ADACD=考点：相似三角形的判定菁优网版权所有分析：根据有两个角对应相等的三角形相似，以及根据两边对应成比例且夹角相等的两个三角形相似，分别判断得出即可解答：解：A、ABD=ACB，A=A，ABCADB，故此选项不合题意；B、ADB=ABC，A=A，ABCADB，故此选项不合题意；C、AB2=ADAC，=，A=A，A

9、BCADB，故此选项不合题意；D、=不能判定ADBABC，故此选项符合题意故选：D点评：本题考查了相似三角形的判定，利用了有两个角对应相等的三角形相似，两边对应成比例且夹角相等的两个三角形相似3（2015酒泉）如图，D、E分别是ABC的边AB、BC上的点，DEAC，若SBDE：SCDE=1：3，则SDOE：SAOC的值为（）ABCD考点：相似三角形的判定与性质菁优网版权所有分析：证明BE：EC=1：3，进而证明BE：BC=1：4；证明DOEAOC，得到=，借助相似三角形的性质即可解决问题解答：解：SBDE：SCDE=1：3，BE：EC=1：3；BE：BC=1：4；DEAC，DOEAOC，=，S

10、DOE：SAOC=，故选D点评：本题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答4（2015呼伦贝尔）如图：把ABC沿AB边平移到ABC的位置，它们的重叠部分（即图中阴影部分）的面积是ABC面积的一半，若AB=，则此三角形移动的距离AA是（）A1BC1D考点：相似三角形的判定与性质；平移的性质菁优网版权所有专题：压轴题分析：利用相似三角形面积的比等于相似比的平方先求出AB，再求AA就可以了解答：解：设BC与AC交于点E，由平移的性质知，ACACBEABCASBEA：SBCA=AB2：AB2=1：2AB=AB=1AA=ABAB

11、=1故选A点评：本题利用了相似三角形的判定和性质及平移的性质：平移不改变图形的形状和大小；经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等5（2015株洲）如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（）ABCD考点：相似三角形的判定与性质菁优网版权所有分析：易证DEFDAB，BEFBCD，根据相似三角形的性质可得=，=，从而可得+=+=1然后把AB=1，CD=3代入即可求出EF的值解答：解：AB、CD、EF都与BD垂直，ABCDEF，DEFDAB，BEFBCD，=，=，+=+=1AB=1，CD=3，+=1，EF=故选C

12、点评：本题主要考查的是相似三角形的判定与性质，发现+=1是解决本题的关键6（2015东光县校级二模）一个矩形剪去一个以宽为边长的正方形后，所剩下的矩形与原矩形相似，则原矩形的长与宽的比是（）ABCD考点：相似多边形的性质；解一元二次方程-公式法菁优网版权所有分析：利用相似多边形的相似比相等列出方程求解解答：解：设矩形的长是a，宽是b，则DE=CF=ab，矩形ABCD矩形CDEF，=，即=，整理得：a2abb2=0，两边同除以b2，得（）21=0，解得=或（舍去）故选D点评：根据相似得到方程，解方程是解决本题的关键7（2015石家庄模拟）如图，A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点

13、，如果RPQABC，那么点R应是甲、乙、丙、丁四点中的（）A甲B乙C丙D丁考点：相似三角形的性质菁优网版权所有专题：网格型分析：根据相似三角形的对应高的比等于相似比，代入数值即可求得结果解答：解：RPQABC，即，RPQ的高为6故点R应是甲、乙、丙、丁四点中的乙处故选B点评：此题考查了相似三角形的性质：相似三角形的对应高的比等于相似比解题的关键是数形结合思想的应用8（2015江都市一模）如图，ABC中，点D在线段BC上，且ABCDBA，则下列结论一定正确的是（）AAB2=BCBDBAB2=ACBDCABAD=BCBDDABAC=ADBC考点：相似三角形的性质菁优网版权所有分析：根据相似三角形的

14、对应边成比例进行判断，要注意相似三角形的对应边和对应角解答：解：ABCDBA，=；AB2=BCBD，ABAC=ADBC；故选AD点评：此题主要考查的是相似三角形的性质，正确地判断出相似三角形的对应边和对应角是解答此题的关键9（2015十堰）在平面直角坐标系中，已知点A（4，2），B（6，4），以原点O为位似中心，相似比为，把ABO缩小，则点A的对应点A的坐标是（）A（2，1）B（8，4）C（8，4）或（8，4）D（2，1）或（2，1）考点：位似变换；坐标与图形性质菁优网版权所有分析：根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或k，即可

15、求得答案解答：解：点A（4，2），B（6，4），以原点O为位似中心，相似比为，把ABO缩小，点A的对应点A的坐标是：（2，1）或（2，1）故选：D点评：此题考查了位似图形与坐标的关系此题比较简单，注意在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标比等于±k10（2015平定县一模）在平面直角坐标系中，已知点A（4，2），B（2，2），以原点O为位似中心，相似比为，把AOB缩小，则点A的对应点A的坐标是（）A（2，1）B（8，4）C（8，4）或（8，4）D（2，1）或（2，1）考点：位似变换；坐标与图形性质菁优网版权所有分析：直接利用位似图形的

16、性质得出对应点坐标乘以k或k进而求出即可解答：解：点A（4，2），B（2，2），以原点O为位似中心，相似比为，把AOB缩小，点A的对应点A的坐标是：（2，1）或（2，1）点评：此题主要考查了位似变换的性质以及坐标与图形的性质，正确记忆对应点坐标变化规律是解题关键11（2013秋蚌埠期中）如图，DEBC，SADE=S四边形BCED，则AD：AB的值是（）ABCD考点：相似三角形的性质菁优网版权所有分析：由DEBC，可得ADEABC，又由SADE=S四边形BCED，根据相似三角形的面积比等于相似比的平方，即可求得AD：AB的值解答：解：DEBC，ADEABC，SADE=S四边形BCED，SADE：

17、SABC=（AD：AB）2=1：2，AD：AB=故选：B点评：此题考查了相似三角形的判定与性质此题难度不大，解题的关键是注意相似三角形的面积比等于相似比的平方定理的应用与数形结合思想的应用12（2015徐汇区一模）如图，在ABC中，D、E分别是AB、AC上的点，且DEBC，如果AE：EC=1：4，那么SADE：SEBC=（）A1：24B1：20C1：18D1：16考点：相似三角形的判定与性质菁优网版权所有分析：由已知条件可求得，又由平行线分线段成比例可求得，结合SBDE=SABESADE可求得答案解答：解：=，=，SABE=SEBC，DEBC，=，=，SBDE=4SADE，又SBDE=SABE

18、SADE，4SADE=SEBCSADE，=，故选B点评：本题主要考查平行线分线段成比例的性质及三角形的面积，掌握同高三角形的面积比即为底的比是解题的关键13（2015聊城模拟）如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为1m的竹竿的影长是0.8m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），他先测得留在墙壁上的影高为1.2m，又测得地面的影长为2.6m，请你帮她算一下，树高是（）A3.25mB4.25mC4.45mD4.75m考点：相似三角形的应用菁优网版权所有分析：此题首先要知道在同一时刻任何物体的高与其影子

19、的比值是相同的，所以竹竿的高与其影子的比值和树高与其影子的比值相同，利用这个结论可以求出树高解答：解：如图，设BD是BC在地面的影子，树高为x，根据竹竿的高与其影子的比值和树高与其影子的比值相同得而CB=1.2，BD=0.96，树在地面的实际影子长是0.96+2.6=3.56，再竹竿的高与其影子的比值和树高与其影子的比值相同得，x=4.45，树高是4.45m故选C点评：解题的关键要知道竹竿的高与其影子的比值和树高与其影子的比值相同14（2015春乳山市期末）下列说法错误的是（）A两个等边三角形一定相似B两个等腰三角形一定相似C两个等腰直角三角形一定相似D两个全等三角形一定相似考点：相似三角形的

20、判定菁优网版权所有分析：根据等边三角形的性质和相似三角形的判定方法对A进行判断；利用反例对B进行判断；根据等腰直角三角形的性质和相似三角形的判定方法对C进行判断；根据全等三角形的性质和相似三角形的判定方法对D进行判断解答：解：A、两个等边三角形一定相似，所以A选项的说法正确；B、两个等腰三角形不一定相似，如等边三角形与等腰直角三角形不相似，所以B选项的说法错误；C、两个等腰直角三角形一定相似，所以C选项的说法正确；D、两个全边三角形一定相似，所以D选项的说法正确故选B点评：本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似15（2015春江津区校级月考）如图，正方形ABCD的边长为2

21、，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（）时，ABE与以D、M、N为顶点的三角形相似ABC或D或考点：相似三角形的判定；正方形的性质菁优网版权所有分析：根据AE=EB，ABE中，AB=2BE，所以在MNC中，分CM与AB和BE是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系，然后利用勾股定理列式计算即可解答：解：四边形ABCD是正方形，AB=BC，BE=CE，AB=2BE，又ABE与以D、M、N为顶点的三角形相似，DM与AB是对应边时，DM=2DNDM2+DN2=MN2=1DM2+DM2=1，解得DM=；DM与BE是对应边时，DM=DN，DM2+DN

22、2=MN2=1，即DM2+4DM2=1，解得DM=DM为或时，ABE与以D、M、N为顶点的三角形相似故选C点评：本题考查相似三角形的判定与性质、正方形的性质解决本题特别要考虑到DM与AB是对应边时，当DM与BE是对应边时这两种情况二填空题（共4小题）16（2015自贡）将一副三角板按图叠放，则AOB与DOC的面积之比等于1：3考点：相似三角形的判定与性质菁优网版权所有专题：压轴题分析：一副三角板按图叠放，则得到两个相似三角形，且相似比等于1：，相似三角形的性质相似三角形面积的比等于相似比的平方得到AOB与DOC的面积之比等于1：3解答：解：ABC=90°，DCB=90°AB

23、CD，OCD=A，D=ABO，AOBCOD又AB：CD=BC：CD=tan30°=1：AOB与DOC的面积之比等于1：3故答案为：1：3点评：本题考查对相似三角形性质的理解，相似三角形面积的比等于相似比的平方17（2015柳州）如图，矩形EFGH内接于ABC，且边FG落在BC上若BC=3，AD=2，EF=EH，那么EH的长为考点：相似三角形的判定与性质；矩形的性质菁优网版权所有专题：应用题；压轴题分析：设EH=3x，表示出EF，由ADEF表示出三角形AEH的边EH上的高，根据三角形AEH与三角形ABC相似，利用相似三角形对应边上的高之比等于相似比求出x的值，即为EH的长解答：解：四边

24、形EFGH是矩形，EHBC，AEHABC，AMEH，ADBC，=，设EH=3x，则有EF=2x，AM=ADEF=22x，=，解得：x=，则EH=故答案为：点评：此题考查了相似三角形的判定与性质，以及矩形的性质，熟练掌握相似三角形的判定与性质是解本题的关键18（2015吉林）如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14cm，则楼高CD为12m考点：相似三角形的应用菁优网版权所有专题：应用题分析：先根据题意得出ABEACD，再根据相似三角形的对应边成比例即可求出CD的值解答：解：EBAC，DCAC，EBDC，ABEACD，=，BE=1.5，AB=2，BC=14

25、，AC=16，=，CD=12故答案为：12点评：本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例的性质是解答此题的关键19（2015西城区二模）两千多年前，我国的学者墨子和他的学生做了小孔成像的实验他的做法是，在一间黑暗的屋子里，一面墙上开一个小孔，小孔对面的墙上就会出现外面景物的倒像小华在学习了小孔成像的原理后，利用如图装置来验证小孔成像的现象已知一根点燃的蜡烛距小孔20cm，光屏在距小孔30cm处，小华测量了蜡烛的火焰高度为2cm，则光屏上火焰所成像的高度为3cm考点：相似三角形的应用菁优网版权所有专题：跨学科分析：如图，OE=20cm，OF=30cm，AB=2cm，通过证明OA

26、BOCD得到=，然后利用比例性质求CD即可解答：解：如图，OE=20cm，OF=30cm，AB=2cm，ABCD，OABOCD，=，即=，CD=3（cm），即光屏上火焰所成像的高度为3cm点评：本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度（测量距离）；借助标杆或直尺测量物体的高度三解答题（共5小题）20（2015菏泽）（1）如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1.8千米，AB=54

27、米、BC=45米、AC=30米，求M、N两点之间的直线距离（2）列方程（组）或不等式（组）解应用题：2015年的5月20日是第15个中国学生营养日，我市某校社会实践小组在这天开展活动，调查快餐营养情况他们从食品安全监督部门获取了一份快餐的信息（如表） 信息1、快餐成分：蛋白质、脂肪、碳水化合物和其他2、快餐总质量为400克3、碳水化合物质量是蛋白质质量的4倍若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%，求这份快餐最多含有多少克的蛋白质？考点：相似三角形的应用；一元一次不等式的应用菁优网版权所有分析：（1）先根据相似三角形的判定得出ABC相似与AMN，再利用相似三角

28、形的性质解答即可；（2）设这份快餐含有x克的蛋白质，根据所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%，列出不等式，求解即可解答：解：（1）在ABC与AMN中，A=A，ABCAMN，即，解得：MN=1.5千米，答：M、N两点之间的直线距离是1.5千米；（2）设这份快餐含有x克的蛋白质，根据题意可得：x+4x400×70%，解不等式，得x56答：这份快餐最多含有56克的蛋白质点评：此题考查相似三角形和一元一次不等式的应用，关键是根据相似三角形的判定和性质解答问题，读懂题意，找出题目中的数量关系，列出不等式，本题的数量关系是所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%21（2015岳池县模拟）如图，P是平行四边形ABCD的边BC的延长线上任意一点，AP分别交BD、CD于点M、N，求证：AM2=MNMP考点：相似三角形的判定与性质；平行四边形的性质菁优网版权所有专题：证明题分析：可证明ABMNDM，MBPMDA，利用相似三角形的性质可证得结论解答：证明：四边形ABCD是平行四边形，ADBP，ABCD，ABMNDM，MBPMDA，=，=，=，AM2=MNMP点评：本题主要考查相似三角形的判定和性质，由平行四边形的性质证明三角形相似是解题的关键，化乘积