改232《双曲线的几何性质(2)》

1、焦点在焦点在x轴上的双曲线的几何性质轴上的双曲线的几何性质 双曲线标准方程：双曲线标准方程：YX12222 byax0 byax1、 范围：范围：xa或或x-a2、对称性：、对称性：关于关于x轴，轴，y轴，原点对称。轴，原点对称。3、顶点、顶点:A1（-a，0），），A2（a，0）4、轴：实轴、轴：实轴 A1A2 虚轴虚轴 B1B2A1A2B1B25、渐近线方程：、渐近线方程：6、离心率：、离心率： e=ac复习回顾：复习回顾：,ace 222bac 几几？四四个个参参数数中中，知知几几可可求求、在在ecba（1）等轴双曲线的离心率等轴双曲线的离心率e= ?2( 2 )的的双双曲曲线线是是等等

2、轴轴双双曲曲线线离离心心率率2e 知二求二知二求二. .思考：思考：焦点在焦点在y轴上的双曲线的几何性质口答轴上的双曲线的几何性质口答 双曲线标准方程：YX12222 bxayxbay 1、 范围：范围：ya或或y-a2、对称性：、对称性： 关于关于x轴，轴，y轴，原点对称。轴，原点对称。3、顶点：、顶点：B1（0，-a），），B2（0，a）4、轴：、轴： A1A2B1B25、渐近线方程：、渐近线方程：6、离心率：、离心率：e=c/aF2F2o实轴实轴 B1B2 ; 虚轴虚轴 A1A2小小 结结xyoax 或或ax ay ay 或或)0 ,( a ), 0(a xaby xbay ace)(2

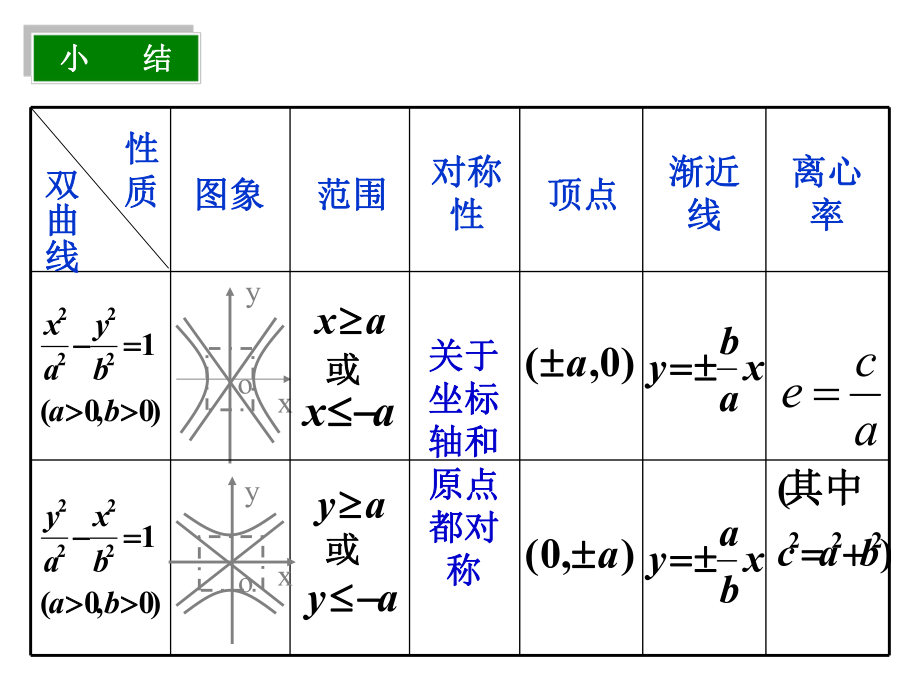
3、22bac 其其中中关于关于坐标坐标轴和轴和原点原点都对都对称称性性质质双曲线双曲线) 0, 0(12222 babyax) 0, 0(12222 babxay范围范围对称对称 性性 顶点顶点 渐近渐近 线线离心离心 率率图象图象 xyo渐近线渐近线离心率离心率顶点顶点对称性对称性范围范围|x| a,|y|b|x| a，y R对称轴：对称轴：x轴，轴，y轴轴 对称中心：原点对称中心：原点对称轴：对称轴：x轴，轴，y轴轴 对称中心：原点对称中心：原点（-a,0) (a,0) (0,b) (0,-b)长轴：长轴：2a 短轴：短轴：2b(-a,0) (a,0)实轴：实轴：2a虚轴：虚轴：2be =a

4、c( 0e 1 )ace=(e1)无无 y = abxyXF10F2MXY0F1F2 p图象图象1 1、填表、填表618|x|3(3,0) 0 ,103 10 ey=3x44|y|2(0,2)2 e 22, 0 xy 例已知双曲线的焦点在例已知双曲线的焦点在y轴上，焦距为轴上，焦距为16，离，离心率是心率是4/3，求双曲线的标准方程。并求其渐近线方程及求双曲线的标准方程。并求其渐近线方程及焦点坐标焦点坐标,162 c解解：由由题题意意得得. 8 c34 ac又又则则解解得得, 6 a.286822222 acb轴上轴上双曲线的焦点在双曲线的焦点在又又y. 1283622 xy为为所求双曲线的标

5、准方程所求双曲线的标准方程例例.求下列双曲线的渐近线方程，并画出图像：求下列双曲线的渐近线方程，并画出图像： 149).122 yx解：1) , 92 a42 b, 3 a2 b2)把方程化为标准方程把方程化为标准方程 19422 xy, 42 a92 b, 2 a3 bx32y 渐渐近近线线方方程程是是x.32y 渐渐近近线线方方程程是是149).222 yx0 xy如何记忆双曲线的渐进线方程？如何记忆双曲线的渐进线方程？14922 yx双曲线方程双曲线方程369422 yx双双曲曲线线方方程程. 44yx22双双曲曲线线方方程程. 4x4y22双双曲曲线线方方程程x32y 渐渐近近线线方方

6、程程是是x.32y 渐近线方程是渐近线方程是02 yx渐渐近近线线方方程程双曲线方程与其渐近线方程之间有什么规律双曲线方程与其渐近线方程之间有什么规律?. 023x y渐渐近近线线方方程程是是. 032 yx渐渐近近线线方方程程是是02 xy渐渐近近线线方方程程. 0, 0)122222222 byaxbyaxbyax即即的的渐渐近近线线方方程程是是双双曲曲线线 )0.(0)22222 byaxbyax的的双双曲曲线线方方程程是是渐渐近近线线方方程程为为02222byax0)(byaxbyax或0byax. 0byaxxaby02222yaxb0)(aybxaybx或0aybx0aybxxab

7、y能不能直接由双曲线方程得出它的渐近线方程？能不能直接由双曲线方程得出它的渐近线方程？结论：结论：oxy解：4,2)x21y4xM（的的交交于于与与渐渐近近线线点点作作直直线线过过Q32 ,xx21y轴轴上上在在的的下下方方，即即双双曲曲线线焦焦点点点点在在直直线线M1ba2222 yx设双曲线方程为设双曲线方程为得得到到入入上上式式代代），把把双双曲曲线线经经过过点点（,)3, 4(34,1, 4)2),122 ba解得解得由由例例4已知双曲线的渐近线是已知双曲线的渐近线是 ，并且双曲线过点，并且双曲线过点02 yx)3, 4(M求双曲线方程。求双曲线方程。Q4M1b)3(a42222 1)

8、x21y 渐近线是渐近线是又又21 ab2).44yx22双双曲曲线线方方程程为为例例4已知双曲线的渐近线是已知双曲线的渐近线是 ，并且，并且双曲线过点双曲线过点02 yx),3, 4(M求双曲线方程。求双曲线方程。.44yx22所所求求双双曲曲线线方方程程为为022 yx双曲线的渐近线方程为双曲线的渐近线方程为：解解.422 yx为为可设所求双曲线的方程可设所求双曲线的方程)3, 4(M双曲线过点双曲线过点.)3(4422 4 练习册练习册2222页例页例1 1小结：小结：. xaby1. 12222的渐近线是byax的渐近线是直线y1. 22222aybxxba. 0, 0. 322222

9、222byaxbyaxbyax即的渐近线方程是双曲线.0. 42222byaxbyax的双曲线方程是渐近线方程为知识要点：知识要点：技法要点：技法要点： 2、求与椭圆求与椭圆xy221681有共同焦点，渐近线方程为有共同焦点，渐近线方程为xy30的双曲线方程。的双曲线方程。 解：解：椭圆的焦点在椭圆的焦点在x轴上，且坐标为轴上，且坐标为），（，022)022(21FF 双曲线的焦点在 轴上，且xc2 2双曲线的渐近线方程为双曲线的渐近线方程为xy33 bacabab33822222，而， 解出解出2622ba， 双曲线方程为xy22621 .)2(;) 1 (.,3四个焦点在同一个圆上线的双曲

10、线的它的共轭双曲同的渐近线线有共双曲线和它的共轭双曲结论：线的共轭双曲线做原双曲实轴为虚轴的双曲线叫实轴以已知双曲线的虚轴为例F1F2F1/F2/yxO1、“共渐近线共渐近线”的双曲线的应的双曲线的应用用222222221(0)xyabxyab 与共渐近线的双曲线系方程为， 为参数 ，0表示焦点在表示焦点在x轴上的双曲线；轴上的双曲线；a0)，求点，求点M的轨迹的轨迹.cx2aacM解：解：设点设点M(x,y)到到l的距离为的距离为d，则，则|MFcda 即即222()xcycaaxc 化简得化简得(c2a2)x2 a2y2=a2 (c2 a2) 设设c2a2 =b2，22221xyab (a

11、0,b0)故点故点M的轨迹为实轴、虚轴长分别为的轨迹为实轴、虚轴长分别为2a、2b的双曲线的双曲线.222()|axcyacx 22224222(2)2axcxcyaa cxc x b2x2a2y2=a2b2即即就可化为就可化为:M点点M的轨迹也包括双的轨迹也包括双曲线的左支曲线的左支.一、第二定义一、第二定义 F1F2Oxyl/l Ml/ll/ll/ll/ll/l准准线线双曲线的第二定义双曲线的第二定义 平面内，若平面内，若定点定点F不在定直线不在定直线l上，则到定点上，则到定点F的的距离与到定直线距离与到定直线l的距离比为常数的距离比为常数e(e1)的点的轨迹是的点的轨迹是双曲线双曲线。

12、定点定点F是是双曲线的焦点双曲线的焦点，定直线叫做，定直线叫做双曲线双曲线的准线的准线，常数，常数e是是双曲线的离心率双曲线的离心率.对于双曲线对于双曲线22221xyab 是相应于右焦点是相应于右焦点F(c, 0)的的右准线右准线类似于椭圆类似于椭圆2axc 是相应于左焦点是相应于左焦点F(-c, 0)的的左准线左准线2axc xyoFlMF2axc l2axc 点点M到左焦点与左准线的距到左焦点与左准线的距离之比也满足第二定义离之比也满足第二定义.想一想：想一想：中心在原中心在原点，焦点在点，焦点在y轴上轴上的双曲线的准线的双曲线的准线方程是怎样的？方程是怎样的？xyoF相应于上焦点相应于

13、上焦点F(c, 0)的是的是上准线上准线2yac 2yac 相应于下焦点相应于下焦点F(-c, 0)的是的是下准线下准线2yac 2yac F解：解： dMl设设 是是点点到到直直线线 的的距距离离，根根据据题题意意，所所求求轨轨迹迹就就是是集集合合54|MF|PM,d22551645(x)y.|x| 由由此此得得将将上上式式两两边边平平方方，并并化化简简，得得22916144xy.86所所以以点点的的轨轨迹迹是是实实轴轴、虚虚轴轴长长分分别别为为 , ,的的双双曲曲线线M.【例例2 2】点点M M（x x，y y）与定点）与定点F F（5 5，0 0）的距离和它到定）的距离和它到定直线直线

14、的距离的比是常数的距离的比是常数 ，求点，求点M M的轨迹的轨迹. .516:xl45221169xy.即即xyl.FOMd.H归纳总结归纳总结1. 双曲线的第二定义双曲线的第二定义 平面内，若平面内，若定点定点F不在定直线不在定直线l上，则到定点上，则到定点F的的距离与到定直线距离与到定直线l的距离比为常数的距离比为常数e(e1)的点的轨迹是的点的轨迹是双曲线双曲线。 定点定点F是是双曲线的焦点双曲线的焦点，定直线叫做，定直线叫做双曲线双曲线的准线的准线，常数，常数e是是双曲线的离心率双曲线的离心率。2. 双曲线的准线方程双曲线的准线方程对于双曲线对于双曲线22221,xyab 准线为准线为

15、2axc 对于双曲线对于双曲线22221yxab 准线为准线为2ayc 注意注意: :把双曲线和椭圆的知识相类比把双曲线和椭圆的知识相类比.练习题练习题:1.求下列双曲线的实轴和虚轴的求下列双曲线的实轴和虚轴的长、顶点和焦点坐标、离心率、长、顶点和焦点坐标、离心率、渐近线方程和准线方程：渐近线方程和准线方程：422 yxxyOlF点点M(x, y)与定点与定点F(c, 0)的距离和它到定直线的距离和它到定直线 的距离比是常数的距离比是常数 (ca0)，求点，求点M的轨迹的轨迹.cx2aacM解：解：设点设点M(x,y)到到l的距离为的距离为d，则，则|MFcda 即即222()xcycaaxc

16、 化简得化简得(c2a2)x2 a2y2=a2 (c2 a2) 设设c2a2 =b2，22221xyab (a0,b0)故点故点M的轨迹为实轴、虚轴长分别为的轨迹为实轴、虚轴长分别为2a、2b的双曲线的双曲线.222()|axcyacx 22224222(2)2axcxcyaa cxc x b2x2a2y2=a2b2即即就可化为就可化为:M62页页B组组3题题xyoax 或或ax ay ay 或或)0 ,( a ), 0(a xaby xbay ace)(222bac 其其中中关于关于坐标坐标轴和轴和原点原点都对都对称称性性质质双曲线双曲线) 0, 0(12222 babyax) 0, 0(1

17、2222 babxay范围范围对称对称 性性 顶点顶点 渐近渐近 线线离心离心 率率图象图象 xyo椭圆与直线的位置关系及判断方法椭圆与直线的位置关系及判断方法判断方法判断方法0（1）联立方程组）联立方程组（2）消去一个未知数）消去一个未知数（3）复习:相离相切相交二、二、直线与双曲线的位置关系直线与双曲线的位置关系1) 位置关系种类位置关系种类XYO种类种类:相离相离;相切相切;相交相交(0个交点，一个交点，个交点，一个交点，一个交点或一个交点或两个交点两个交点)2)2)位置关系与交点个数位置关系与交点个数XYOXYO相离相离:0:0个交点个交点相交相交:一个交点一个交点相交相交:两个交点两

18、个交点相切相切:一个交点一个交点判断下列直线与双曲线之间的位置关系：判断下列直线与双曲线之间的位置关系：122:3 , :1916xyl yc相相 交交222:2 , :1916xyl xc相相 离离一般情况的研究2222:0) , :1bxyl yx m mcaab（显然显然,这条直线与双曲线的渐进线是平行的这条直线与双曲线的渐进线是平行的,也就是相交也就是相交.把直线方程代入双曲线方程把直线方程代入双曲线方程,看看看判别式如何看判别式如何?根本就没有判别式根本就没有判别式 !但它跟双曲线有一个交点但它跟双曲线有一个交点若若m=0m=0会是怎么的一种情况会是怎么的一种情况判断直线与双曲线位置

19、关系的操作程序判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程把直线方程代入双曲线方程得到一元一次方程得到一元一次方程得到一元二次方程得到一元二次方程直线与双曲线的直线与双曲线的渐进线平行渐进线平行相交（一个交点）相交（一个交点） 计计 算算 判判 别别 式式0=00 直线与双曲线相交（两个交点）直线与双曲线相交（两个交点） =0 直线与双曲线相切直线与双曲线相切 0 直线与双曲线相离直线与双曲线相离利用弦长公式：利用弦长公式：2121xxkAB2122124)(1xxxxk或2122124)(11yyyykAB解：解：由双曲线的方程得，两焦点由双曲线的方程得，两焦点分别为分别为F

20、F1 1(-3,0),F(-3,0),F2 2(3,0).(3,0).F1F2xyOAB222313630 xy F ,A,BAB .【例例 】如如图图，过过双双曲曲线线的的右右焦焦点点倾倾斜斜角角为为的的直直线线交交双双曲曲线线于于两两点点，求求 因为直线因为直线ABAB的倾斜角是的倾斜角是3030，且直线经过右焦点且直线经过右焦点F F2 2，所以，直，所以，直线线ABAB的方程为的方程为333y(x) (1)22333136y(x), xy, 由由256270yxx.消消去去 ，得得12935x,x. 解解这这个个方方程程，得得12122 312 35x ,x y,y. 将将的的值值代代入入（），得得92 332 355A,B(,),( ,).于于是是，两两点点的的坐坐标标分分别别为为221212AB(xx )(yy )所所以以，2292 332 3551635()(). 【提升总结提升总结】这里我们也可以利用弦长公式求解这里我们也可以利用弦长公式求解.弦长公式：弦长公式：2121xxkAB2122124)(1xxxxk或或2122124)(11yyyykAB算一算，算一算，看结果一看结果一样吗？样吗？1 1你你能能求求出出A AF F B B的的周周长