小型蔬菜播种机设计【含19张CAD图纸+说明书+PROE三维模型】
收藏
资源目录

压缩包内文档预览:(预览前20页/共24页)
编号:98652960
类型:共享资源
大小:14.26MB
格式:ZIP
上传时间:2020-10-16
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
含19张CAD图纸+说明书+PROE三维模型
小型
蔬菜
播种机
设计
19
CAD
图纸
说明书
PROE
三维
模型
- 资源描述:
-


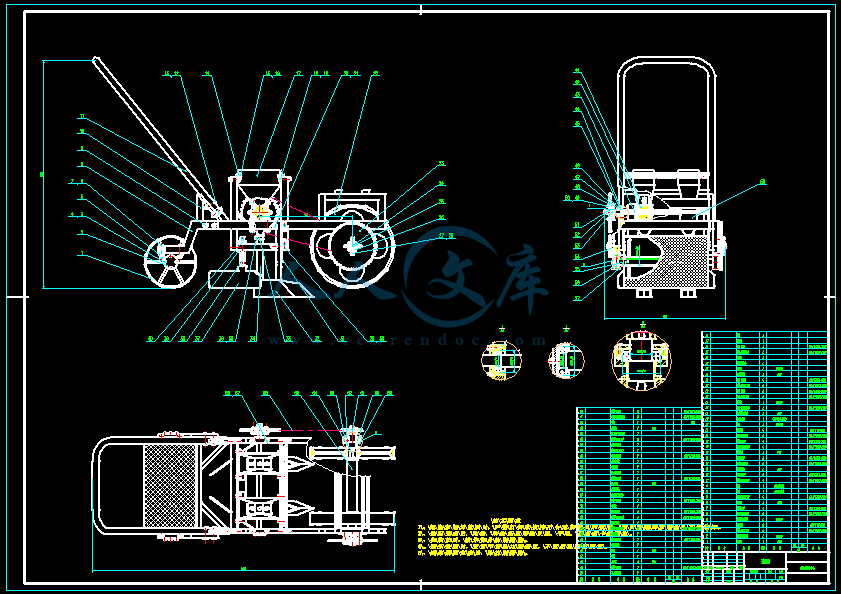
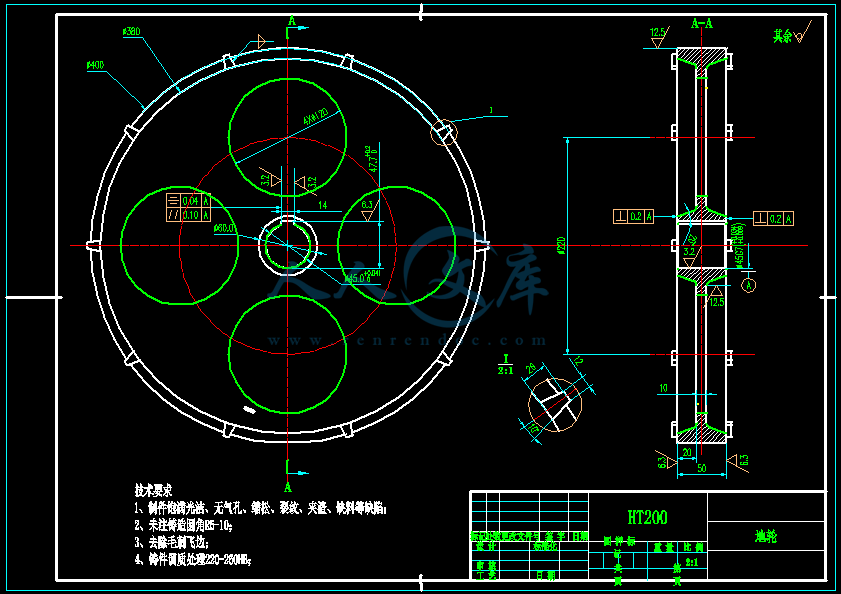
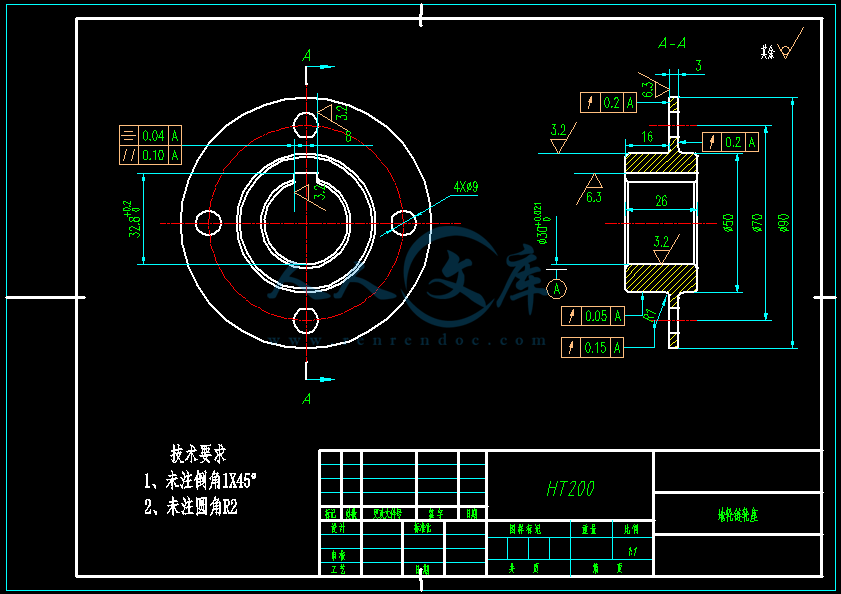



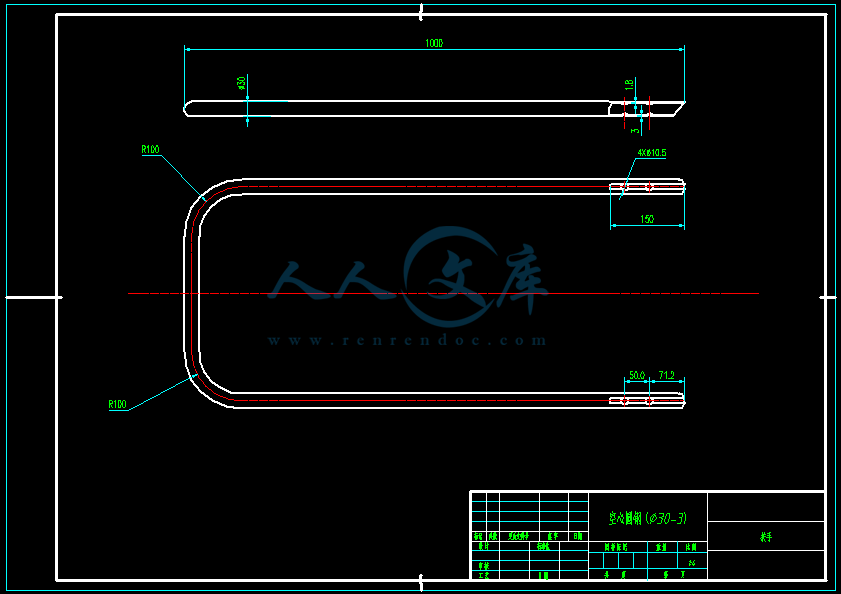

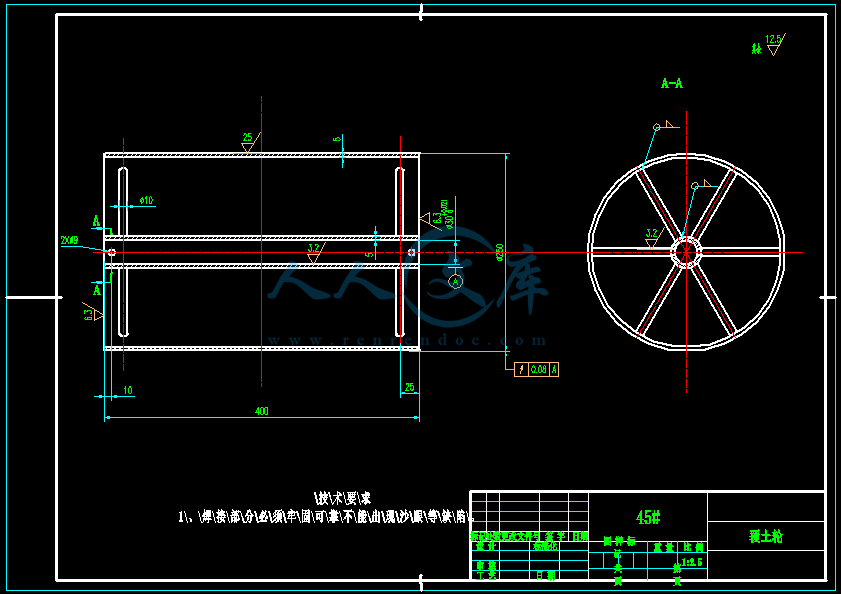
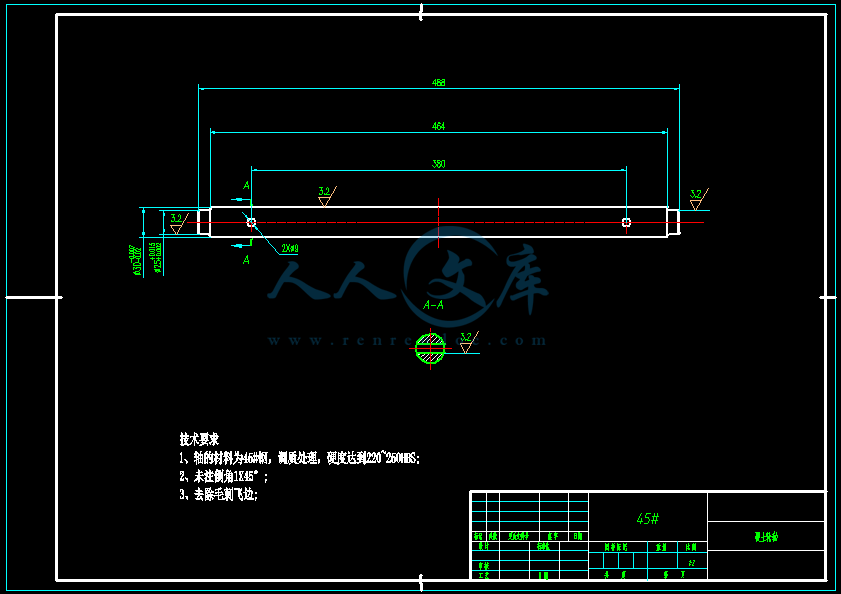
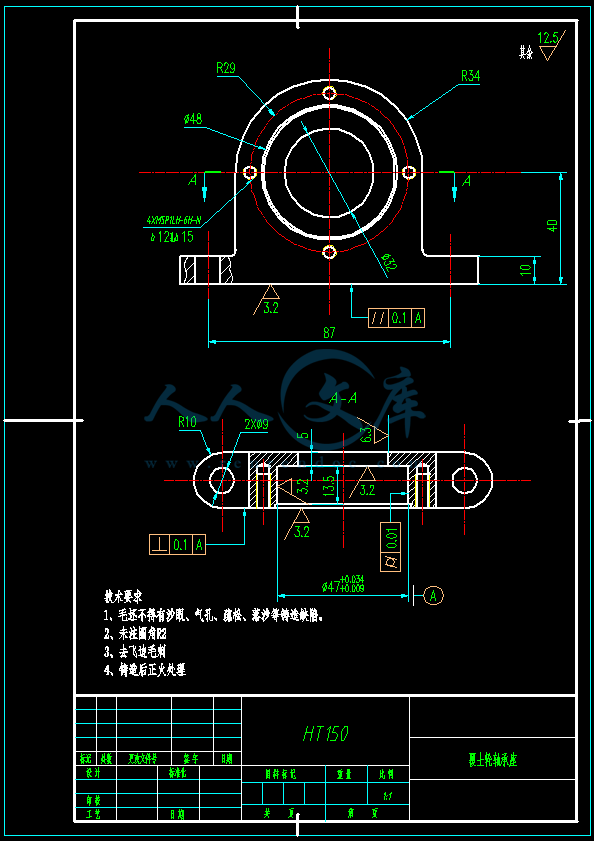

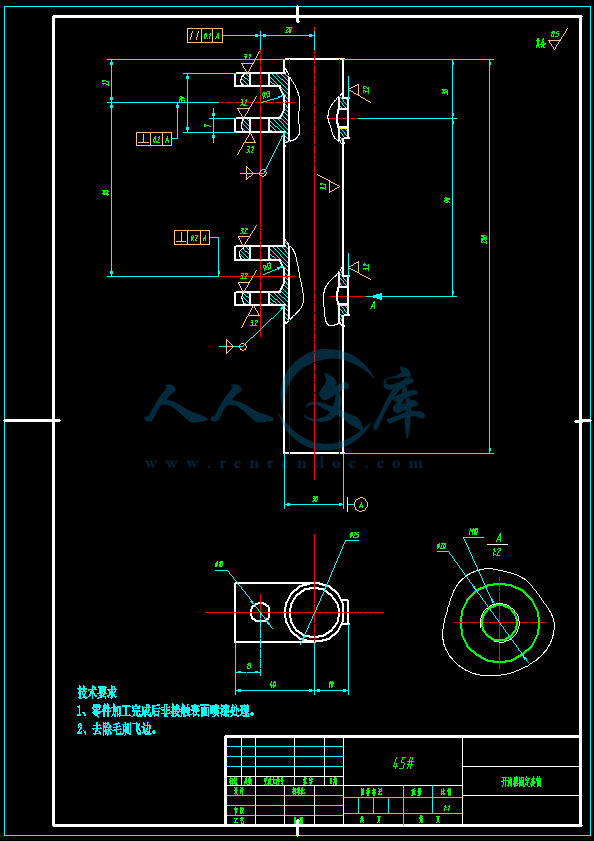
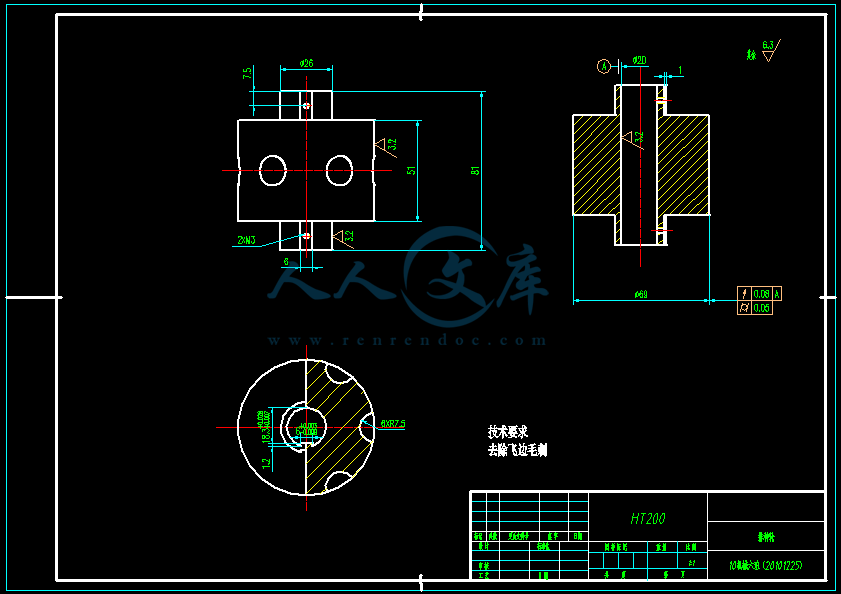


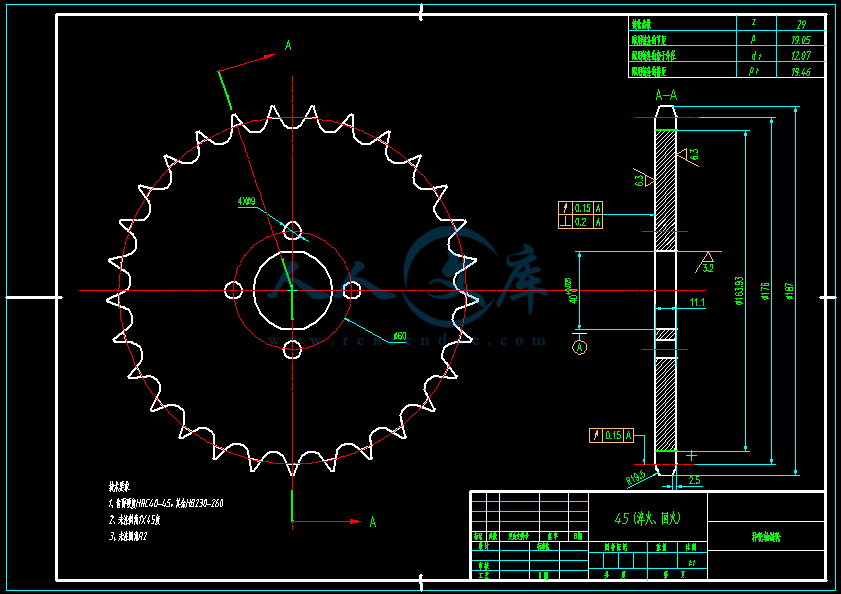
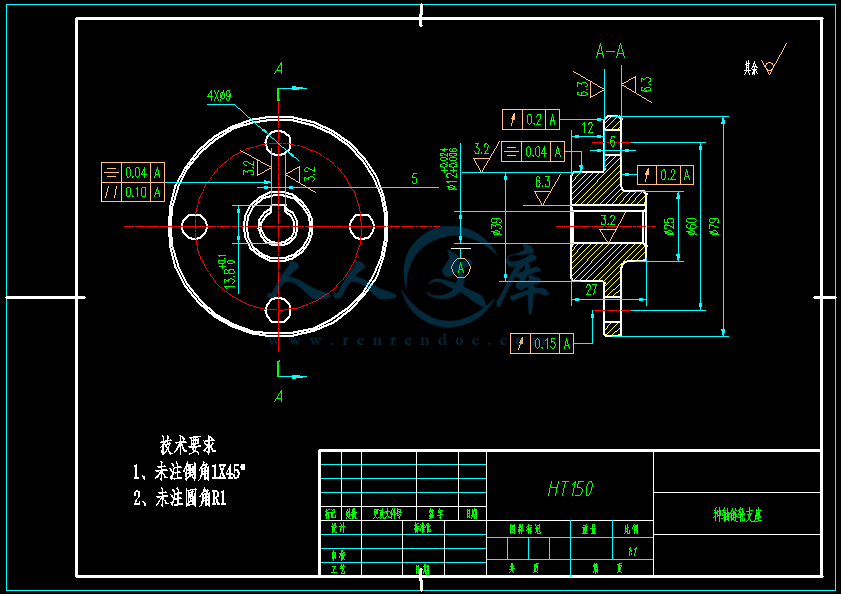
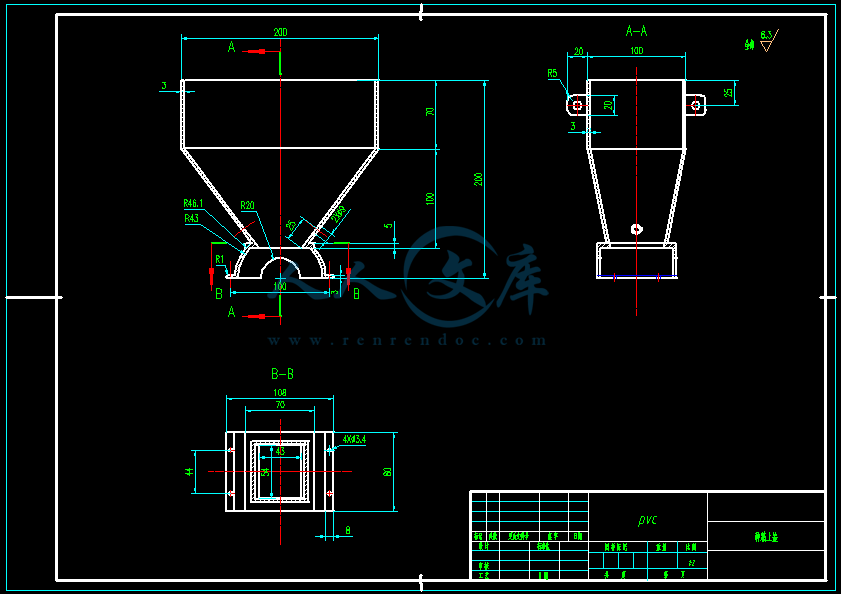
- 内容简介:
-
毕业设计(论文)翻译 学生姓名: 学院: 机电工程学院 专 业: 机械设计制造及自动化 设计(论文)题目: 小型蔬菜播种机的设计 指导教师: 年4月10日Mathematical Modelling of Vacuum Pressure on a Precision SeederAbstractThe purpose of this research was to determine the optimum vacuum pressure of a precision vacuum seeder and to develop mathematical models by using some physical properties of seeds such as one thousand kernel mass, projected area, sphericity and kernel density. Maize, cotton, soya bean, watermelon, melon, cucumber, sugarbeet and onion seeds were used in laboratory tests. One thousand kernel mass, projected area, sphericity and kernel density of seeds varied from 4.3 to 372.5g, 577mm2, 38.485.8% and 4401310kgm3, respectively. The optimum vacuum pressure was determined as 4.0kPa for maize I and II; 3.0kPa for cotton, soya bean and watermelon I; 2.5kPa for watermelon II, melon and cucumber; 2.0kPa for sugarbeet; and 1.5kPa for onion seeds. The vacuum pressure was predicted by mathematical models. According to the results, the final model could satisfactorily describe the vacuum pressure of the precision vacuum seeder with a chi-square of 2.51103, root mean square error of 2.74102 and modelling efficiency of 0.99. Nomenclature Nomenclature a, b, c, d, e regression coefficients Em modelling efficiency Erms root mean square error kexp experimental vacuum pressure, kPa kexp, mean mean value of experimental vacuum pressure, kPa kpre predicted vacuum pressure, kPa L length, mm m1000 one thousand kernel mass, g N number of observation n number of constants in the model P projected area, mm2 Pv vacuum pressure, kPa p probability R2 coefficient of determination T thickness, mm W width, mm sphericity, % 2 chi-square k kernel density, kgm3Article OutlineNomenclature 1. Introduction 2. Literature review 3. Materials and methods 4. Results and discussion 5. Conclusions Acknowledgements References1. IntroductionPrecision sowing has been a major thrust of agricultural engineering research for many years; however, most of the research and development work has dealt with seeders for agronomic crops. The main purpose of sowing is to place the seed to a certain space and a depth in the seedbed. Precision seeders place seeds at the required spacing and provide a better growing area per seed. There are two common types of precision seeders: belt and vacuum. Precision vacuum seeders have a metering plate with metering holes on a predetermined radius. A vacuum is applied to these metering holes by means of a race machined in a backing plate. As the plate rotates, the vacuum applied to the metering holes enables them to pick up seeds from the seed hopper. Precision vacuum seeders have the following advantages over the mechanical seeders: better working quality, more precise seed rates with lower rate of seed damage, better control and adjustment of upkeep and drift of seeds, and broader spectrum of applicability (Soos et al., 1989). A seeder should place a seed in an environment in which the seed will reliably germinate and emerge. A number of factors affect the spacing of plants. The seed selection mechanism may fail to select or drop a seed resulting in large spacing between seeds. The mechanism may select and drop multiple seeds resulting in small spacings between seeds. Seed quality, soil conditions, seeder design and the skill of the operator all play a part in determining the final plant stand. The physical properties of seeds are essential for the design of equipment for handling, processing, storing and sowing the kernels. Various types of cleaning, grading, separation and sowing equipment are designed on the basis of the physical properties of seeds. However, no model has been found to describe seeder parameters such as vacuum pressure related with physical properties of seeds. The physical properties of the seeds are the most important factors in determining the optimum vacuum pressure of the precision vacuum seeder. In this study, using some of these, e.g. one thousand kernel mass, projected area, sphericity and kernel density, mathematical models were developed to predict optimum vacuum pressure. The experimental values of vacuum pressure were determined from laboratory test procedure. 2. Materials and methodsThe laboratory test procedure involved testing the metering uniformity of the seeder at the different vacuum pressure with the different seeds: two different maize varieties (maize I and maize II), cotton, soya bean, two different watermelon varieties (watermelon I and watermelon II), melon, cucumber, sugarbeet and onion. These seeds represent several seed shapes varying from spherical (soya bean, maize II) to flat and elongated (maize I, melon, watermelon, cucumber). Two different varieties of maize and watermelon seeds were selected, because of the more diverse range of one thousand kernel mass, projected area, sphericity or kernel density than other seeds. All seeds used in this research were uncoated seed. The main dimensions of the seeds are given in Table 1. The seeder was set to space the seeds as closely to the recommended spacing as possible. Table 1. Means and standard errors of the seed dimensions A grease belt test stand was used to determine sowing uniformity of each seed at the different vacuum pressures. This particular test stand had a 150mm wide belt with a 75m long horizontal viewing surface. A seeder row unit was mounted on a greased belt test stand which utilised an adjustable speed drive mechanism to operate the seed metering devices at a known constant speed. Sufficient oil was added to the top surface of belt to capture the seed as it was released from seeder unit without rolling or bouncing of seed on the belt surface. A wide variety of measures were used to qualify seeder performance with regard to plant spacing (Brooks & Church, 1987; Karayel & zmerzi, 2001; Jasa & Dickey, 1982). Some tests used performance measures involving distance between plants in the field. Other tests used performance measures involving distance between seeds on grease belt test stand or by opto-electronic sensor system ( Bracy et al., 1998; Smith et al., 1991; Lan et al., 1999). A few tests used performance measures involving distance between seeds sown into soil ( Panning, 1997). A precision vacuum seeder unit was operated in all treatments (Fig. 1). The seeder unit was a general purpose seeder designed for row crops such as maize and soya beans. Three different vacuum plates with different hole diameters were used in the metering mechanism. The diameter of vacuum plates were 230mm. The holes were drilled along a 200mm diameter pitch circle. The holes of the vacuum plate were 35mm in diameter for maize I, II, soya bean and cotton; 25mm in diameter for watermelon I, II, melon, and cucumber and 15mm in diameter for sugarbeet and onion. The seed plate operated in a vertical plane. Air suction from the holes of the seed plate caused the seed to stick to the holes. The stuck seed was released from the rotating plate by temporarily preventing airflow. The absence of suction allowed the seed to be dropped into soil. It had no seed tube and the seed fall height (12mm) of the seeder was kept low in order to reduce the chance of non-uniform spacing which can occur due to the bouncing of seed, if dropped from high plane. The vacuum level was regulated by adjusting the size of an opening in the vacuum line of seeder and measured with a manometer. Fig. 1. The metering mechanism of the precision vacuum seeder: 1, vacuum plate; 2, seed; 3, seed box; 4, air suction canal; 5, air cut; 6, furrow opener The seeder was operated over the greased belt at a ground speed of 1ms1 and adjusted to four vacuum pressures 2.0, 3.0, 4.0 and 5.0kPa for maize I, II, soya bean and cotton; 2.0, 2.5, 3.0 and 3.5kPa for melon, watermelon I, II and cucumber; 1.0, 1.5, 2.0 and 2.5kPa for sugarbeet and onion seeds. Seed spacings were measured over a distance of 7m. The seeder was adjusted to deliver a nominal seed spacing of 230mm for maize I and II, 170mm for cotton, 105mm for soya bean, 550mm for watermelon I, II, melon and cucumber, 150mm for sugarbeet and 85mm for onion. The sowing uniformity was analysed using the methods as described by Kachman and Smith (1995). The multiple index is the percentage of spacings that are less than or equal to half of the theoretical spacing and indicates the percentage of multiple seed drops. The miss index is the percentage of spacings greater than 1.5 times the theoretical spacing and indicates the percentage of missed seed locations or skips. Quality of feed index is the percentage of spacings that are more than half but no more than 1.5 times the theoretical spacing. Quality of feed index is 100% minus miss and multiple index and indicates the percentages of single seed drops. Preciseness is the coefficient of variation of the spacings that are classified as singles after omitting the outliers consisting of misses and multiples. Kachman and Smith (1995) recommended using miss index, multiple index, quality of feed index and preciseness for summarising the uniformity of seeder metering rather than mean or sample coefficient of variation. They concluded that several measures were needed to give a true picture of seeder uniformity. For this study, miss index, multiple index, quality of feed index and preciseness are reported. Various physical properties of seeds including kernel density, projected area, sphericity and one thousand kernel mass are the most important factors in determining the optimum vacuum pressure of the precision vacuum seeder (Barut, 1996). The physical properties of the seeds were determined by the following methods: Linear dimensions, i.e. length, thickness and width were measured by using a vernier caliper with a sensitivity of 0.01mm. Sphericity were calculated by using the following equation (Mohsenin, 1970):(1)where: L is the length; W is the width; and T is the thickness in mm. One thousand kernel mass was measured by an electronic balance with a sensitivity of 0.001g. Kernel density was measured by the liquid displacement method. Toluene (C7H8) was used rather than water because it was not absorbed by fruits (Mohsenin, 1970; gt, 1998). Projected area was determined by using a digital camera (Kodak DC 5000) and Sigma Scan Pro 5 program. For the estimation of the vacuum pressure, in relation to kernel density, projected area, sphericity and one thousand kernel mass, mathematical models were developed. The suitability of the final model was compared and evaluated using chi-square, root mean square error and modelling efficiency. Chi-square 2, root mean square error Erms and modelling efficiency Em were calculated as follows:(2)(3)(4)where: kexp is the experimental vacuum pressure in kPa; kexp,mean is the mean value of experimental vacuum pressure in kPa; kpre is the predicted vacuum pressure in kPa; N is the number of observations; and n is the number of constants in the model. Reduced chi-square is the mean square of the deviations between the experimental and calculated values for the models and, is used to determine the goodness of the fit. The lower values of the reduced chi-square, the better the goodness of the fit. The root mean square error shows the deviations between the calculated and experimental values and it requires to reach zero. The modelling efficiency also shows the ability of the model and its highest value is 1 (Yaldiz et al., 2001; Ertekin & Yaldiz, 2004). Each experiment was arranged as a randomised complete block (Neter et al., 1990) and replicated five times. An analysis of variance method was applied to analyse data sets using a statistical software package SAS. Duncans multiple-range tests were used to identify significantly different means within dependent variables. 3. Results and discussionThe effect of vacuum pressure on sowing uniformity of the vacuum seeder was analysed relating to the multiple index, miss index, quality of feed index and preciseness. Multiple index, miss index and quality of feed index were combined for analysis of variance to determine the significant difference in the variability among the parameters. The results of this analysis are given in Table 2, Table 3 and Table 4. All measurement of sowing uniformity of the vacuum seeder were affected by vacuum pressure. Table 2. The sowing uniformity of the vacuum seeder with maize I and II, cotton and soya bean seeds for different vacuum pressure Note: Means within a group followed by same letter are not significantly different at probability p=005, by Duncans multiple range test.Table 3. The sowing uniformity of the vacuum seeder with watermelon I and II, melon and cucumber seeds for different vacuum pressure Note: Means within a group followed by same letter are not significantly different at probability p=005, by Duncans multiple range test.Table 4. The sowing uniformity of the vacuum seeder with sugarbeet and onion seeds for different vacuum pressure Note: Means within a group followed by same letter are not significantly different at probability p=0.05, by Duncans multiple range test.The optimum vacuum pressure was determined for each seed according to quality of feed index and preciseness. As can be seen from laboratory study results in Table 2, Table 3 and Table 4, the highest seed spacing uniformities (quality of feed index) and the lowest preciseness values were obtained at the vacuum pressure of 4.0kPa for maize I and II; 3.0kPa for cotton, soya bean and watermelon I; 2.5kPa for watermelon II, melon and cucumber; 2.0kPa for sugarbeet and 1.5kPa for onion seeds. The most uniform sowing uniformity was obtained with soya bean seeds at any vacuum pressures. Uniform, spherical seeds such as soya bean and maize II were easy to meter with the vacuum metering system. The miss index decreased and the multiple index increased with increasing vacuum pressure for all seeds. Multiple seed drops were more common than misses for watermelon I and II, melon, cucumber, onion and sugarbeet seeds. Few skips or multiple drops occur at any vacuum pressure for maize I and II, cotton and soya bean seeds. Loss of uniformity of the vacuum seeder was probably a combination of several factors. The results support reports from Barut (1996) who found that the pattern efficiency of the vacuum plate differed most at lower or higher vacuum pressures and faster wheel speeds. In this research, preciseness and quality of feed index of the vacuum seeder were poorer at the lower and higher vacuum pressures than optimum vacuum pressure. One thousand kernel mass, projected area, sphericity and kernel density of seeds are given in Table 5. One thousand kernel mass, projected area, sphericity and kernel density of seeds varied from 4.3 to 372.5g, 577mm2, 38.485.8% and 4401310kgm3, respectively. Table 5. Means and standard errors of the seed dimensions The relationship between one thousand kernel mass, projected area, sphericity and kernel density with vacuum pressure presented in Fig. 2, Fig. 3, Fig. 4 and Fig. 5. For the determination of the relationship between the one thousand kernel mass and the projected area with vacuum pressure, the power model was used. For the determination of relationship between the sphericity and the kernel density with the vacuum pressure, the linear model was used. The diagrammatic representation of the models results in a curve that fits well for the description of the vacuum pressure. The relationship between one thousand kernel mass with vacuum pressure is better than the others with the highest coefficient of determination of 0.92. Fig. 2. Vacuum pressure of precision vacuum seeder as a function of one thousand kernel mass; R2, coefficient of determination Fig. 3. Vacuum pressure of vacuum seeder as a function of projected area; R2, coefficient of determination Fig. 4. Vacuum pressure of vacuum seeder as a function of sphericity; R2, coefficient of determination Fig. 5. Vacuum pressure of vacuum seeder as a function of kernel density; R2, coefficient of determination All possible combinations of the different variables were tested and included in the regression analysis. The multiple combinations of one thousand kernel mass, projected area, sphericity and kernel density that gave the lowest root mean square error and chi-square and the highest modelling efficiency were finally included in the final model. Based on the multiple regression analysis the accepted model constants, coefficients, chi-square 2, root mean square error Erms and modelling efficiency Em were as follows:Pv=a+bm1000027+cP002d+ekwhere: Pv is the vacuum pressure in kPa; m1000 is one thousand kernel mass in g; P is the projected area in mm2; is the sphericity in %; k is the kernel density in kgm3. The optimum values of the coefficient a, b, c, d, and e, namely 1.00, 0.72, 2.09103, 0.01 and 0.37103, respectively, gave values for 2 of 2.51103, for Erms of 2.74102, and for Em of 0.99. Validation of the established final model was evaluated by comparing the computed vacuum pressures with the observed vacuum pressures. The performance of the model was illustrated in Fig. 6. The predicted data generally banded around the straight line which showed the suitability of the final model in describing vacuum pressure of the seeder. Fig. 6. Experimental versus predicted vacuum pressure values by final model; R2, coefficient of determination 4. ConclusionsIn laboratory tests, the optimum vacuum pressure of a precision vacuum seeder was determined as 4.0kPa for maize I and II; 3.0kPa for cotton, soya bean and watermelon I; 2.5kPa for watermelon II, melon and cucumber; 2.0kPa for sugarbeet and 1.5kPa for onion seeds. In order to predict vacuum pressure in relation to one thousand kernel mass, projected area, sphericity and kernel density of seeds, mathematical models were developed. The relationship between one thousand kernel mass with vacuum pressure was better than the others with the highest coefficient of determination. The final model could satisfactorily describe the vacuum pressure of the precision vacuum seeder with a chi-square of 2.51103, root mean square error of 2.74102 and modelling efficiency of 0.99. Acknowledgements The corresponding author acknowledge the help of Dr. Can ERTEKIN in developing the mathematical models. 真空压力播种机的数学建模引言 这项研究的目的是确定最佳的精密真空压力播种机。通过运用种子的一些物理性质如每1000粒种子的质量,表面积、圆度和种子密度来建立数学模型.。分别取玉米、棉花、大豆、西瓜、甜瓜、黄瓜、甜菜、洋葱的种子作为实验对象。结果,每1000粒种子质量、表面积、圆度和种子密度分别为4.3-372.5g、 5-77m2、38.485.8%、440-1310千克/m3。最佳的真空压力:玉米种子(I、II)为4kPa;棉花、黄豆和西瓜(I)种子为3kPa;西瓜(II)、甜瓜和黄瓜种子为2.5kPa;甜菜种子为2kPa;洋葱种子为1.5kPa。最终,数学模型能准确模拟出真空压力。研究结果显示:模型能准确地模拟出精密真空压力播种机的真空度为2.5110-3; 均方根误差为2.7410-2。模拟效率率高达99%。各参数含义回归系数: a,b,c,d,e模型效率:Em均方根误差:Erme试验真空压力 (kPa):Kexp试验真空压力平均值(kPa): Kexp.mean真空预压(kPa):Kpre长度(mm):L每千粒种子质量(g):m1000种子数目:N模型种子数常量:n表面积(mm2):P真空压力(kPa):Pv概率:p确定系数:R2厚度(mm):T宽度(mm):W圆度(%):方差:x2种子密度(kg/m3):k文章概要标题1.引言2.材料和方法3.结果与讨论4.结论5.致谢6.参考资料1.引言精密播种作为主要农业工程研究已经多年。所以,大部分的研究和开发成果已经运用到了农业播种。现在,研究的主要目的是把种子播到一定深度的苗床上。精密播种机必须让种子之间有一定间隔,以适应种子生长。现在,有两种类型的精密播种机:皮带播种机和真空压力播种机。真空压力播种机有一带有固定半径计量孔的真空计量板。计量板应用这些计量手段洞竞赛通过一回收装置. 由于平板旋转、真空所产生的压力使种子从这些孔中漏出. 精密真空压力播种机具有以下优点:更好的工作质量、较低种子损害率、更好地控制和保护种子、还有广泛的适用性。 精密播种机需要把种子播种在一个可靠的环境,使种子发芽并生长。很多因素包括种子间距都能影响种子生长,种子选择装置可能未选中种子或使种子间间隔过大或过小。还有,种子质量、土壤条件、播种机的设计与工人的操作技巧都是影响种子播种位置正确与否的因素。 种子的物理特性对处理,加工,储藏和播种装备的设计极为重要。各种清洗、分级、分类及播种设备都是基于种子的物理特性设计的。不过,一直没有找到模型来描述真空压力播种机的参数及物理性能。种子的物理特性在选择最适合的精密真空压力播种机时是最重要的因素。在这项研究中,用一些例子,例如,每1000粒种子的质量,表面积、圆度和种子密度建立的数学模型来预测最佳真空压力。真空压力试验的测定值是从实验室测试程序中得出的。2.材料和方法实验室运用统一的标准测试在不同的真空压力下的不同种子:两种不同的玉米品种(玉米I、玉米II)、棉花、黄豆、 两种不同的西瓜品种(西瓜I和西瓜II),甜瓜、黄瓜、甜菜、洋葱。 这些种子是由几个不同形状球形种子(黄豆、玉米II)单位、芒(玉米I、 甜瓜、西瓜、黄瓜)。选择两种不同品种玉米和西瓜种子,是因为两个不同品种的种子比其他种子的质量,表面积、圆度和种子密度更有多样性。所有在这研究使用的种子都是剥掉外壳的,其主要尺寸在表1中列出。 这些种子都是在紧密排列下被测量的。表1. 种子尺寸和标准误差种子长度(mm)厚度(mm)宽度(mm)玉米 I11.960.224.740.068.870.13玉米 II9.960.196.82.0098.250.11棉花9.980.205.200.079.520.12黄豆8.010.135.890.076.900.08西瓜 I8.30.142.100.036.500.09西瓜 II7.410.142.250.035.850.09甜瓜11.40.1920350.0440620.08黄瓜10.520.191.600.023.930.07甜菜40760.0720450.0430840.07洋葱2.170.031.230.021.400.04皮带试验台是一种在不同的真空压力下用油脂来保证每个种子播种均匀的装置。 这个试验装置用150毫米宽、7.5米长的皮带来观察其表面种子播种的均匀程度。播种机被排列固定在试验台上,表面被涂上油脂的皮带在调速装置作用下以恒定的速度前进。由于油脂的作用使种子被固定在皮带表面,这样,就保证了种子间的距离 (Brooks & Church, 1987; Karayel & zmerzi, 2001; Jasa & Dickey, 1982)。有些试验是关于在野外植株之间的距离。而另一些试验是关于种子在油脂皮带上的距离或者通过光电感应系统( Bracy et al., 1998; Smith et al., 1991; Lan et al., 1999)。还有些实验是涉及在土壤播种是种子之间的距离( Panning, 1997)。一个精密真空压力播种机单位是被在所有的处理中运作中的(图1)。播种机是专为连续播种农作物如玉米、大豆等的播种而发明的。三种不同真空板孔直径分别用不同的计量机制。直径230毫米的真空板。洞是沿着一直径200毫米的圆钻钻的。3.5毫米直径孔的真空板是为玉米(I、II)、大豆和棉花设计的。2.5毫米直径孔的真空板是为西瓜(I、II)、甜瓜、黄瓜和直径为1.5毫米甜菜、洋葱设计的。真空板是垂直地面的,空气的压力使种子嵌在板的孔中。被释放出来的种子由于气流的作用暂时在旋转盘中。最后掉落到了土壤中。如果种子没有管子(直径12mm)的引导直接从高空下落,则会散落不均和弹起。真空的大小是通过调整播种机真空线上开口的大小和压力计测量控制的。精确真空压力播种机的机械装置:1.真空板;2.种子;3.种子盒;4.空气吸水道;5.空气切口;6.开沟器在皮带带动下播种机的速度为1m/s,当播种玉米(I、II)、黄豆和棉花种子时压力为2.0、3.0、4.0和5.0 kPa;甜瓜、西瓜(I、II)、黄瓜时压力为2.0、2.5、3.0和3.5 kPa;甜菜、洋葱时压力为1.0、1.5、2.0和2.5 kPa。种子间距可超过7米。播种机可调整种子间距玉米(I、II)为230mm,棉花为170mm,黄豆为105mm,西瓜(I、II)、黄瓜、甜瓜为550mm,甜菜为150mm,洋葱为85mm。Kachman 和Smith 早在1995已经提出播种均匀分析方法。倍数指数显示种子间距小于或等于理论上调节间隔的一半。误差指数显示间距大于理论间隔的1.5倍,还显示有种子不能准确下落。种子播种质量综合指数显示间距百分比都超过了半数,但都超不过1.5倍。精确的变化参数在省略去包括误差和倍数等因素以后被单独分类。Kachman and Smith (1995)介绍了误差指数、倍数指数、质量综合指数和播种机均匀样品而非抽样检查变化的协同因素。他们的结论是,有必要采取一些措施,让实播种机播种更均匀。这项研究的误差指数、倍数指数、质量综合指数和播种精确度都被报道了。各种物理性能包括种子核密度、表面积、圆度、每1000粒种子质量是选择精密真空压力播种机的最重要因素。种子的物理性能测定方法如下:线性尺寸,即长、宽、厚分别用游标卡尺测量用0.01毫米的灵敏度。圆度利用下列公式计算(Mohsenin, 1970):(1)注:L是长度; W是宽度; T是厚度(mm)每1000种子质量采用灵敏度为0.001g的电子秤。种子核密度测量用液体位移法. 用甲苯(c7h8)而非水是因为它不能被种子吸收(Mohsenin, 1970; gt, 1998)。表面积用数码相机(柯达直流5000)、射线扫描得出。关于种子核密度、表面积、圆度、每1000粒种子质量模拟的数学模型已经作出。适合最终使用和评估的模型是比较方差、均方根误差和模拟效率。方差(2)、均方根误差(Erme)和模型效率(Em)如下:(2)(3)(4) 注: Kexp表示实验的真空压力,单位kPa; Kexp.mean是实验真空压力平均值(kPa); Kpre是真空预压(kPa); n为观测次数; N是常数。减小平方差的偏差值来改变模型确定最适合的数据。减小的值越低越适合。它要求均方根误差和实验之间的偏差值达到零。模型效率则显示模型的可行性,它的最高值是1。(Yaldiz et al., 2001; Ertekin & Yaldiz, 2004)每个实验都随机地做五遍,使用SAS软件分析方差和统计分析数据。用Duncan的多范围测试方法来鉴别差异。3、结果与讨论分析得出播种机真空压力对播种效果影响与误差指数、倍数指数、质量综合指数和播种精确度相关。对误差指数、倍数指数、质量综合指数和播种精确度平方差的综合分析,以确定参数之间的区别。结果分析在表1、表2和表3中。表2. 真空播种机在不同的压力下对玉米(I)、(II),棉花和大豆种子播种的均匀性分析。真空压力(kPa)播种精确度%倍数指数%误差指数%质量指数%玉米 I2.015.30.4c10.7a88.9b3.011.03.6b6.8b89.6b4.010.83.2b2.2c94.5a5.014.18.8a1.3c89.9b玉米 II2.013.40.2c9.8a90.0c3.011.71.4b8.4a90.2b4.08.90.3c3.9b95.9a5.011.94.5a3.2b92.3b棉花2.014.82.3b9.4a88.3b3.012.12.6b5.2c92.2a4.014.213.0a7.6b91.0a5.015.313.5a2.9d83.6c黄豆2.07.50.0b8.2a91.8b3.06.50.0b4.3b95.6a4.06.82.9a3.9c93.1b5.07.73.2a4.0c9
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号