2024-2025学年新疆乌鲁木齐四十一中高二（上）期末数学试卷（含答案）VIP

第=page11页，共=sectionpages11页2024-2025学年新疆乌鲁木齐四十一中高二（上）期末数学试卷一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。1.已知空间三点A(3,2,0)，B(6,1,−2)，C(5,−1,1)，则以AB，AC为邻边的平行四边形的面积为(

)A.72 B.7 C.732.已知正方体ABCD−A1B1C1D1中，O1，O分别为上底面A1A.BO1 B.AA1 C.3.已知A(2,1,3)，B(1,3,4)，C(4,−1,3)，则AB在AC方向上的投影向量的坐标为(

)A.(2,−2,0) B.(32,−32,0)4.已知直线l：ax−2by+c+ab=0(a,b,c>0)与圆O：x2+yA.1 B.12 C.13 5.由直线y=x+1上的点向圆(x−3)2+(y+2)2A.17 B.32 C.6.已知圆M：(x−1)2+(y−2)2=2与圆N：A.15 B.17 C.21 D.237.已知焦点在y轴上的椭圆C：x24+y2mA.32 B.55 C.8.已知抛物线C：y2=4x的焦点为F，P为C上一点，A(2,1)，当△PAF的周长最小时，△PAF的面积为(

)A.78 B.1 C.74 二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。9.如图，在棱长为1的正四面体P−ABC中，O为底面ABC的重心，G，F分别为线段PO，PC上的点(不含端点)，D，E分别为PA，PB延长线上的点，PD=xPA，PE=yPB，PF=zPC，DF交AC于M，EF交BC于NA.若x=y，则MN//平面PAB

B.PO=12PA+13PB+16PC

C.若z=12且平面DEF过点O，则x+y的最小值为4

D.若G10.若一个以(2,−4)为圆心，4为半径的圆，则下列结论正确的是(

)A.直线x=0与圆相切

B.圆关于直线y=−2x对称

C.对∀a∈R，直线ax−y−2a−1=0与圆都相交

D.P(x,y)为圆上任意一点，则(x+1)11.已知点P(0,−2)，Q(0,2)，动点M(x,y)与P，Q两点连线的斜率分别为k1，k2且k1k2=λ(λA.若λ<0，则动点M(x,y)一定在椭圆上

B.若λ>0，则动点M(x,y)一定在双曲线上，且双曲线的焦点在y轴

C.若λ=−4，则x+y的取值范围是[−5,5]

D.若λ=−1，O为坐标原点，且直线x+y+t=0三、填空题：本题共3小题，每小题5分，共15分。12.若a=(1,λ,2)，b=(2,−1,2)，c=(1,4,4)，且a，b，c共面，则λ=13.设m∈R，若三个不同的点A(2,0)、B(m,2)、C(2m−2,2−m)都在直线l上，则m的值为______．14.将双曲线C：x2−y2b2=1(b>0)经过平移和旋转后，得到的新双曲线C′是以O(0,0)为一个焦点，且C′过点四、解答题：本题共5小题，共60分。解答应写出文字说明，证明过程或演算步骤。15.(本小题12分)

如图，已知等腰梯形ABCD，AB=4，CD=6，AD=5，E，F分别为AB，CD的中点，沿线段EF将四边形AEFD翻折到四边形EFNM的位置，点P为线段NC上一点，且满足NP=23NC．

(1)证明：BP//平面EFM；

(2)设二面角M−EF−B的平面角为θ(0<θ<π)，在四边形AEFD翻折过程中，是否存在θ，使得MF16.(本小题12分)

在三棱柱ABC−A1B1C1中，已知底面正三角形边长为2，三棱柱的高为3．

(1)建立适当的直角坐标系，标出所有点的坐标；

(2)设AA1中点为点E，BC中点为点F，求出EC17.(本小题12分)

若集合A表示由满足一定条件的全体直线组成的集合，定义：若集合A中的每一条直线都是某圆上一点处的切线，且该圆上每一点处的切线都是A中的一条直线，则称该圆为集合A的包络圆．

(1)若圆E：x2+y2=4是集合A={(x,y)|ax+by=2}的包络圆．

(i)求a，b满足的关系式；

(ii)若3a+4b+t=0，求t的取值范围；

(2)若集合A={(x,y)|xcosθ+(y+6)sinθ+62=0,θ∈R}的包络圆为C，P是C上任意一点，判断y轴上是否存在定点M，N18.(本小题12分)

已知△ABC的周长为定值，O(0,0)、A(−3,0)、B(3,0)，∠C的最大值为2π3．

(1)求动点C的轨迹E的方程；

(2)D为E的左顶点，过点(1,0)且不与坐标轴垂直的直线与E交于M、N两点，线段MN的中点为P，记直线OP的斜率为k，△DMN19.(本小题12分)

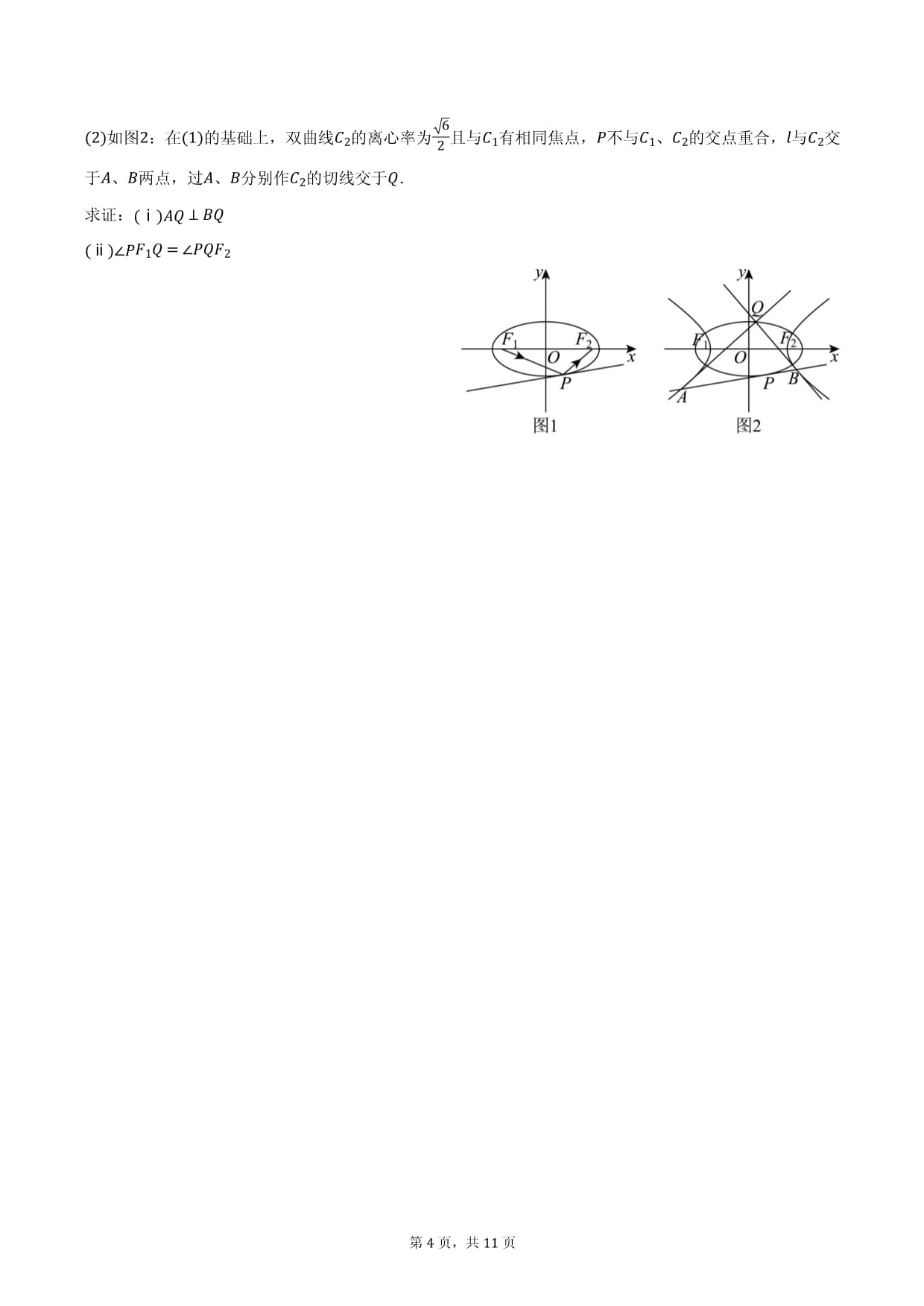
椭圆的光学性质在物理学中有主要应用：如图1，在椭圆C1：x24+y2=1上有一点P(x0,y0)，F1、F2分别为其左、右焦点，过P作直线l与C1切于P，则直线PF1、PF2与l的夹角大小相等．

(1)求证：l的方程为：xx04+yy0=1；

(2)如图2：在(1)的基础上，双曲线C2的离心率为6

参考答案1.C

2.A

3.D

4.C

5.A

6.D

7.B

8.A

9.ACD

10.BCD

11.BCD

12.1

13.−2

14.(3615.(1)证明：取NF的靠近点F的三等分点Q，连接EQ，PQ，

因为NP=23NC，即点P是CN的靠近点C的三等分点，

所以PQ//CF，PQ=23CF=2，

而BE/​/CF，BE=2，

所以PQ//BE，PQ=BE，即四边形PBEQ是平行四边形，

所以BP//EQ，

又BP⊄平面EFM，EQ⊂平面EFM，

所以BP/​/平面EFM．

(2)解：在等腰梯形ABCD中，因为E，F分别为AB，CD的中点，

所以EF⊥CD，EF=AD2−(DF−AE)2=5−(3−2)2=2，

翻折后，EF⊥CF，EF⊥NF，

所以∠NFC就是二面角M−EF−B的平面角，即∠NFC=θ(0<θ<π)，

又CF∩NF=F，CF、NF⊂平面CFN，所以EF⊥平面CFN，

以F为原点建立如图所示的空间直角坐标系，

则F(0,0,0)，C(0,3,0)，B(0,2,2)，E(0,0,2)，

因为NF=3，ME=2，所以N(3sinθ,3cosθ,0)，M (2sinθ,2cosθ,2)，

设P(x,y,0)，

因为CP=13CN，所以(x,y−3,0)=13(3sinθ,3cosθ−3,0)，

解得x=sinθ，y=cosθ+2，即P(sinθ,cosθ+2,0)，

所以FM=(2sinθ,2cosθ,2)，EB=(0,2,0)，EP=(sinθ,cosθ+2,−2)，

设平面EBP的法向量为n=(a,b,c)，则n⋅EB=2b=0n⋅EP=asinθ+b(cosθ+2)−2c=0，

取a=2，则16.解：(1)以BC的中点O为原点，以1为单位长度，建立空间直角坐标系，如下图，由题意知，|AO|=3，

则A(3,0,0)，B(0,1,0)，C(0,−1,0)，A1(3,0,3)，B1(0,1,3)，C1(0,−1,3)；

(2)设AA1中点为点E，BC中点为点F17.解：(1)(i)因为圆E：x2+y2=4是集合A={(x,y)|ax+by=2}的包络圆，

所以圆心E(0,0)到直线ax+by−2=0的距离为2，整理得：

即|0−0−2|a2+b2=2，化简得a2+b2=1，

即a，b满足的关系式为a2+b2=1；

(ii)由a2+b2=1及3a+4b+t=0，

可得圆x2+y2=1与直线3x+4y+t=0有公共点，

所以|t|32+42≤1，解得−5≤t≤5，

所以t的取值范围是[−5,5]；

(2)设C(m,n)，由题意可知点C到直线xcosθ+(y+6)sinθ+62=0的距离为与θ无关的定值，

即d=|mcosθ+(n+6)sinθ+62|sin2θ+cos2θ，为与θ无关的定值，

所以m=0，n+6=0，故C(0,−6)，此时d=62，18.解：(1)设|AC|=m，|BC|=n，

易知|AC|+|BC|=2a，

即m+n=2a，且|AB|=23，

此时2a>23，

解则a>3，

由余弦定理得cosC=m2+n2−|AB|22mn=(m+n)2−2mn−122mn=2a2−6mn−1

≥2a2−6(m+n2)2−1=2a2−6a2−1=a2−6a2，

当且仅当m=n=a时，等号成立，

因为余弦函数y=cosx在[0,π]上为减函数，且C∈(0,π)，

所以当C取最大值时，cosC取最小值，

所以cos2π3=a2−6a2=−12，

解得a=2，

此时|AC|+|BC|=4>|AB|=23，

则曲线E是除去长轴端点的椭圆，且其长轴长为4，焦距为23，

所以b=a2−c2=4−3=1，

则动点C的轨迹E的方程为x24+y2=1(x≠±2)；

(2)易知D(−2,0)，

设直线MN的方程为x=my+1，m≠0，M(x1,y1)、N(x2,y2)，

联立x=my+1x2+4y219.证明：(1)当切线斜率存在时，

设直线y=kx+m与C1相切于点(x0,y0)，

联立y=kx+mx24+y2=1，消去y并整理得(4k2+1)x2+8kmx+4(m2−1)=0，

此时Δ=(8km)2−16(m2−1)(4k2+1)=0，