《电气测试技术第5版》 课件 2.0第2章 测量误差及数据处理

02December2024第2章

测量误差及数据处理

研究测量误差的目的是要在认识和掌握误差规律的基础上指导设计、制造和使用测量仪表。要解决一项测量任务，必须分析被测对象和被测量的特性，选用适当的测量仪表和测量方法，组成合理的测量系统，然后对测量结果进行数据处理和作出恰当的评价。所有这些都离不开误差理论的指导。02December2024第2章

测量误差及数据处理2.1误差来源及其分类2.2误差的表示方法2.3随机误差的估算2.4粗大误差的判断准则2.5系统误差及其减小方法2.6测量数据的处理2.7误差的合成与分配2.8最佳测量条件的确定02December2024教学目标掌握研究测量误差的目的。熟悉测量误差的来源及分类。掌握误差的表示方法、仪表的等级确定和测量仪表选用。掌握随机误差、粗大误差和系统误差的估算、判断和减小方法掌握测量数据的处理过程掌握常见的误差合成和分解掌握如何确定最佳测量条件02December20242.1误差来源及其分类

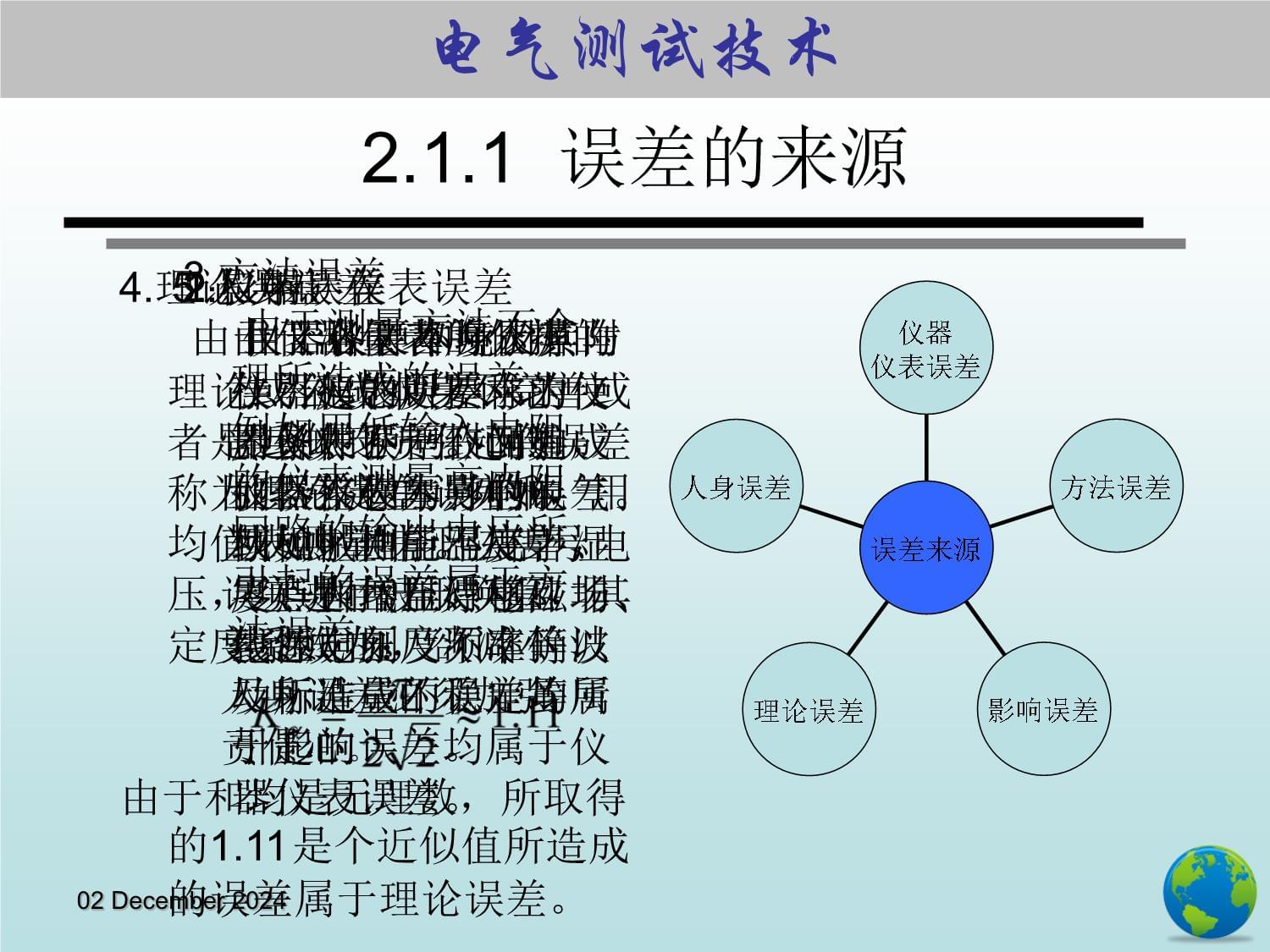
在科学实验和工程实践中，任何测量结果都含有误差。由于误差存在的必然性和普通性，人们只能将它控制到尽量低的程度而无法消除它。因此我们根据需要对误差的来源和测量误差的性质进行类，便于研究。2.1.1误差的来源

2.1.2误差的分类02December20242.1.1

误差的来源2.影响误差由于各种环境因素与仪器仪表所要求的使用条件不一致而造成的误差称为影响误差。例如，由于温度、湿度、大气压、电磁场、电源电压及频率等波动所造成的误差均属于影响误差。1.仪器、仪表误差

仪器仪表本身及其附件引起的误差称为仪器仪表误差。例如，仪器仪表本身的电气或机械性能不完善、零点和增益漂移、非线性、刻度不准确以及标准量不稳定等所引起的误差均属于仪器仪表误差。3.方法误差由于测量方法不合理所造成的误差。例如用低输入电阻的仪表测量高内阻回路的输出电压所引起的误差属于方法误差。4.理论误差由于仪器仪表所依据的理论或公式本身不完善或者是近似的所引起的误差称为理论误差。例如，用均值表测量非正弦信号电压，须进行波形换算，其定度系数为：由于和均是无理数，所取得的1.11是个近似值所造成的误差属于理论误差。

5.人身误差由于测量者的分辨力、视觉疲劳、习惯或缺乏责任心等因素引起的误差称为人身误差。人身误差是由于人为因素造成的，欲减小人身误差必须加强责任心。02December20242.1.2误差的分类根据误差的性质及其产生的原因，可将误差分为三类：

系统误差（简称系差）定义：在相同条件下多次测量同一量值时，误差的绝对值和符号保持不变，或者改变测量条件时，按一定规律变化的误差称为系统误差。前述仪器仪表误差、方法误差和理论误差均属于系统误差。系统误差是有规律性的误差。通过仔细分析和研究，产生系统误差的规律是可以掌握的。因此，可设法减小或消除系统误差。系统误差表征了测量结果的准确度，系统误差愈小，准确度念高，反之亦然。02December20242.1.2误差的分类随机误差

在相同条件下多次重复测量同一被测量，其误差的大小和符号均是无规律变化的误差称为随机误差。产生随机误差的原因是由于许多复杂的因素微小变化的总和引起的。例如，仪表内部某些元件的热噪声和散粒噪声、机械部件的间隙和摩擦、电源电压、频率和环境因素的频繁而无规律的变化等引起的误差均属随机误差。随机误差表征了测量结果的精密度，随机误差小，精密度高，反之，精密度低。02December2024服从正态分布规律的随机误差当测量次数足够多时，大多数随机误差是服从正态分布的。服从正态分布规律的随机误差具有下列特点（如下图所示）：单峰性绝对值小的误差比绝对值大的误差出现的概率大，在误差处，出现的概率最大。有界性绝对值大于某一数值的误差几乎不出现，故可认为随机误差有一定的界限。对称性大小相等符号相反的误差出现的概率大致相同。抵偿性正、负误差是相互抵消的，因此随机误差的代数和趋于或者等于零。服从正态分布规律的随机误差的特点：单锋性有界性对称性抵偿性02December2024粗大误差粗大误差（简称粗差）定义：在相同条件下多次测量同一被测量时，可能有某些测量值明显偏离了被测量的真正值所形成的误差称为粗大误差。前述的人身误差是产生粗差的原因之一。此外，由于测量条件的突然变化，例如电源电压突变、雷电、机械冲击等是造成粗差的客观原因。凡是被确认含有粗差的测量结果称为坏值。在测量数据处理时，所有坏值都必须剔除。02December20242.2误差的表示方法2.2.1测量误差的表示方法由于误差是客观存在的，因此在计量学上认为被测量的真正值是无法得到的。讨论被测量示值与真值的误差是没有应用意义的。实际值绝对误差、修正值被测量实际值取得的方法实际值相对误差02December2024实际值绝对误差定义：由测量所得之被测量的值与被测量实际值之差称为实际值绝对误差，记为。

（2-1）由此可见，为可正可负和有量纲的数值，其大小和符号分别表示测量值偏离被测量实际值的程度和方向。被测量实际值可用下列两种方法取得：用比所用仪表的精度等级高一级或数级的仪表的指示值作为被测量的实际值。在测量此数足够多时，仪表示值的算术平均值作为被测量的实际值。02December2024修正值定义：与绝对误差的数值相等而符号相反的量值称为修正值，用来表示，则： 修正值是通过检定（或校准）由上一级标准（或基准）以表格、曲线、公式或数字等形式给出的。因此，用修正值与仪表的示值相加，可算出被测量的实际值，即：

可见，用修正值可以减小测量误差，得到更接近于被测量真值的实际值。应该指出，使用修正值必须在仪表检定的有效期内。修正值本身也有误差。 02December2024实际值相对误差例2-3

测量两个电压，实际值，，仪表的示值分别为，。其绝对误差分别为：

很显然，虽然二者的绝对误差相同，但是二者测量的精确度却相差甚远，因此有必要引入相对误差的概念。定义：实际值绝对误差与被测量实际值之比的百分数称为实际值相对误差，即：02December20242.2.2仪器仪表误差的表示方法

误差是仪器仪表的重要质量指标。按有关规定，可用工作误差、固有误差、影响误差和稳定误差来表征仪器仪表的性能；也可以用基本误差和附加误差来表征仪器仪表的性能，本书采用后面一种表示方法。1.基本误差它是仪器仪表在标准条件下使用时所具有的误差。2.附加误差当仪表在使用中偏离了标准工作条件，除了基本误差外，还会产生附加误差。

02December2024基本误差定义：它是仪器仪表在标准条件下使用时所具有的误差。标准条件一般是指仪器仪表在标定刻度时所保持的工作条件。例如电源电压交流(220±5%)V，环境温度(20±5)℃；相对湿度(70±15)％；大气压(98.1±4.0)kPa等。对于相同的绝对误差，相对误差随被测量的增加而减小，相反，随的减小而增加，在整个测量范围内相对误差不是一个定值。因此，相对误差不能用于评价仪器仪表的精确度，也不便于用来划分仪器仪表的精度等级。为此提出最大满度相对误差称为最大引用误差的概念（在标准工作条件下）。02December2024满度相对误差与引用误差最大满度相对误差是仪表基本误差最大值与仪器仪表量程之比的百分数，即：最大引用误差是仪表的绝对误差最大值与仪器仪表量程之比的百分数，即：当仪表是在标准条件下使用的，则：02December2024仪表精度等级的确定仪表的精度等级（精确度等级）是指仪表在规定的工作条件下允许的最大相对百分误差。按国家标准规定，用最大引用误差来定义和划分仪器仪表的精度等级，将仪器仪表的精度等级分为：……

，

0.05，

0.1，0.25，0.35，0.5，1.0，1.5，2.5，4.0，5.0……（以前只有七种）当计算所得的与仪表精度等级的分档不等时，应取比稍大的精度等级值。仪表的精度等级通常以S来表示。例如，S=1.0，说明该表的最大引用误差不超过±1.0%。02December2024仪表的精确度等级仪表的精确度等级：指仪表在规定的工作条件下允许的最大相对百分误差。（把仪表允许的最大相对百分误差去掉“±”号和“％”号，便可用来确定其精度等级）所谓的0.5级仪表，表示该仪表允许的最大相对百分误差为±0.5％，以此类推。精度等级一般用一定的符号形式表示在仪表面板上（如右图所示）：也有以±0.2％FS

等形式写出精度等级数值小于等于0.05的仪表通常用来作为标准表，而工业用表的精度等级数值一般大于等于0.5。1.51.002December2024☆☆仪表的精确度等级☆☆例：某压力变送器测量范围为0～400kPa，在校验该变送器时测得的最大绝对误差为—5kPa，请确定该仪表的精度等级。解：先求最大相对百分误差去掉

和%为1.25，因此该变送器精度等级为1.5级。例：根据工艺要求选择一测量范围为0~40m3/h的流量计，要求测量误差不超过

0.5m3/h，请确定该仪表的精度等级。解：同样，先求最大相对百分误差因此该流量计必须选择1.0级的流量计。结论：工艺要求的允许误差≥仪表的允许误差

≥

校验所得到的相对百分误差

02December2024例：某被测温度信号在70～80℃范围内变化，工艺要求测量误差不超过±1％，现有两台温度测量仪表，精度等级均为0.5级，其中一台仪表的测量范围是0～100℃，另一台仪表的测量范围是0～200℃，试问这两台仪表能否满足上述测量要求。解：由题意可知，被测温度的允许最大绝对误差为：

|△max|＝70℃×1％＝0.7℃

测量范围为0～100℃的仪表的最大允许绝对误差为：

|△max|1＝100℃×0.5％＝0.5℃

测量范围为0～200℃的仪表的最大允许绝对误差为：

|△max|2＝200℃×0.5％＝1.0℃

根据上述计算，虽然两台仪表的精度等级均为0.5级，但只有测量范围是0～100℃的温度测量仪表才满足本题的测量要求。02December2024附加误差当仪表在使用中偏离了标准工作条件，除了基本误差外，还会产生附加误差。附加误差也用百分数表示。例如，仪表使用时温度超出(20±5)℃，则会产生温度附加误差；使用时电源电压超出(220±5%)V，则会产生电压附加误差。此外，还有频率附加误差，湿度附加误差，振动附加误差等等。在使用仪表时，附加误差和基本误差要合理综合，再估计出测量的总误差。

02December20242.2.3数字仪表误差的表示方法数字仪表的基本误差用下列两种方式表示：式中，为绝对误差；为误差的相对项系数；为被测量的指示值；为误差固定项的系数；为仪表的满度值。上述两种方式实质上是一致的，常用后一种，因较为方便。是用示值相对误差表示的，它与读数成正比，称为读数误差。它与仪表各单元电路的不稳定性有关。不随读数变化，一定时，它是个固定值，称为满度误差。它包括量化误差和零点误差等。02December20242.2.4一次直接测量时最大误差的估计在工程测量中，通常只做一次直接测量而取得测量结果，此时如何从仪器仪表的精度等级来确定测量误差呢？设只有基本误差的情况下，仪器仪表的最大绝对误差为：与示值之比，即为最大示值相对误差：02December2024一次直接测量时最大误差的估计可见，不仅与仪器仪表的精度有关，而且与满度值和示值之比值有关。示值大时，相对误差小。当时，。可见，仪器仪表给出的精度是相对误差的最小值。离开满度愈远，愈大。因此，当仪器仪表的精度等级已知时，示值愈接近满度值，测量示值的精度愈高。在使用正向刻度的模拟式仪表时，应尽量使指示值靠近满度值，至少应在左右。反之选择仪表量程时，应该使其满度值尽量接近被测量的数值，至少不应比被测值大得太多。02December2024例2-7

测量一个约80V的电压。现有二块电压表，一块量程为300V，0.5级，另一块量程100V，1.0级，问选择哪一块为好？解：根据式（2-9），求其最大相对误差。1）使用300V，0.5级电压表时2）使用100V，1.0级电压表时可见，用100V，1.0级电压表测量该电压时，精度比较高，故选用100V，1.0级电压表较好。02December2024例2-9

用一台4位的数字电压表的5V量程分别测量5V和0.1V电压，已知该仪表的基本误差为个字，求由于该表的基本误差引起的测量误差。解 ：①测量5V电压时的绝对误差。因为该表是4位，用5V量程时，±1个字相当于±0.001V，所以绝对误差为：

=±0.01%×5V±1个字=(±0.0005±0.001)V=±0.0015V

因此其示值相对误差为： ②测量0.1V电压时的绝对误差。

=±0.01%×0.1V±1个字

=(±0.00001±0.001)V≈±0.001V其示值相对误差为：02December2024结论可见，当不在接近满量程显示时，误差是很大的。因此，当测量小电压时，应当用较小的量程。同时还可看出，“±1个字”的误差对测量结果的影响也是比较大的，不可忽视。02December20242.3随机误差的估算2.3.1测量值的算术平均值与数学期望2.3.2标准差2.3.3随机误差的正态分布2.3.4贝塞尔公式2.3.5算术平均值标准差02December20242.3.1测量值的算术平均值与数学期望由同一测量者用同一仪器和方法，以同样的精细程度在短时间内对同一被测量进行多次重复测量，称为等精密度测量。设对被测量进行次等精密度测量，得测量值数列为：这里为随机变量，测量值的算术平均值为：也称为样本平均值。当测量次数时，样本平均值的极限称为测量值的数学期望：也称为总体平均值。02December2024随机误差是精密度的反映，表征了各次测量值的分散程度，故随机误差为： ，即而系统误差是准确度的反映，则系统误差为： ，即式中，是被测量真值。真值绝对误差是测量示值与真值之差：由上式可见，绝对误差等于随机误差和系统误差的代数和。若系差和粗差等于零，故则：02December2024随机误差的算术平均值为：由上式可知，当时，则

由此可见，当时，随机误差的算术平均值为零。对于有限次等精密度测量，当足够多时，可近似认为。由上式得：

由此可见，若仅存在随机误差，可用多次测量的算术平均值作为最后测量结果。（常在实验里用到）

02December20242.3.2标准差测量值的算术平均值是被测量的最可信赖值。但是仅知道测量值的算术平均值仍无法知道测量值的分散程度。被测量的分散程度可以用测量值数列的标准差来表示。其定义为：当时，随机误差的平方的算术平均值再开平方后，只取正值，即标准差是表征精密度的重要参数。小表示测量值集中；

大，表示测量分散。取平方的目的是，不论是正是负，其平方总是正的，其平方和不会等于零，给计算带来方便。02December20242.3.3随机误差的正态分布

由概述论中的讨论可知，测量中随机误差的分布和在影响下的测量数据的分布大多数是服从正态分布的。服从正态分布的随机误差，其概率密度函数为：

式中，为随机误差；为标准差。与的曲线见图2-1。由图可见，标准差一经确定，就是的单值函数。

图2-1随机误差的正态分布曲线02December20242.3.3随机误差的正态分布图2-2示出了三个不同的对应的三条正态分布曲线。由图可见，愈小，曲线愈高愈陡，小误差出现的概率愈大，表示测量值集中，精密度高；反之，愈大，曲线平坦，测量值分散，精密度低。图2-2标准差的意义02December20242.3.4贝塞尔公式

在实际测量中，测量次数不可能无穷大。当测量次数为有限次时，可用剩余误差来计算标准差，同时用标准差的估计值代替。在有限次测量中，标准差估计值可用贝塞尔公式计算，即：式中，（）称为自由度，常用表示，。

由上式可见，当时，值不定，故仅做一次测量的数据是不可靠的。

02December20242.3.5算术平均值标准差在有限次等精密度测量中，以测量值的算术平均值作为测量结果。如果在相同条件下对同一量值作组，每一组作次测量，通过计算可得到个算术平均值。由于随机误差的存在，这个算术平均值并不相同，而围绕着真值有一定的分散性。这说明了算术平均值还存在着误差。当需要更精密考虑时，可用算术平均值的标准差来评定测量结果的分散程度。算术平均值标准差与标准差估计值的关系为：

02December2024算术平均值标准差由上式可见，随的增加而减小，测量次数愈多，测量结果的精密度愈高。但由于与成反比，精密度的提高随的增加而越来越慢。一般取次即可。不能单靠增加来减小，而应该在增加的同时，设法减小。这就意味着要改善测量方法，采用精确度等级较高的仪器仪表，才能进一步提高测量的精密度。02December20242.4粗大误差的判断准则2.4.1置信概率与置信区间2.4.2有限次测量的置信度2.4.3随机不确定度与坏值剔除02December20242.4.1置信概率与置信区间由概率积分可知，随机误差的正态分布曲线所包含的全部面积相当于全部误差出现的概率，对式（2-18）从-∞到+∞积分，并令其等于1，即：对式（2-18）从到积分，便可得误差出现的概率：将积分变换成，设，则，故上式变为：式中，称为概率积分，与的关系见表2-1。

02December2024由写出随机误差的表达式，并取绝对值，即： 可得出超出的概率为：

由表2-1查出不同的对应的值，便可由式算出，见表2-2，表2-2中，为测量次数。图2-3置信概率与置信区间的关系02December2024表2-1正态分布下的置信概率数值表0.500.600.700.800.901.001.101.201.301.400.19150.22570.25800.28810.31590.34130.36430.38490.40320.41921.501.601.701.801.902.002.102.202.302.400.43320.44520.45540.46410.47130.47720.48210.48610.48930.49182.502.602.702.802.903.003.203.403.804.000.49380.49530.49650.49740.49810.498650.499310.499660.4999280.49996802December20241.001.962.002.583.001.001.962.002.583.000.34130.47500.47720.49500.498650.31740.05000.04560.01000.002732022100370表2-2正态分布的置信系数总而言之，不超出的概率为，可由式（2-24）求得：02December2024置信区间

取不同值时，随机误差出现的概率为：当时， 时， 时，上述结果表明，对于正态分布规律的随机误差，不超出的随机误差出现的概率为95.44%；不超出的随机误差出现的概率为99.73%。上述用于描述测量结果的误差处于某一范围内的可靠程度的量称为置信程度或者置信概率。所选择的极限误差范围称为置信区间。02December20242.4.2有限次测量的置信度图2-4所示的置信概率与置信区间的关系，是在测量次数足够多，误差服从正态分布，以标准差为条件得出的结论。当测量次数足够多（）时，应用这一结论是合适的。因为随机误差的分布接近正态分布。若测量次数较小（），随机误差的分布曲线与正态分布曲线差别较大，而服从分布（也称学生分布），正态分布曲线与分布曲线的不同见图2-4。为区别于正态分布，分布用置信系数表示。自由度、置信概率与置信系数的关系见表2-3。若已知和置信概率，可由表2-3查出置信系数。02December202495%99%95%99%123456789101214161812.714.303.182.782.572.452.362.312.262.232.182.142.122.1063.669.925.844.604.033.713.503.363.253.173.052.982.922.88202224262830405060708090100∞2.092.072.062.062.052.042.022.012.001.991.991.991.981.962.852.822.802.782.762.752.702.682.662.652.642.632.632.58表2-3学生分布的置信系数

02December20242.4.3随机不确定度与坏值剔除由表2-2可见，若取置信系数，在22个随机误差中，至多仅有一个的误差大于；若取，在370个误差中，至多仅有一个误差大于。在实际测量中，可以认为大于的误差出现的可能性极小，所以通常把大于的误差称为极限误差或随机不确定度，用表示

或用估计值这个数值说明测量结果在数学期望附近某一确定范围内的可能性有多大，由测量值的分散程度来决定，所以用标准差的若干倍来表示。02December2024莱特准则根据上述理由，在测量数据中，如果出现大于的剩余误差，可以认为该次测量值为坏值，应予剔除，即：

上式称为莱特准则（亦称为准则）。在测量次数足够多（）时，按莱特准则剔除坏值是客观的和合理的。但是，若测量次数较少（），按莱特准则剔除坏值就不一定可靠，这时应采用格拉布斯（Grubss）准则。02December2024格拉布斯准则在等精密度测量数据中，若有剩余误差的绝对值满足下式：

则认为与该相对应的测量数据是坏值，应予剔除。式中是格拉布斯系数，见表2-4。算术平均值的不确定度可以表示为：当足够大时 当较小时 或者 剔除坏值后，对剩余的测量数据重新计算算术平均值和标准估计值，再次作判断，直到测量数据中无坏值为止。

02December20242.5系统误差及其减小方法如前所述绝对误差是系统误差和随机误差的代数和，即。此式说明测量结果的精确度不仅取决于随机误差，也取决于系统误差。由于系差不具有抵偿性，不能用求算术平均值的方法加以消除。但是，系差是有规律性的误差，经过仔细的分析和研究，其产生的规律是可以掌握的，因此可以采取一些技术措施削弱或消除其对测量结果的精确度的影响。2.5.1系统误差的分类2.5.2系统误差的判断2.5.3减小系统误差的方法02December20242.5.1系统误差的分类按照系差变化的征性，可将系差分为两种类型。恒值系统误差在测量过程中误差的大小和符号是不变的误差称为恒值系差。例如，仪器仪表的基本误差、仪表的零点偏高或低、标尺刻度不准确等均属于恒值系差，见图2-5曲线a。变值系统误差误差的绝对值和符号按照一定规律变化的误差称为变值系差。线性系统误差在测量过程中误差的数值随差时间线性增加或者减小的误差称为线性系差。例如由于晶体管老化过程引起放大倍数下降引起的误差；标准电池的电动势随时间而减小引起的误差等均属此类系误。见图2-5曲线b。周期性变化的系统误差在测量过程中误差值作周期性变化，见图2-5曲线c。复杂变化的系统误差在测量过程中误差的变化规律很复杂，见图2-5曲线d。通常它是由几个影响因素同时变化引起的。图2-5系统误差的特征02December20242.5.2系统误差的判断由于产生系差的原因很多，所以发现它或判断它的方法也很多，这里仅介绍几种常用的判断方法。实验对比法改变测量条件、测量仪器仪表或测量方法进行重复测量，然后将测量结果进行对比，从而发现系差。剩余误差观察法用仪器仪表对某一被测量进行一系列等精密度测量，得示值，然后求算术平均值，并求出各示值的剩余误差，最后将剩余误差数列按测量先后制成表格或画成曲线进行观察，从而判断是否存在系差。02December2024马利科夫判据马利科夫判据该判据用于判断是否存在线性系差。首先将测量数据按测量先后排列起来，分别求剩余误差。把剩余误差数列分为前后两组，分别求前后两组的代数和，然后求前后两组代数和之差：当为偶数时，当为奇数时，如果满足：则认为不存在线性系差。如果满足：则认为存在线性系差。式中是最大剩余误差。02December2024阿卑—赫梅特判据阿卑—赫梅特判据该判据用于判断是否存在周期性系差。首先按测量数据的测量先后求剩余误差列。然后用下式判断：若上式成立，则认为存在周期性系差，否则不存在周期性系差。对于存在变值系差的测量数据，原则上应舍去不用。但是，若明显小于测量允许的误差范围或者仪器仪表的基本误差，也可以考虑使用。02December20242.5.3减小系统误差的方法对于测量者，善于找出产生系差的原因并采取有效措施以减小误差是极为重要的。它与被测对象、测量方法、仪器仪表的选择以及测量人员的实践经验密切有关。下面介绍几种常用的减小系差的方法。从产生系差的原因采取措施定期校正减小缓变系差用加修正值方法减小系差零位测量法微差法替代法02December2024从产生系差的原因采取措施接受一项测量任务后，首先要研究被测对象的特性，选择适当的测量方法和测量仪表、所用仪表的精度等级和量程上限；测量工作环境（如温度、湿度、大气压、交流电源电压、频率、振动、电磁场干扰等）是否符合仪表的标准工作条件。必要时可采用稳压、稳频、恒温、散热、防振和屏蔽接地措施。测量者应提高测量技术水平，增强责任心，克服主观原因所造成的误差。为避免读数或记录出错，可用数字仪表代替指针式仪表，用自动打印代替人工抄写等。总之，在测量工作开始前，尽量消除产生误差的根源，从而减小系差的影响。02December2024定期校正减小缓变系差缓变系差的特点是随时间平稳变化。例如，仪表的零点和灵敏度过一段时间后可能会发生变化，见图2-6。原来仪表的输入输出特性见图2-6直线1，经过一段时间后可能变成直线2。显然仪表的零点和灵敏度（或满度值）已发生变化、产生了系差。应调整仪表的零点和满度值机构使直线2回复至直线1，恢复仪表原来的输入输出特性，从而减小系差。为了不断消除仪表的缓变（或线性变化）的误差，应定期对仪表进行校正，校正周期愈短，缓变误差愈小。

图2-6校正仪表零点和灵敏度02December2024微差法设标准量为，被测量为，微差为，则微差法的绝对误差为： 式中，为标准量的绝对误差；为测量的绝对误差。相对误差为：

因为。故，并令，得：

式中，为标准量的相对误差，即为标准量的精度等级；为测量微差的示值相对误差。由于标准量的精度等级很高，故上式第一项误差很小；第二项是两个小于1的数之乘积也很小。所以用微差法可以减小系差。02December2024

设标准电压，级。已知微差，用，级电压表测量。求测量的相对误差。解：测量的相对误差为：

测量的相对误差为：

可见，测量误差主要取决于标准量的精确度，而仪表引起的测量误差仅为0.06%。在测量微差时误差达±3.0%，但它在总误差中仅占0.06%。用级仪表，可达到0.06%的精度。

02December2024替代法替代法是在测量过程中将被测量以等值的标准量来替换。替换时，要使仪器的工作状态前后不变，这样就能消除由仪器产生的恒值系差。可见，测量的误差与桥路参数的精度无关，仅取决于标准电阻的精度，因此可减小系差。

图2-7替代法减小系差02December20242.6测量数据的处理

测量数据的处理是指从原始的测量数据中经过加工、整理求出被测量的最佳估计值，并计算其精确度。2.6.1测量数据的舍入法则2.6.2有效数字的位数2.6.3有效数字的运算规则2.6.4有效数字位数的确定2.6.5等精密度测量结果的处理步骤02December20242.6.1测量数据的舍入法则由于测量数据是由0，1，2，3，…，9十个数组成的近似数，因此在进行数据处理时会遇到数据的舍入问题。通常的“四舍五入”规则中，对5只入不舍是不合理的，它也应当有舍有入。所以在测量技术中规定：“小于5舍，大于5入，等于5时采取偶数法则”。也就是说，保留数字末位为位，第位大于5，第位数字加1；第位小于5，第位数字不变；若第位恰好是5，则将第为凑成偶数，即第位为奇数时，第位加1，第位为偶数时，则第位不变。例2-10将下列数字保留三位：

12.34→12.3（4<5）

12.36→12.4（6>5）

12.35→12.4（因第三位是3为奇数，5入）

12.45→12.4（因第三位是4为偶数，5舍）当舍入足够多时，舍和入的概率相同，从而舍入误差基本抵消，又考虑到末位是偶数容易被除尽，减小计算误差。由此可见，每个数据经舍入后，末位是欠准数字，末位以前的数字是准确数字。其舍入误差不会大于末位单位的一半，这是最大舍入误差，故称该舍入法则为“0.5”误差法则。02December20242.6.2有效数字的位数所谓有效数字的位数，是指在一个数值中，从第一个非零的数算起，到最末一位数为止，都叫有效数字的位数。例如，0.27是两位有效数字；10.30和2.102都是四位有效数字。可见，数字“0”在一个数值中，可能是有效数字，也可能不是有效数字。02December20242.6.3有效数字的运算规则在数据处理中，常需要对一些精度不相等的数进行四则运算。为了使计算简单准确，可首先将参加运算的各个数，以精度最差的一个为基准进行舍入处理（也可多保留一位欠准数字），计算结果也按精度最差的那个数为基准作舍入处理（也可以多保留一位或两位欠准数字）。这样使计算简便准确。02December20242.6.4有效数字位数的确定确定有效数字位数的标准是误差。并非写得越多越好，多写位数，就夸大了测量的精确度，少写位数就会带来附加误差。测量结果有效数字处理原则是：由测量精确度来确定有效数据的位数，但允许多保留一位欠准数字，与误差的大小相对应，再根据舍入法则将有效位以后的数字舍去。02December2024例2.12

用一块=100V，s＝0.5级电压表进行测量，其示值为85.35V，试确定有效数字位数。解：该量程的最大误差为：可见示值范围为84.85~85.85V，因为误差是±0.5V，根据“0.5”误差法则，此数据的末位应是整数，所以测量结果应写成两位有效数字，根据舍入法则，示值末尾的0.35<0.5，因此，不标注误差的报告应写成85V。由上可见，测量结果的有效数字反映了测量的精确度。

有效数字的位数与小数点的位置和所用单位都无关，而只由误差的大小所决定，这是应该十分明确的。

02December20242.6.5等精密度测量结果的处理步骤对某一被测量进行等密度测量时，其测量值可能同时含有随机误差、系统误差和粗大误差。为了合理估算其测量结果，写出正确的测量报告，必须对测量数据进行分析和处理。数据处理的基本步骤如下：用修正值等方法，减小恒值系统误差的影响。求算术平均值式中，是指可能含有粗差在内的平均值。02December2024等精密度测量结果的处理步骤求剩余误差，并验算的代数和是否等于零，从而验算计算平均值的正确性。若的代数和约等于零，说明的计算是正确的；否则说明计算时有错，要重新计算。求标准差的估计值。利用贝赛尔公式02December2024等精密度测量结果的处理步骤判断粗差，剔除坏值。当足够大时，随机不确定度为：当较少时，利用格拉布斯准则： 若有，则认为对应的测量值是坏值，应予剔除。剔除坏值后，利用剩下的数据再来求，剩余误差，标准差和随机不确定度，并再次判断粗差和剔除坏值，知道测量数据没有坏值为止，然后继续往下计算。02December2024判断有无变值系统误差马利科夫判据当为偶数时，当为奇数时，上两式中的必须是无坏值时所计算得到的剩余误差。若，则认为存在线性系差。含有线性系差的数据原则上不能使用应重新作等精密度测量）利用阿卑－赫梅特判据判断有无周期性系差。若上式成立则认为存在周期性系差。是无坏值时的标准差估计值。含有周期性系差的数据也不能使用。

02December2024求算术平均值标准差估计值求算术平均值的不确定度当较小时或 当较大时 给出测量结果的表达式或报告值。对于技术测量，需要指明不确定度时，可表示为：若不指明不确定度，可用代表。

必须指出，上述计算所用数据和计算所得各个值均是在无坏值情况下的计算结果。在上述计算过程中，也应当考虑有效数字的位数，可先化整然后再计算，使计算简化。为避免累积误差，在化整和结果中可保留两位欠准数字。但最后结果要与误差相对应。02December2024例2.13对某一电压进行16次等精密度测量。测量数据中已计入修正值，具体数值见表（单位为V）。要求给出包括误差（即不确定度）在内的测量结果表达式。1205.300.000.099205.01-0.29-0.202204.94-0.36-0.2710204.70-0.60-0.513205.63+0.330.4211205.560.260.354205.24-0.060.0312205.350.050.145206.65+1.35－13205.21-0.090.006204.97-0.33-0.2414205.19-0.11-0.027205.36+0.060.1515205.21-0.090.008205.16-0.14-0.0516205.320.020.1102December2024解：1）计算算术平均值2）计算剩余误差各列于表2-5中第三列。然后求的代数和说明计算算术平均值是正确的。3）计算标准差估计值。利用贝赛尔公式02December20244）判断粗差。求随机不确定度，因为次，比较少，采用格拉布斯准则。取，查表2-4，得格拉布斯系数，则 查表2-5，可知为最大，大于，所以测量值是坏值，予以剔除。此外没有大于的，暂定坏值只有一个，剩下数据只有15个。5）重新计算，和值

计算剩余误差，列于表2-5的第四列。计算标准差估计值，再查表2-4，得，算出

再判断坏值。查表2-5知。说明所剩数据中没有坏值。02December20246）判断有无变值系差①马利科夫判据判断是否有线性系差

查表2-5知，可见，不存在线性系统误差。②利用阿卑－赫梅特判据判断有无周期性系差。 而 可见，故不存在周期性系差。

02December20247）利用计算算术平均值标准差的估计值

8）计算不确定度。较少，，取，查表2-3，得，则 9）给出测量结果的表达式（报告值）。由值可以看出，测量结果只能精确到十分位，从而得出被测量

这一结果表明，虽然被测电压的真值不知道，但可以用经过数据处理后的算术平均值代表它。在这个数值中含有随机误差，其标准差为0.06V，但无论如何不可能超过0.1V。

02December20242.7误差的合成与分配2.7.1概述2.7.2常用函数的合成误差2.7.3系统误差的合成2.7.4系统误差的分配02December20242.7.1概述测量方法分为：直接测量、间接测量和组合测量；前面课程涉及的误差计算都是在直接测量的基础上讨论的。对间接测量的误差又应该如何计算？02December2024间接测量的误差计算问题？又如测量标准电阻的电阻率：需测量标准电阻的电阻值、横截面积和长度。如果已知、和，如何计算？110米跨栏12秒88S1–S2刘翔已知如何求?02December2024误差的合成与分配误差的合成

已知被测量与各个参数的函数关系以及各个参数测量值的分项误差，求被测量的总误差称为误差的合成。例如研究一台仪表各局部环节的系统误差与整台仪表系统误差之间的关系；间接测量时，被测量误差与各测量值误差之间的关系（刘翔的跨栏时间测量）等。误差的分配

已知总误差及其与各测量值之间的函数关系，将总误差合理地分配给各测量值称为误差分配。例如在设计一台测量仪表时，应当怎样合理分配各环节和各元件的系统误差。02December2024误差传递公式若要进行误差的合成与误差的分配，首先必须知道误差的传递公式。那么误差传递公式又是如何得出的？设被测量与各测量值之间的函数关系为，测量值各自有独立的绝对误差，则有绝对误差。与之间的关系为：上式是绝对误差的传递公式。是误差传递系数。02December2024绝对误差与相对误差前式表明，总误差是各分项误差与其传递系数的代数和。即对函数表达式求全微分，然后求其代数和便可得到的绝对误差。前式两边也分别除以，便过得相对误差的传递公式：由上式可见，对函数两边分别取自然对数，再求全微分，然后求代数和便可得到的合成相对误差。02December20242.7.2常用函数的合成误差积函数的合成误差（功率测量）设，是积函数。对求全微分得其绝对误差为：

若要求其相对误差，可对取对数再求全微分，即

上式说明，由积函数的合成相对误差等于各分项误差之和。当和分别有“±”号时，从最大误差出发，总误差应等于各分项误差之绝对值和。即

02December2024例2-14已知电阻上的电压和电流的误差分别为±2.0%和±1.5%，求电阻耗散功率的相对误差。 解：电阻耗散功率，此为积函数。根据式（2-41）得：如果已知电阻和电流的误差为±2.0%和±1.5%，则

02December20242.7.2常用函数的合成误差2.商函数的合成误差已知为商函数。对求全微分可得其绝对误差为：对取对数得，然后微分得的相对误差为：

可见，商函数的合成相对误差是各分项相对误差之差。但由于和往往前面有“±”号，从最大误差出发，仍取各分项误差的绝对值相加，即：与积函数一样02December2024例2-15已知放大电路晶体管集电极电阻，利用测量上的压降,然后间接测得集电极电。已知测量电压的误差是±1.5%，电阻的误差是±2.0%，求测量电流的误差。解：已知是商函数。根据式（2-44）可得测量电流的误差为：

02December20242.7.2常用函数的合成误差3.幂函数的合成误差设，可见是幂函数。对取对数得：

然后微分，得的合成误差

式中，、和为影响系数。02December2024例2-16电流流过电阻，发热量。已知，，，求是多少？解：由于，和的前面均有“±”号，从最大误差出发，仍取各项误差的绝对值相加。 由式（2-45）可得

由此例说明，因为测量电流的影响系数为2，而的误差占了总合成误差的近80%，因此，选择合成函数时应尽量避免影响系数大的函数。02December20242.7.2常用函数的合成误差4.和差函数的合成误差设，左式求全微分得绝对误差

若各分项误差的符号不能预先确定时，从最大误差出发，仍取绝对值相加，即

相对误差

02December20244.和差函数的合成误差①设是和函数，则

②设是差函数。同理得：

当和的符号为未知时，上两式仍需取绝对值相加。 由式（2-49）可见，当和比较接近时，其合成误差比较大，所以尽量不选择差函数。02December2024例2-17

用三瓦特表法测量三相交流电路中的功率，各仪表的示值分别为、和，设三仪表的相对误差相等为。求总功率的相对误差为多少？ 解：三相交流电路的总功率等于

由式（2-48）可知，总功率的误差为：

可见，若测量三相功率的各功率表相对误差相同，三相电路总功率的相对误差等于任一相功率的误差。02December2024例2-18

用指针式频率计测量放大电路的频带宽度，仪器的级。测量值，。求频带宽度的合成误差。 解：测量的相对误差为：

测量的相对误差为：

已知频带宽度 由于和的符号均为未知，代入式（2-49），并取绝对值相加，得：

02December20245.和差积商函数的误差例2-19两只电阻和联，求并联后电阻的总误差。解：并联后总电阻是和差积商函数。根据误差传递公式（2-37）可以得出：

则

即

当时，则。表明相对误差相同的电阻并联后总电阻的相对误差与单个电阻的相对误差相同。其相对误差为：02December20242.7.3系统误差的合成1.已定系统误差的合成对于已定系差，由于误差的大小、符号和函数关系均为已知，故可直接由误差传递公式（2-37）进行合成。因为，如果则可对各分项误差采用代数和法进行合成。即：

而相对误差为：

02December2024例2-20

有五个1000Ω电阻串联，若各电阻的系统误差分别为：，，，，。求总电阻的绝对误差和相对误差。解：

其相对误差为：

02December20242.系统不确定度的合成

对于未定系统误差，由于往往只知道其误差极限而不知道其确切的大小和符号，因此对它的合成方法视具体情况而定。通常可用下列两种方法。（1）绝对值和法各分项误差取绝对值，然后求和。用式子表示为：①绝对系统不确定度

②相对系统不确定度

一般情况下，02December2024

例2-21：用二功率表法测量三相三线制电路中的总功率。设两功率表的级，，。它们的读数分别为，。求测量总功率的系统不确定度。解：总功为。根据式（2-53）和仪表精度等级的定义，可求出测量和的局部系统不确定度

由此可得测量总功率的系统不确定度

其相对系统不确定度为

02December2024例2-22

用晶体管毫伏表，级测量，的电压。已知在20Hz～1MHz内频率附加误差。求相对系统不确定度。解：仪表的基本误差为：

相对系统不确定度为：

当各分项误差较少时，采用绝对值和法是比较保险的，因为在这种情况下，各分项误差在相同方向相叠加的机会较大。但是，当各分项误差