2013年全国各地中考数学试题1-15(共50套)

2013年沈阳中考数学试卷

考试时间：120分钟,试卷满分150分,

参考公式：参考公式：抛物线》=狈2+法+。的顶点坐标是12竺匚£）.

对称轴是直线x=__L,

2a

注意事项2

1.答题前，考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的姓名、准考

证号；

2.考生须在答题卡上作答，不能在本试题卷上作答，答在本试题卷上无效；

3.考试结束，将本试题卷和答题卡一并交回；.

4.本试题卷包括八道大题，25道小题，共6页.如缺页、印刷不清，考生须声明，否则后

果自负.

一、选择题（下列各题的备选答案中，只有一个答案是正确的，每小题3分，共24分）

1.2013年第一季度，沈阳.市公共财政预算收入完成196亿元（数据来源：4月16日《沈

阳日报》），讲196亿用科学记数法表示为（）

A.1.96X108*B.19.6xl08C.1.96x10'°D.19.6xlO,0

2右图是一个几何体的三视图,这个几何体的名称是（）

主视图左视图

A圆柱体B.三棱锥C.球体D.圆锥体

第二题图

3下面计算一定正确的是（)俯视图

Ab、/=2优B.(—3pg)-=-9p-q-

c5/-3/-15/D.D=b，

4如果机=V7-i,那么m的取值范围是（)

A0</??<1B.\<m<2C.2<m<3D.3<<4

5下列事件中，是不可能事件的是（)

A买一张电影票，座位号是奇数B.射击运动员射击一次，命中9环.

C明天会下雨.D.度量三角形的内角和，结果是360°

23

6计算------+------I的结果是（)

x-11-x

1B.,55

AC.D.

x-11-xX—11-x

函数y=x—1与函数），=工的图象可能是（）

7、在同一平面直角坐标系中,

X

ABCD

8.如图,AA8C中，AE交BC于点D,ZC=ZE,AD=4,BC=8,BD:DC=5：3,则DE的长

等于（）

“2015-16r1

A.—Bn.—C.—D.一

3434

二、填空题（每小题4分，共32分）

9.分解因式：3“2+6a+3=

10.一组数据2,4,x,-1的平均数为3,则x的值是=.

11.在平面直角坐标系中，点M（-3,2）关于原点的对称点的坐标是.

12.若关于x的一元二次方程f+4x-。=0有两个不相等的实数根，则a

的取值方位是.

13.如果x=l时，代数式2〃/+3历c+4的值是5,那么x=-1时，代数式

2ax2+3bx+4的值.

14.如图，点A、B、C、D都在。0上，N4BC=90°,AD=3,CD=2,则。0的第14题图

直径的长是.

15.有一组等式

12+22+32=32,22+32+62=72,32+42+122=132,42+52+202=212....，请.观察它

们的构成规律，用你发现的规律写出第8个等式为

16.已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距

离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是

三、解答题（第17、18小题各8分，第19小题10分.共26分）

18.一家食品公司将一种新研发的食品免费送给一些人品尝，并让每个人按A（不喜欢）、

B（一般）、C（比较喜欢）、D（非常喜欢）四个等级对该食品进行评价，图①和图②是

该公司采集数据后，绘制的两幅不完整的统计图。

笫18题图①

请你根据以上统计图提供的信息，回答,下列问题；

(1)本次调查的人数为人；

(2)图①中，a=,C等级所占的圆心角的度数为度;

(3)请直接在答题卡中不全条形统计图。

19.如图，A4BC中，AB=BC,BE_LAC于点E,AD_LBC于点D,NBA。=45。，AD与BE交

于点F,连接CE,

(1)求证:BF=2AE

(2)若CD=0.,求AD的长。

第19题图

四、(每小题10分，共20分)

20.在一个不透明的盒子中放有三张卡片，每张卡片上写有意个实数，分别为3,6,

JI+6。(卡片除了实数不同外，其余均相同)

(1)从盒子中随机抽取一张卡片，请草篆写出卡片上的实数是3的概率；

(2)先从盒子中随机抽取一张卡片，将卡片上的实数作为被减数；卡片不放回，再随机抽

取一张卡片，将卡片上的实数作为减数，请

你用列表法或树状图(树形图)法，求出两次抽取的卡片上的实数之差为有理数的概率。

21.身高1.65米的兵兵在建筑物前放风筝，风筝不小心挂在了树匕在如图所示的平面图

形中，矩形CDEF代.表建筑物，兵兵位于建筑物前点B处，风筝挂在建筑物上方的树枝点G

处(点G在FE的延长线上)，经测量，兵兵与建筑物的距离BC=5米，建筑物底部宽FC=7

米，风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上，点A据地面的高

度AB=1.4米，风筝线与水平线夹角为37。。

(1)求风筝据地面的告诉GF；

(2)在建筑物后面有长5米的梯子MN,梯脚M在距离3米处固定摆放，通过计算说明；若

兵兵充分利用梯子和一根5米长的竹*竿能否触到挂在树上的风筝？

第21题图

五、(本趣10分)

22.如图，0C平分NMON,点A在射线0C上，以点A为圆心，半径为2的OA与0M相切

于点B,连接BA并延长交。A于点D,交0N于点E。

(1)求证：0N是。A的切线；

(2)若NMON==60°,求图中阴影部分的面积。(结果保留”)

第22题图

六、（本题12分）

23.某市对火车站进行了大规模的改建，改建后的火车站除原有的普通售票窗口外，新增了

自动打印车票的无人售票窗口，某日，从早上8点开始到上午11点，每个普通售票窗口售

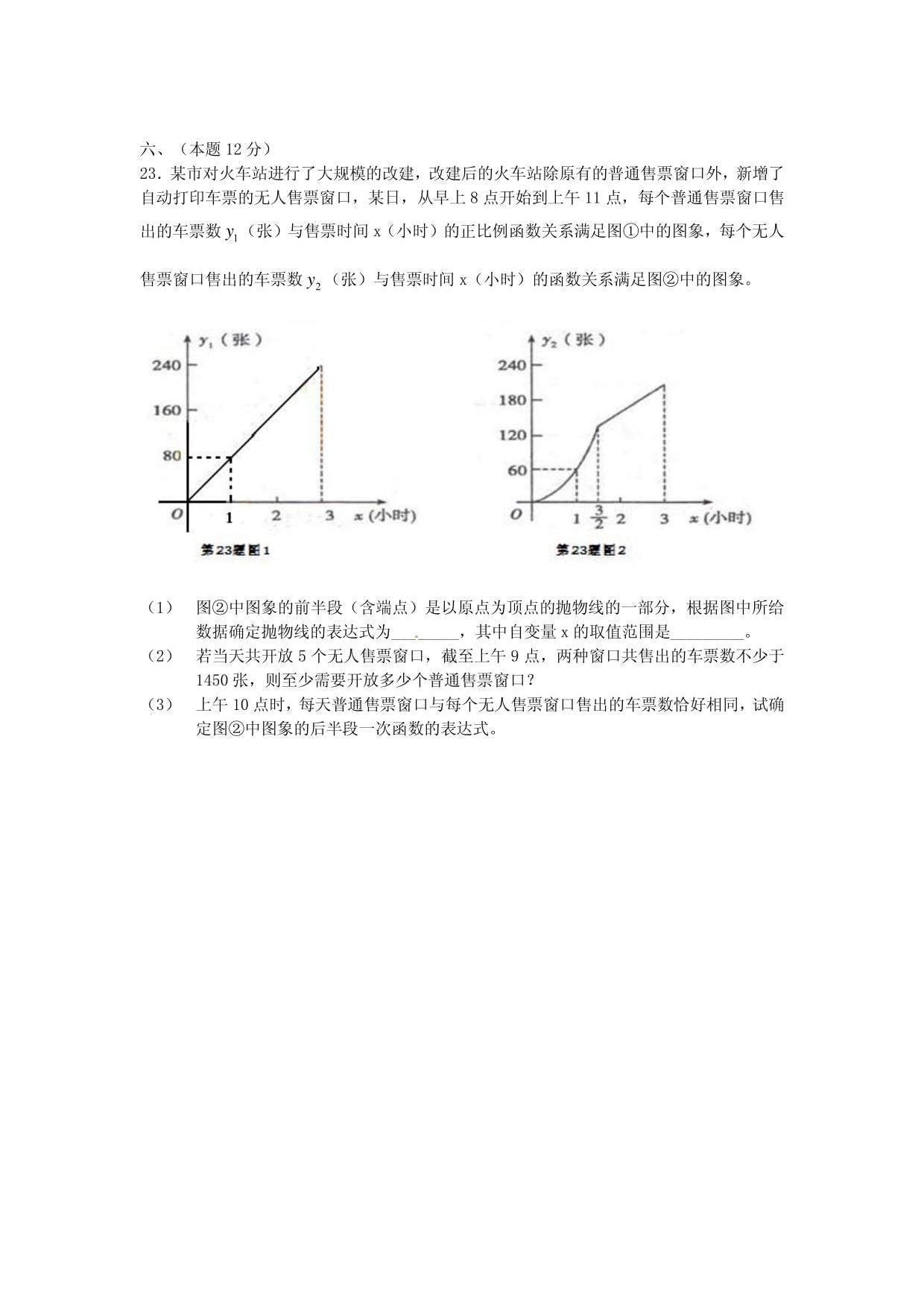
出的车票数/（张）与售票时间x（小时）的正比例函数关系满足图①中的图象，每个无人

售票窗口售出的车票数当（张）与售票时间x（小时）的函数关系满足图②中的图象。

（1）图②中图象的前半段（含端点）是以原点为顶点的抛物线的一部分，根据图中所给

数据确定抛物线的表达式为,其中自变量x的取值范围是。

（2）若当天共开放5个无人售票窗口，截至上午9点，两种窗口共售出的车票数不少于

1450张，则至少需要开放多少个普通售票窗口？

（3）上午10点时，每天普通售票窗口与每个无人售票窗口售出的车票数恰好相同，试确

定图②中图象的后半段一次函数的表达式。

七、(本题12分)

24.定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”

性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等，

理解：如图①，在A48C中，CD是AB边上的中线，那么AACO和ABC。是“友好三角

形”，并且SM°=S&BCD°

应用：如图②，在矩形ABCD中，AB=4,BC=6,点E在AD上，点F在BC上，AE=BF,AE

与BE交于点0,

(1)求证：A4O8和A4OE是''友好三角形”；

(2)连接0D,若A4OE和AOOE是“友好三角形”，求四边形CDOF的面积，

探究：在A4BC中，ZA=30°,AB=4,点D在线段AB上，连接CD,A4CO和ABC。是

“友好三角形”，将A4CO沿CD所在直线翻折，得到A4'CZ)与重合部分的面积等

于MBC面积的工，请直接写出M5C的面积。

4,•

BC

第24题图②

八、（本题14分）

o3

25.如图，在平面直角坐标系中，抛物线y=\—》2+法+，经过点AI],0）和点B（1,

2夜），与x轴的另一个交点为C,

（1）求抛物线的表达式；

（2）点D在对称轴的右侧，x轴上方的抛物线上，且/BD4=ND4C,求点D的坐标；

（3）在（2）的条件下，连接BD,交抛物线对称轴于点E,连接AE

①判断四边形0AEB的形状，并说明理由；

②点F是0B的中点，点M是直线BD上的一个动点.，且点M与点B不重合，当

NBMF=-ZMFO,请直接写出线段BM的长

3•,

第25题图

数学试:麴

一、选择题（每小题3分，共24分）

1C2.A3.C4.B5.D6B7.C8,B

二、填空题（每小悲4分，共32分）

9.3（a+1）210.711.（3,-2）12.a<413.3

14.VT315.8?+92+722=73216.1,7

三、解答题（第17、18小题各8分，第19小题1。分，共26分）

17.原式=2-6x-4-1-+-2V2-2=2>Z2*

2

A

Z.ABD=zCBAD=45°

AD=BD

\-ADxBC,BEJ.AC

•・.N.CAD+匕ACD=900

Z.CBE+zLACD=90°

・•.Z.CAD=ZLCBE

又・・•乙CDA=aBDF=90°

第19题冬田

AADC^ABDF•・.AC=BF

---AB=BC»BEJLAC.・.AE=EC即AC=2AEBF=2AE

(2)解：•・•△ADC^ABDFDF=CD=X<2"

2?

^RtACDF^p,CF=VDF+CD=2

BEXAC,AE=ECAF=FC=2

AD=AF+DF=2+>Z^

四、（每小题1。分，共20分）

20.（1）~

3

(3.")

（2）画树状（形）图的：(3.7I+6)

(JT.3)

(77.C+6)

(>/2+6.3>

(Jy+6.C)

列表得:

二次-

3S+6

3(3,v^-)(3,+6)

7r(.3)——

X/^+6(+6,3)(X<2+6,、/文)~~-----------------------------

由彳对状（形）图（或表格）可矢口，共有6种可能出现的结果，每种

结果出现的可能性相同，其中两次抽取的卡片上的实数之差为有

理数的结果有2种，分别为（V2,V2+6）和（V2+6,>Z2），因

此，两次抽取的卡片上的实数之差为有理数的概率为2=L.

63

21.解：（1）过点A作APJ.GF于P

由题意彳导AP=BF=12,AB=PF=1.4,

乙GAP=37°

CP

在RtZSPAG中.tanzlPAG=-^-

AP

GP=AP-tan370=12x0.75=9

GF=GP+PF=9+1.4=10.4

答风筝距地面的高度为10.4米.

（2）白题总可知MN=5,MF=3

在Rtz^MNF中，NF=V/MN^MF5=4

10.4-5-1.65=3.75<4能触到挂在W上的风筝

五、(本题1O分)

22.(1)证明：过点A作AF_LON于F

---OM是OA的切线

ABXOM

;OC平分心MOZ

AF=AB=2「.ON是。A的切线

(2)解一.•乙MON=60°,AB_LOM

zLOEB=30°

♦.AFXON,

ZLFAE=60°

在RtZXAEF中,tanZ.FAE=—

AF

EF=AF*tan600=2\/3

2

.-.Sc,=Sz,AEF-Sa^AO.=-l-AF.EF-^TTAF=2X<3-TT

六、（本题12分）

23.解（1））・=60『,OWxW管

（2）上午9点巾=80,戈2=6。

设需要开放a个普通售票奋口.

依题意得80K+60x5N1450Q14巨

8

•JX为整数.-.x=15

答：至少需要开放15个普通售票窗口

（3）解设力=k,x，把（1,80）代入得80=k,

>-,=80x当R=2时，八=160,上午1。点>2=羽=160

由（1）得当x=等时，,2=135

图之中一次函数过点（-,135）.（2,160）

2

设一次函数表达式为）-2=1（产+巳

3

—k-4-b=135k=50

122解得2

b=60

2k2+b=160

一次函数的表达式为1,?=50.、+60

七、(本题12分)

24.(1)证明•/四边形ABCD是矩形AD//BC

乙EAO=Z.BFO

又^AOE=zLFOB,AE=BF

AAOE^AFOBEO=BO

ZSAOE与ZiAOB是“友好三角形”

(2);aAOE与ADOE是“友好三角形”

A

^Z.AOE=^AOOE,AE=ED=AD=3

---AAOB与AAOE是“友好三角形”

…n^AOB-O/LAOE

△AOE^△FOB

8

,•,oS^AOE=sD乙FOB

第24邈答图

S乙AOO=SAA8F

**,Sjg边也COOF=S版用ABC。—2SAABF=4x6—2x—x4x3=12

探究：2或2X<3

/、、(本题14分)

---B(1,2>ZT)

当)=2时,2=§/、。8丝

55

解得：HI=1,A：2=4D(4,2y/2)

(3四边形OAEB是平行四边形

理由如下：抛物线的对称轴是工=亘

2

BE=^--1=AVA(A,0)OA=BE=—

222'2

X-.BE/7OA二四边形OAEB是平行四边形

②二'或WJ、

22

2013年北京市高级中等学校招生考试

数学试卷

满分120分，考试时间120分钟

一、选择题（本题共32分，每小题4分）

下面各题均有四个选项，其中只有二个是符合题意的。

1.在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提

出了总计约3960亿元的投资计•划。将3960用科学计数法表示应为

A.39.6X102B.3.96X103C.3.96X104D.3.96X104

3

2.一士的倒数是

4

4c.-2

A.-BTD.

3443

3.在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1,2,3,4,5,

从中随机摸出一个小球，其标号大于2的概率为

1234

-氏-C-

A.555D.5-

4.如图，直线。，力被直线c所截，a//hfZ1=Z2,若N3=40°,则N4等于

A.40°B.50°

C.70°D.80°，

5.如图，为估算某河的宽度，在河对岸边选定一个目标点A,在近岸

取点B,C,D,使得ABLBC,CD±BC,点E在BC上，并且点（第4题）

A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,

则河的宽度AB等于

A.60mB.40m

C.30mD.20m

6.下列图形中，是中心对称图形但不是轴对称图形的是（第5题WD

BCD.

7.某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示:

时间（小时）5678

人数1015205

则这50名学生这一周在校的平均体育锻炼时间是

A.6.2小时B.6.4小时C.6.5小时D.7小忖

8.如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=2,设

弦AP的长为x,aAPO的面积为y,则下列图象中，能表示y与

的函数关系的图象大致是（第8题）

二、填空题（本题共16分，每小题4分）

9.分解因式：ab2-4ab+4a=

10.请写出一个开口向上，并且与y轴交于点（0,1）的抛物线的解析式10

11.如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，

若AB=5,AD=12,则四边形ABOM的周长为

12.如图，在平面直角坐标系xO），中，已知直线/：f=—x—1,双

曲线y在/上取点A”过点A1作x轴的垂线交双曲线于

x

点B”过点Bi作y轴的垂线交/于点A2,请继续操作并探究：

过点A2作x轴的垂线交双曲线于点B2.过点B2作y轴的垂线

交/于点A3,…，这样依次得到/上的点Ai，A2,A3,…，An，…。

记点An的横坐标为明,若。1=2,贝1」。2=_________，«2013=_________；若要将上

述操作无限次地进行下去，则力不用牛的值是

三、解答题（本题共30分，每小题5分）

13.如图,已知D是AC上一点，AB=DA,DE〃AB,ZB=ZDAE（.

求证：BC=AE»

14.计算：(1-V3)0+|-V2|-2cos45°+

\3x>x-2

15.解不等式组：L+]

1-3->2x

16.已知--4x—1=0,求代数式（2%-3）2-（》+?）。一田一/2的值。

17.列方程或方程组解应用题：

某园林队计划由6名工人对180平方米的区域进行绿化，由于施工时增加了2名工

人，结果比计划提前3小时完成任务。若每人每小时绿化面积相同，求每人每小时的绿

化面积。

18.已知关于x的一元二次方程尤2+2x+2女—4=0有两个不相等的实数根

（1）求人的取值范围；

（2）若人为正整数，且该方程的根都是整数，求k的值。

四、解答题（本题共20分，每小题5分）

19.如图，在。ABCD中，F是AD的中点，延长BC到点E,

ffiCE=-BC,连结DE,CF,

2

（1）求证：四边形CEDF是平行四边形；

(2)若AB=4,AD=6,ZB=60°,求DE的长。

20.如图，AB是。。的直径，PA,PC分别与。。相切于点

A,C,PC交AB的延长线于点D,DELPO交PO的延

长线于点Eo

（1）求证：ZEPD=ZEDO

3

（2）若PC=6,tanZPDA=-,求OE的长。

4

（第20题）

21.第九届中国国际园林博览会（园博会）已于2013年5月18日在北京开幕，以下是根据

近几届园博会的相关数据绘制的统计图的•部分：

第六至第九届园博会第九届园博会

牡丹园面积为平方千米；

（2）第九届园博会园区陆地面积是植物花园区总面积的18倍，水面面积是第七、八两

届园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据；

（3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位

数量与日接待游客量和单日最多接待游客量中的某个量近似成正比例关系，根据小

娜的发现，请估计将于2015年举办的第十届园博会大约需要设置的停车位数量（直

接写出结果，精确到百位）。

第七届至第十届园博会游客量与停车位数量统计表

日均接待游客量单日最多接待游客量停车位数量

（万人次）（万人次）（个）

第七届0.86约3000

第八届2.38.2约4000

第九届8（预计）20（预计）约10500

第十届1.9（预计）7.4（预计）约

22.阅读下面材料：

小明遇到这样一个问题：如图1,在边长为a（a>2）的正方形ABCD各边上分别

截取AE=BF=CG=DH=1,当/AFQ=/BGM=/CHN=/DEP=45°时，求正方形MNPQ

的面积。

（第22题图1）

小明发现：分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,

S,T,W,可得△RQF,ASMG,ATNH,Z\WPE是四个全等的等腰直南三角形（如

图2)

请回答:

（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新

的正方形的边长为;

（2）求正方形MNPQ的面积。

参考小明思考问题的方法，解决问题：

如图3,在等边AABC各边上分别截取AD=BE=CF,

再分别过点D,E,F作BC,AC,AB的垂线，得到等边

（第22题图3）

△RPQ,若S改0°=内-,则AD的长为。

五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）

23.在平面直角坐标系xOy中，抛物线VA

y=mx2-2mx-2（mw0）与y轴交于点A,

其对称轴与x轴交于点B。

（1）求点A,B的坐标；

（2）设直线/与直线AB关于该抛物线的对称轴对

O

称，求直线/的解析式；

（3）若该抛物线在—2<x<—1这一段位于直线I

的上方，并且在2<x<3这一段位于直线

AB的下方，求该抛物线的解析式。

（第23题）

24.在aABC中，AB=AC,ZBAC=a（0°<a<60°）,将线段BC绕点B逆时针旋转

60°得到线段BD。

（1）如图1,直接写出/ABD的大小（用含a的式子表示）；

（2）如图2,ZBCE=150°,ZABE=60°,判断4ABE的形状并加以证明;

（3）在（2）的条件下，连结DE,若NDEC=45°,求二的值。

25.对于平面直角坐标系xOy中的点P和。C,给出如下定义：若。C上存在两个点A,B,

使得NAPB=60°,则称P为。C的关联点。

已知点D（工，-）,E（0,-2）,F（2石，0）

22

（1）当。O的半径为1时，

①在点D,E,F中，。。的关联点是；

②过点F作直线/交y轴正半轴于点G,使NGFO=30°,若直线/上的点P（〃？，

n）是。O的关联点，求〃?的取值范围；

（2）若线段EF上的所有点都是某个圆的关联点，求这个圆的半径，的取值范围。

斗

O?

（第25题）

2013北京中考数学试题答案

选并虺（共32分，何虺4分）

l-XBIX（BABA

.珀:虺（H16分,作超4分）

»“（/，2）'】0.吾泉不用I）11.20\2,｛。和I

vtn»（具却分.每㈱$分）

13.ill：内为’（4S：4）,用以“〃：（余线的形"同边加③）

L币

I4.M：双式If7z2*生，45

2

I，就：不第，WI的第张为l<r<l

S

lh|¥:原式l2r+9.

"4*Ifl-hKt.it12

I7.M：设句人体小时的绿化面积为*f力*

I…,1X01X0,

依题4————+]

hxKr

解存Ky

"检的』原力和的解

答：何人能小时的纭化向枳1-i-Ih米

2

IXm；<I）A>（hAe-

2

（2）k2

四、irnjft（共TO分，件鹿s分）

I9.ii!:(I)WillCE//FD.CiF〃1：H四边形CEDI：此fhFI边形

%(2)DEVi5

20if：(I)WZfi/X?-AIK)./Alt)Z(P(fiH/EPI)/EDO

Wi：(2)CE-F

21.M；(1)003(2)笫/MN(他面积3.6Thr米,水血血枳1.5Ih\t

(3)3,7x10,

22帆(I)«t(2)2::

h.解答J»(共22分,23师7分.24虺7分,2X]»X分)

23.W：(I)Ut.M(0,-2),0(1,0)：

(2)设在戊/杆机式为ykth.

根据而称.财木"1战/5、线4HXI，相对称，二|'|线/过(0.2).

乂；如⑼，

•,」?:ZH/•二八找/第机式为y-2JM2,

[4>A-0|fr-2

(3)«UK时除."物线42<"-1这段付于H线，的Ih.和二IM物Mi府3VJTV4这

一段位卜汽线48的Ih.

乂・"t2<，<3这偿位I九线柿的卜力.

，微物”过点(3.4)....IM物线M机式为y2/4«2.

24.(I)/ABD-30"--；

2

(2)等功三例形；

连接力〃、(7J."JNA8C”为等边的形.

/IAABI)和AACf»'I1.

AH=AC

*：、AD-Aii

Hb-CD

.'A砌(SSS)

.'./AIWI5(r.

/hAABD和A£H(,中.

ZEHC

'：HI)«('

/BbA/KA

，A〃"，匕△£7«/(ASA)

:.HAHE.乂V/AHE«r.:./\ABE为牛边形.

（3）由（2）柑./IK/•；9（尸.Z'."//«•：（'45".，△仅/为等胺1*（角加形.

：.CDCh：CH.：.DAl）H,/DAHI5U.：.aKr.

25.航：（I）⑴〃,b：

⑵00,”/.白线。网和团,I'L”外的点如果作冽的切线.此时切点I点〃以及阴心织底

的小30。,谟小叫佗是大联点,相切如果正好是健.则应味看点到M心的小博等I2.

”八（g*2）4,m.点到IW心的即出小I2的均"J以是及以也

（2）r21.压他的中点存M心.此时惘的最小T衿为I

2013年湖北省12市，区中考数学试题

荆州市2013年初中升学考试数学试题

一.选择题：

1.下列等式成立的是A

A.\-2|=2(V2-1)0=0C.(--)~'=2

2

2.如图，AB//CD,NABE=60°,ZZ>=50°,则/E的度数为C

4.30°8.20°C.1O00.40°

3•解分式方程-X------2---=1时，去分母后可得到C

3+x2+x

4冗(2+尤)—2(3+x尸1x(2+x)—2=2+x.com第2题图

C.x(2+x)—2(3+x)=(2+x)(3+/)DJC—2(3+X)=3+X

4.计算*+3卜瓜的结果是B

A,V3+5/2B.V3c由D.V3—V2

3

5.四川雅安发生地震灾害后，某中学九（1）班学生积极捐款献爱心，如图所示是该班50名

学生的捐款情况统计，则他们捐款金额的众数和中位数分别是B

A.20,108.10,20C.16,150.15,16

第5题图第6题第8题

6.如图，在△4BC中，BOAC,点。在8c上，且。C=4C,角乙4c8的平分线CE交A。

于E,点尸是AB的中点，则S》EF：S叫.BDEF为D

A.3：4BA-.2C,2：3DA：3

7.体育课上，20人一组进行足球比赛，每人射点球5次，已知某一组的进球总数为49个，

进球情况记录如下表，其中进2个球的有x人，进3个球的有y人，若（x,y）恰好是两条

直线的交点坐标，则这两条直线的解析式是D

进球数012345

人数15Xy32

A.y=x+9与尸8.广―x+9与

C.y=-x+9与y=-Q.y=r+9与y=-§x+彳

8.如图，将含60°角的直角三角板ABC绕顶点4顺时针旋转45°度后得到△48'C,，点8

经过的路径为弧B8',若角/84C=60°,AC=1,则图中阴影部分的面积是A

9.将一边长为2的正方形纸片折成四部分，再沿折痕折起来，恰好能不重叠地搭建成一个三

棱锥，则三棱锥四个面中最小的面积是C

10.如图，在平面直角坐标系中，直.线y=-3x+3与x轴、y轴分别交

于A、8两点，以AB为边在第一象限作正方形48C。沿x轴负方向

平移a个单位长度后，点C恰好落在双曲线上则«的值是B

AAB.2C.30.4

二.填空题：

11.分解因式a3一而2=

12.如图，在高度是21米的小山4处没得建筑物CC顶部C处的仰角为30°,底部。处的

俯角为何45°,

则这个建筑物的高度CO=_7ji+21米（结果可保留根号）

第12题图第13题图第14题图

13.如图，是一个4X4的正方形网格，每个小正方形的边长为1.请你在网格中以左上角的三

角形为基本图形，通过平移、对称或旋转变换，设计一个精美图案，使其满足：①既是轴对

称图形，又是以点O为对称中心的中心对称图形；②所作图案用阴影标识，且阴影部分面

积为4.

14如图，△A8C是斜边48的长为3的等腰直角三角形，在△4BC内作第1个内接正方形

AIBNIEI（囱、鼠在43上，e分别在AC、BC上），再在△48C内接同样的方法作

第2个内接正方形4为外瓦，…如此下去，操作"次，则第"个小正方形A点,Q.E”的边长

2k-1

15.若根式有意义,则双曲线y=-----与抛物线y=x2+2x+2-2k的交点在第2

V2—2kx

象限.

16.在实数范围内规定新运算“△”，其规则是：必424一瓦已知不等式无的解集在

数轴上如图表示，则k的值是-3

第16题图

17.如图，△4CE是以a4BC£>的对角线AC为边的等边三角形，点C与点E关于x轴对称.

若E点的坐标是（7,一3百），则。点的坐标是,

18.如图，将矩形A8C。沿对角线AC剪开，再把△AC。沿C4方向平移得到△A1C1O1,连

结ADI、BC1.若NAC8=30°,AB=\,CC\=x,八4仪）与△A1C1O1重叠部分的面积为s,

则下列结论：①△AlAOlg/SCClB；②当x=l时，四边形4BC1O1是菱形；③当k2时，

/\BDD\为等边三角形；④$=且。一2尸（0<x<2）；其中正确的是

8

（填序号）.

三“解答题：

19.用代入消元法解方程组

第20题图

x-y-2...①

3x+5y=14…②

20.如图，ZXABC与△（:£>£>均是等腰直角三角形，ZACB=ZDCE=90°,。在A8上，连

结8E.请找出一对全等三角形，并说明理由.

21.我市某中学为备战省运会，在校运动队的学生中进行了全能选手的选拔，并将参加选拔

学生的综合成绩（得分为整数，满分为100分）分成四组，绘成了如下尚不完整的统计图表.

组别成绩组中值频数

第一组90<x<100954

第二组80Wx<9085m

第三组70<x<8075n

第四组60«706521

根据图表信息，回答下列问题：

（1）参加活动选拔的学生共有人；表中,n=；

（2）若将各组的组中值视为该组的平均值，请你估算参加选拔学生的平均成绩；

（3）将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,

现决定随机挑选其中两名学生代表学校参赛，试通过画树形图或列表的方法求恰好选中A

和8的概率.

22.已知：关于x的方程kx2—（3k-l）x+2（k—1）=0

（1）求证：无论k为何实数，方程总有实数根；

（2）若此方程有两个实数根卬处,且Ix,-x2|=2,求k的值.

23.如图，48为。。的直径，弦CO与A8相交于E,DE=EC,过点8的切线与4。的延长

线交于尸，过E作EGJ_BC于G,延长GE交于”.

4

（1）求证：AH=HD；（2）若cos/C=—，DF=9,求。。的半径.

5

第24题图

24.某个体户购进一批时令水果，20天销售完毕.他将本次销借情况进行了跟踪记录，根据所

记录的数据可绘制如图所示的函数图象，其中II销售量y（千克）与销售时间x（天）之间

的函数关系如图甲所示，销售单价0（元/千克）与销售时间x（天）之间的函数关系如图乙

所示.

（1）直接写出y与x之间的函数关系式；

（2）分别求出第10天和第15天的销售金额；

（3）若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中“最佳销

售期”共有多少天？在此期间销售单价最高为多少元？

25.已知：如图①，直线产一百户百与x轴、y轴分别交于A、B两点，两动点。、E

分别从A