立体几何基础题题库-

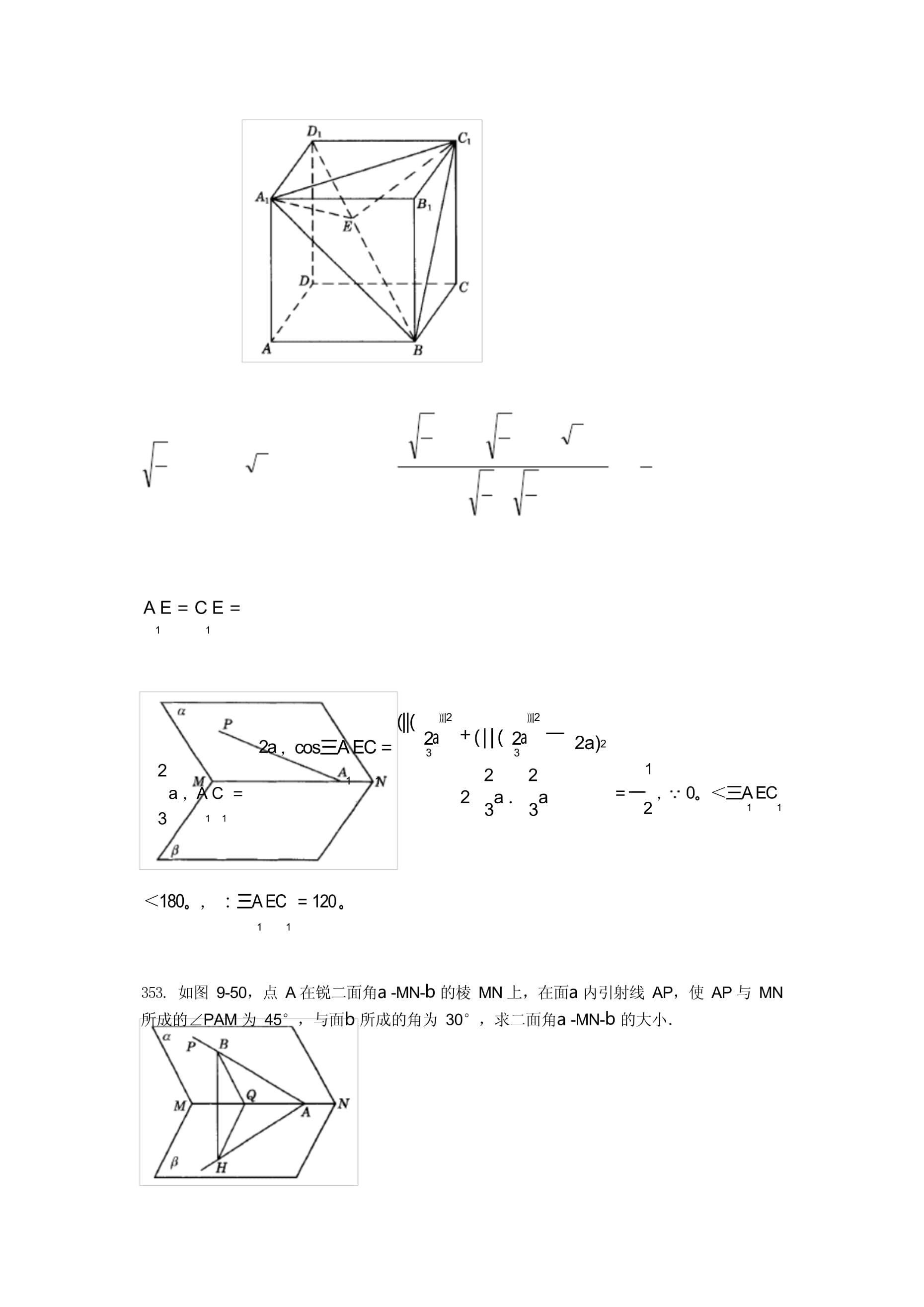
立体几何基础题题库351-400(有详细答案)ay1111111111111111111111111211121113a311231122111112中∠BHA=90°，∠BAH=30°，∴BH=a．在Rt△BHQ中，∠BHQ=90°，BQ=a，2BH=2a，sin三BQH=BH=2a2=2，∵∠BQH是锐角，∴∠BQH=452BQa2即二面角a-MN-等于45°．其中正确的两个命题是()力.不一定平行，故(2)不正确.故应排除A、C.依题意，有两个命题正确，不可能(3)，(4)都正mm)是不正确的，因此可或(3)检查，只须检查一个便可以做出判断.为棱，将正方形的纸折成直二面角，则∠BOD等于()A.120°B.150°C.135°D.90°垂直，余弦定理，以及空间与平面问题的转化能力。22如图，设正方形边长为a，由O为正方形中心，则BO＝a,DO＝a，连AB，因为DA22a2a26AD2+AE2+BE2＝a2++=a.442226a2+a2a2444＝＝＝a2找出空间转化为平面的途径，几何计算的准确性等。B30°，则线段CD的长为取值范围是()A.[1，+∞]233234333233以及空间想象能力和几何计算.2323∩α＝l，在y内，DC⊥l时为最短，此时DC＝DA′·tan30°＝.故CD≥.∴应331357.如图，四棱锥P—ABCD的底面是直角梯形，AB∥DC，AB⊥BC，且AB＝CD，侧棱PB2共棱.有了公共棱，二面角的平面角就生了根.ABDCABBCDCBCPB面ABCD.1∵AB＝CD，PC＝5，BC＝3，∴PB＝4.2S＝6，∴AB＝3，CD＝6，ΔPABEABEB1＝＝.DCEC2.5DC65在直角ΔDCF中，tanα＝＝＝.CF24455α＝antan.4评析：这是一道较难的题，难就难在怎么确定两相交平面的交线.由公理二交线的唯一性必∴在ΔDEF中，cos∠EDF＝22-3,又-1＜22-3＜0.∴二面角A—SC—B的平面角∠EDF＝arccos(22-3)＝π-arccos(3-22)同时取特殊值可以使问题简单化.最大值.2SAEDCEAEADCAEDCS，AE＝.2ABCaEBAE4S∴∠ABE＝30°，在ΔAEB中，有＝，∴EB＝sin(α+30°).4S14S据题意，有α∈(0°，180°)，当α＝60°时，有EB＝，这时(S)＝a·＝maxaΔDBCmax2a2S.这一章的一些主要知识.C就行了.1sin9∴tanα＝sinθ,cosα＝,sinα＝+sin291+sin29. a＝PQsinsina,asinaasin9∴PQ＝＝.解法略为简便些.11写出一个可能的值)查锥体求积公式这个知识点，的.排除{1，1，2}，可得{1，1，1}，{1，2，2}，{2，2，2}，然后由这三类面在空间构造满足条件的一个四面体，再求其体积.少可构造出二类满足条件的四面体，五条边为2，另一边为1，对棱相等的四面体.BCM把三棱锥分成两个三棱锥，由对称性可知AD⊥面BCM，且V=V，所以A—BCMD—BCM1V=S·AD.ABCD3ΔBCMMN=MN=CM2CN2=1==，，从而S==，222ΔBCM22故V=××1=.ABCD326对于对棱相等的四面体，可参见图2.其体积的计算可先将其置于一个长方体之中，再用长方体的体积减去四个小三棱锥的体积来进行.亦可套公式2V=·(a2+b2c2)(b2+c2a2)(c2+a2b2)，214=·7=.1212363.湖结冰时，一个球漂在其上，取出后(未弄破冰)，冰面上留下了一个直径为24cm,深364.在有阳光时，一根长为3米的旗轩垂直于水平地面，它的影长为3米，同时将一个半径为3米的球放在这块水平地面上，如图所示，求球的阴影部分的面积(结果用无理数表示).能够放入这个棱锥的最大球的半径.BDBD」ACJ1由此，面MAD⊥面AC.ΔAMD∴ME＝.MF＝aar＝ra2a22当且仅当a＝，即a＝2时，等号成立.a∴当AD＝ME＝2时，满足条件的球最大半径为2-1.1111(1)1.11.1.11.(2)AB=BC=BB亭G为△ABC的中心.AC=2a112262332336∴BG=a6∴BG=a2_(a)2=36a2_a2=9a2=a931难难相∴cos∠BBG=1BB6a6a3367.已知P为ABCD所在平面外一点，M为PB的中点，求证：PD∥平面MAC．证明连AC交BD于O，连MO，则MO为△PBD的中位线，∴PD∥MO，∵PD亿平面MAC，MO平面MAC，∴PD∥平面MAC．11111368.如图，在正方体ABCD－ABCD中，M，N111111111，AD，11111(1)求证：AE⊥平面ABMN．11(2)平面直线AE与MF所成的角．1111111平面中的问题，只要画出平面几何图形，用平几知识解决．(2)为(1)的应用．1证明(1)∵AB⊥平面A11111∴AB⊥AE．在平面AADD中，111111解(2)由(1)知A1E⊥平面ABMN，而MF仁平面ABMN，∴1AE⊥MF，11则AE与MF所成的角为90°111111369.如图，在正方体ABCD－ABCD中，M为棱CC的中点，AC111111111111方法1：发现AO平分DB，想到什么？(△ADB是否为等腰三角形)111111111111111tan∠MOC=2，∴∠AAO=∠MOC，则∠AOA＋∠MOC＝90°，∴AO⊥OM，∵OM∩21111OMBD1333(2)A，B在平面α的异侧时，P平面α的距离为333种情形的结论，就是将(1)结论中的b改为(－b)，而无需再画另一图形加以求解．(A)有且只有一个(B)可能存在也可能不存在(C)有无数多个(D)一定不存在(B)11111372.在正方体ABCD－ABCD中，若11111直线CE垂直于)111(A)AC(B)BD(C)AD(D111：(B)111BD⊥AC，BD⊥CC，∴BD⊥平面AACC111P不在△ABC所在平面内，过P作平面α，使△ABC的三个顶点到α的距离相等，这样的平面共有)(A)1个(B)2个(C)3个(D)4个(A)1(B)2(C)3(D)4h1：2，则P到平面α的距离为．33异侧时，P到平面α的距离为6291＝1(cm)．33且它们在α的同一侧，则△ABC的重心到平面α的距离为．3ED＝．AB＝10，∴CD＝5，则ED＝52+122＝13．378.如图，在正方体ABCD－ABCD中，求：11111111．D1111111111111111111111111111111即H为B在平面ACB内的射影．另在求此角大小时，只要求∠BBO即可．11111111111111111111111111111111111sin∠BAO＝BO=1，∴∠BAO＝30°．1AB211111111111111111111111111111111BB211121379.Rt△ABC中，∠C＝90°，BC＝36，若平面ABC外一点P与平面A，B，C三点等距(1)求证：PM⊥AC；(2)求P到直线AC的距离；(3)求PM与平面ABC所成角的正切值．角三角形，其外心为斜边的中点．证明(1)∵PA＝PC，M是AC中点，∴PM⊥AC解(2)∵BC＝36，∴MH＝18，又PH＝80，(3)∵PM=PB=PC，∴P在平面ABC内的射线为△ABC的外心，PH040PH040MH932336又∵CM＝3a，∴CN＝CM2MN2=7a=21a．126CM3111111解析：在空间中作出两条直线垂直相对较在平面内作两条直线垂直难．此题CM与MN是相1交直线，一种方法可通过勾股定理来验证它是否垂直，另一方法为：因MN是平面AABB内1111证明1设正方体的棱长为a，则MN＝5a，4122144MN111证明2连结BM，∵CB⊥平面AABB，1111111114221121111PA＝a．(1)求证：PC⊥CD；(2)求点B到直线PC的距离．解析：(1)要证PC与CD垂直，只要证明AC与CD垂直，可按实际情形画出底面图形进行实上，这里的∠PBC＝90°)；另一种重要的思想是：因PC在平面PAC中，而所作BH为平证明(1)取AD的中点E，连AC，CE，a623383.四面体ABCD的四个面中，是直角三角形的面至多有()(A)1个(B)2个(C)3个(D)4个111(A)锐角三角形(B)直角三角形(C)钝角三角形(D)以上都不对AB1111离等于∵PA＝PB＝PC,∴P在平面α内的射影为△ABC的外心O，∵∠C＝90°，∴O为AB的中点，∵AO＝5，PA＝7，∴PO＝7252=26(1)求证：MN⊥CD；(2)若∠PDA＝45°，求证：MN⊥平面PCD．证明(1)连AC∩BD＝O，连NO，MO，则NO∥PA．∵PA⊥平面ABCD，∴NO⊥平面ABCD．(2)∵∠PDA＝45°，∴PA＝AD，P：：PA⊥CDBDDA113注要充分注意平面几何中的知识(如本题中三角形重心性质，等腰三角形性质等)在证题EEEF仁平面AEF∴a⊥EFAaPHCHCAB角三PHACB2cos∠DBP=∴∠DBP=45°,即PB与平面BCD所成角为45°．22∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中，BE=a,BP=2a,∴∠BPE=30°即2BCEDCDPP393.正四棱锥的一个对角面与一个侧面的面积之比为6:2，求侧面与底面所成的角的大PCAB解析：如图，正四棱锥P—ABCD的一个对角面△PAC。设棱锥的底面边长为a，高为h，斜11PACPAC2PBC2COAEB21∴S:S=ah:ah,=2h:h,=6:2PACPBC22POh3在Rt△POE中，sin∠PEO===，PEh,2几几∴∠PEO=，即侧面与底面所成的角为.3(1)求证：AC⊥面ABC1；(2)求证：C1点在平面ABC上的射影H在直线AB上；(3)求此三棱柱体积的最小值。析：(1)由棱柱性质，可知A1C1//AC(3)连结HC，由(2)知C1H」平面ABC，11V=S.CH=ABACCH=323CH=33CH棱柱ABC1212C1111111111111111111111111111由三垂线定理，下证AC⊥AM即可1111113，AA=CC=6116MC∵1=CAMC∴1=CA3ACAA122ACAA16221111又∠2+∠3=90011评注：利用三垂线定理的关键是找到基本面后找平面的垂线111121 (1)求△ADE的面积；(2)求证：平面ADE⊥平面ACCA。11解析：分别在三个侧面内求出△ADE的边长AE=2a，AD=5a，DE=BC2+(ECBD)2=a2+(a)2=5a222225262a(a)2(a)2=a224(2)∵底面ABC⊥侧面AACC1∴△ABC边AC上的高BM⊥侧面AACC1122∴DN⊥平面AACC11∴平面ADE⊥平面AACC11397.斜三棱柱ABC—ABC中，底面是边长为4cm的正三角形，侧棱AA与底面两边AB、AC11111 1111111AA面BBCC的距离。1111AAB∠AAC111ABC1 3S=S=AB.AAsin三AAB=47=143AA1C1CAA1B1B11211111BBCC11SSA1B1C1ABC4全全 (3)∵cos∠AAB=cos∠AAO·cos∠OAB1cosAAO