最小二乘类辨识算法

最小二乘类辨识算法第一页，共一百四十三页，2022年，8月28日2

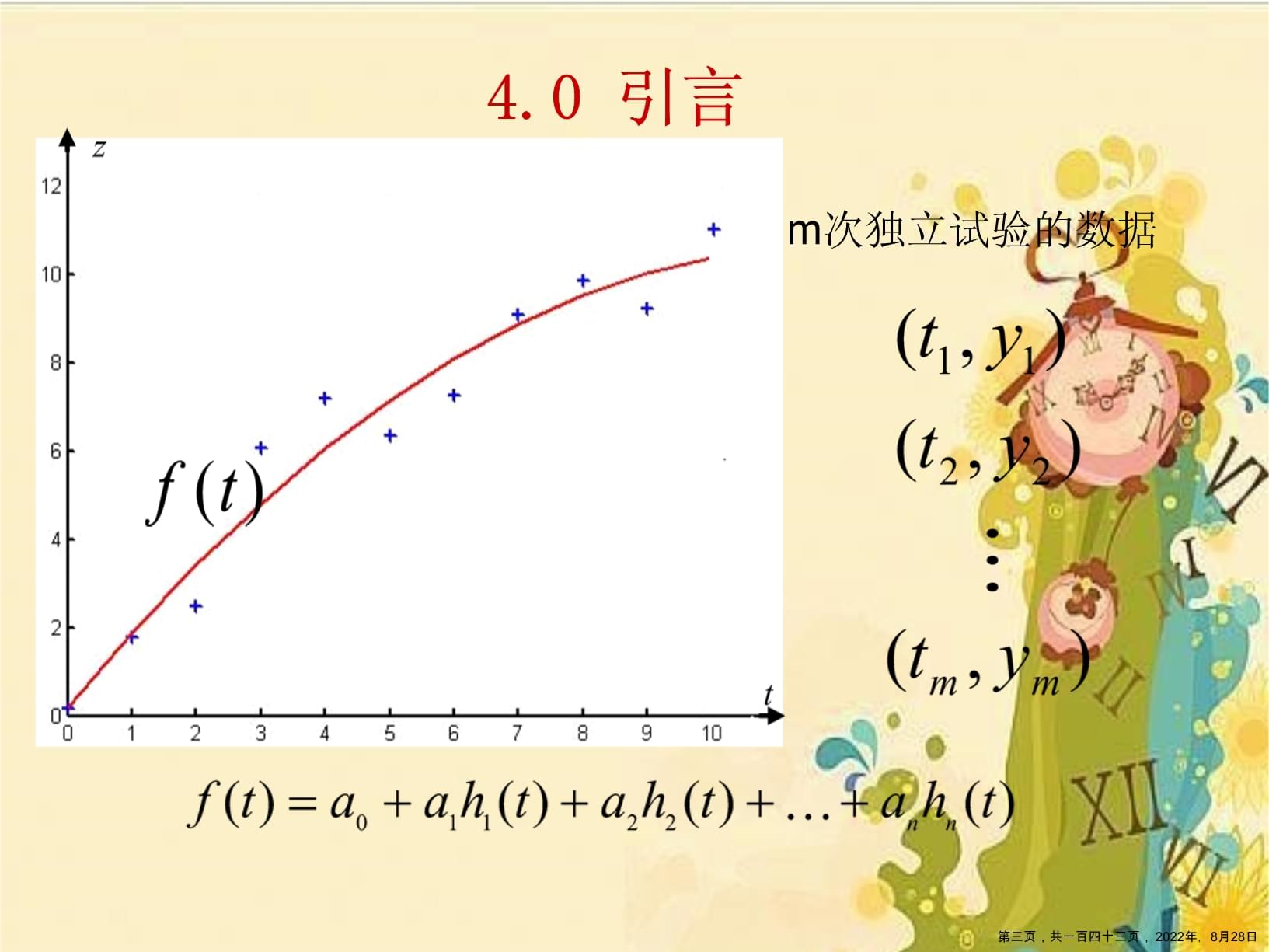
4.0引言4.1最小二乘法的基本概念4.2最小二乘问题的提法4.3最小二乘问题的解4.4最小二乘估计的可辨识性4.5最小二乘估计的几何解析4.6最小二乘参数估计值的统计性质4.7噪声方差估计4.8最小二乘参数估计的递推算法第二页，共一百四十三页，2022年，8月28日m次独立试验的数据4.0引言第三页，共一百四十三页，2022年，8月28日

1801年初，天文学家皮亚齐发现了谷神星。1801年末，天文爱好者奥博斯，在高斯预言的时间里，再次发现谷神星。1802年又成功地预测了智神星的轨道。高斯自己独创了一套行星轨道计算理论。高斯仅用1小时就算出了谷神星的轨道形状，并进行了预测1794年，高斯提出了最小二乘的思想。第四页，共一百四十三页，2022年，8月28日1794年，高斯提出的最小二乘的基本原理是

未知量的最可能值是使各项实际观测值和计算值之间差的平方乘以其精确度的数值以后的和为最小。第五页，共一百四十三页，2022年，8月28日6最小二乘类辨识算法的主要内容最小二乘辨识算法自适应辨识算法偏差补偿最小二乘法增广最小二乘算法广义最小二乘法辅助变量法相关二步法第六页，共一百四十三页，2022年，8月28日7如果仅仅关心所要辨识的过程输入输出特性可以将所过程视为“黑箱”而不考虑过程的内部机理第七页，共一百四十三页，2022年，8月28日8过程的“黑箱”结构u(k)和z(k)分别是过程的输入和输出

-描述输入输出关系的模型，称为过程模型第八页，共一百四十三页，2022年，8月28日9

通常可以表示成其中

（）（）第九页，共一百四十三页，2022年，8月28日10{n(k)}为噪声可以表示成均值为零的平稳随机系列

式中

（）（）（）第十页，共一百四十三页，2022年，8月28日11各种方法所用的辨识模型结构略有不同最小二乘法（受控自回归CAR模型）增广最小二乘法(受控自回归滑动平均CARMA模型)广义最小二乘法(动态调节DA模型)（）（）（）第十一页，共一百四十三页，2022年，8月28日12经比较可以看出各种方法所用过程模型一样只是噪声模型有所不同

第十二页，共一百四十三页，2022年，8月28日根据不同的辨识原理，参数模型辨识方法可归纳成三类：①最小二乘类参数辨识方法，其基本思想是通过极小化如下准则函数来估计模型参数：其中

代表模型输出与系统输出的偏差。典型的方法有最小二乘法、增广最小二乘法、辅助变量法、广义最小二乘法等。（）第十三页，共一百四十三页，2022年，8月28日②梯度校正参数辨识方法，其基本思想是沿着准则函数负梯度方向逐步修正模型参数，使准则函数达到最小，如随机逼近法。③概率密度逼近参数辨识方法，其基本思想是使输出z的条件概率密度

最大限度地逼近条件

下的概率密度

，即

典型的方法是极大似然法。（）第十四页，共一百四十三页，2022年，8月28日15

4.1最小二乘法的基本概念最小二乘法

1795年高斯在其著名的星体运动轨迹预报研究工作中提出的,后来成了估计理论的奠基石。最小二乘的基本结果有两种算法：①一次完成算法或批处理算法：利用一批观测数据，一次计算或经反复迭代，以获得模型参数的估计值。第十五页，共一百四十三页，2022年，8月28日②递推算法：在上次模型参数估计值

的基础上，根据当前获得的数据提出修正，进而获得本次模型参数估计值

，广泛采用的递推算法形式为其中

表示k时刻的模型参数估计值，K(k)为算法的增益，h(k-d)是由观测数据组成的输入数据向量，d

为整数，

表示新息。（）第十六页，共一百四十三页，2022年，8月28日17假设过程的输入输出关系可以描述成以下最小二乘格式z(k)―过程的输出

―参数h(k)―观测的数据向量n(k)―均值为零的随机噪声（）第十七页，共一百四十三页，2022年，8月28日18利用数据序列{z(k)}和{h(k)}极小化下列准则函数使J最小的的估计值，称为的最小二乘估计值。

（）第十八页，共一百四十三页，2022年，8月28日●最小二乘原理表明，未知参数估计问题，就是求参数估计值

，使序列的估计值尽可能地接近实际序列，两者的接近程度用实际序列与序列估计值之差的平方和来度量。●最小二乘估计值应在观测值与估计值之累次误差的平方和达到最小值处，所得到的模型输出能最好地逼近实际系统的输出。第十九页，共一百四十三页，2022年，8月28日20４.2

最小二乘问题的提法

设时不变SISO动态过程的数学模型为所要解决的最小二乘问题如何利用过程的输入、输出数据确定多项式和的系数

（）第二十页，共一百四十三页，2022年，8月28日21在最小二乘问题中，一般对模型作以下假设首先，模型的阶次，已定且一般其次，将（）模型写成最小二乘格式式中

（）（）第二十一页，共一百四十三页，2022年，8月28日22对(4.1.5)式构成一个线性方程组可以写成

（）第二十二页，共一百四十三页，2022年，8月28日23

（）第二十三页，共一百四十三页，2022年，8月28日24另外设模型的噪声n(k)特征为

（）第二十四页，共一百四十三页，2022年，8月28日25在最小二乘法中假定{n(k)}是白噪声序列

-n(k)的方差最后，假设数据长度

（）（）第二十五页，共一百四十三页，2022年，8月28日(4.2.4)式有L个方程，包括个未知数。如果，方程的个数少于未知数的个数，模型参数不是唯一确定。如果，则只有当时，才有唯一确定解。当时，只有取，才有可能确定一个最优的模型参数，而且为了保证辨识的精度，L必须充分大。第二十六页，共一百四十三页，2022年，8月28日27４.3

最小二乘问题的解

取准则函数

-加权因子，对如K=1时，K=L时

体现对不同时刻的数据给予不同程度的信任（）第二十七页，共一百四十三页，2022年，8月28日28准则函数可写成二次型形式

-加权矩，一般为正定的对角矩阵

（）（）第二十八页，共一百四十三页，2022年，8月28日29设使则有则得

（）（）（）第二十九页，共一百四十三页，2022年，8月28日30当可逆时（称为正则）时充分条件因所以,是唯一的

（）（）第三十页，共一百四十三页，2022年，8月28日31通过极小化（）式计算称为加权最小二乘法取则（）式变化成

-最小二乘估计值

（）（）第三十一页，共一百四十三页，2022年，8月28日32上述最小二乘法的计算步骤为：首先获取一批足够数量的过程输入输出数据和，并确定加权矩阵，计算的逆矩阵（要求必须是正则矩阵），按照式(4.3.7)即可计算出过程参数的估计值。这种方法称为“一次完成算法”，它为理论分析提供了便利，但在计算时需要对矩阵求逆，如果矩阵维数过大，矩阵求逆的计算量将急剧增加，对计算机造成一定的负担。较为实用的方法是“递推算法”，即把式(4.3.7)化成递推计算的形式，这样便于实现在线辨识。第三十二页，共一百四十三页，2022年，8月28日33一次性完成算法要求必须是正则矩阵，其充分必要条件是过程的输入信号必须是２ｎ阶持续激励信号。即要求

（）第三十三页，共一百四十三页，2022年，8月28日34其中（）第三十四页，共一百四十三页，2022年，8月28日35上述条件称为开环可辨识性条件。即辨识所用的输入信号不能随意选择，否则可能造成不可辨识。目前常用的信号有：１）随机序列（白噪声）２）伪随机序列（如Ｍ序列）３）离散序列，通常指对含有ｎ种频率（各频率不能满足整数倍关系）的正弦信号进行采样处理获得的离散序列。第三十五页，共一百四十三页，2022年，8月28日例

考虑仿真对象选择如下的辨识模型进行一般的最小二乘参数辨识。

式中，v(k)是服从正态分布的白噪声N(0,1)。输入信号采用4阶M序列，其幅值为1.第三十六页，共一百四十三页，2022年，8月28日4阶M序列输出信号第三十七页，共一百四十三页，2022年，8月28日第三十八页，共一百四十三页，2022年，8月28日第三十九页，共一百四十三页，2022年，8月28日一般最小二乘参数辨识流程图第四十页，共一百四十三页，2022年，8月28日第四十一页，共一百四十三页，2022年，8月28日第四十二页，共一百四十三页，2022年，8月28日第四十三页，共一百四十三页，2022年，8月28日第四十四页，共一百四十三页，2022年，8月28日第四十五页，共一百四十三页，2022年，8月28日第四十六页，共一百四十三页，2022年，8月28日第四十七页，共一百四十三页，2022年，8月28日第四十八页，共一百四十三页，2022年，8月28日第四十九页，共一百四十三页，2022年，8月28日第五十页，共一百四十三页，2022年，8月28日第五十一页，共一百四十三页，2022年，8月28日第五十二页，共一百四十三页，2022年，8月28日第五十三页，共一百四十三页，2022年，8月28日第五十四页，共一百四十三页，2022年，8月28日第五十五页，共一百四十三页，2022年，8月28日56４.6最小二乘参数估计值的统计性质

最小二乘参数估计值具有随机性，因此需要研究它们的统计性质1.无偏性2.参数估计偏差的协方差性质3．一致性4.有效性5.渐近正态性第五十六页，共一百四十三页，2022年，8月28日571.无偏性(无偏性是用来衡量参数估计值是否围绕真值波动的一个性质。)定理1

若模型中的噪声向量的均值为零，即，并且与是统计独立的，即，则加权最小二乘参数估计值是无偏估计量，即其中表示系统的真实值。(4.6.1)第五十七页，共一百四十三页，2022年，8月28日58证明:根据（）及定理1所给的条件，参数估计量的数学期望为所以是无偏估计。(4.6.2)第五十八页，共一百四十三页，2022年，8月28日59无偏性并不要求噪声一定是白噪声，只要求它与统计独立即可。如果是白噪声，则与一定统计独立。另外，定理１所给出是条件是为无偏估计的充分条件，并不是必要条件。它的必要条件应是(4.6.3)第五十九页，共一百四十三页，2022年，8月28日60即与正交。当定理１的条件不能满足时，它提供了一种获取无偏估计的方法，即可通过选择加权矩阵使之满足正交条件。第六十页，共一百四十三页，2022年，8月28日612.参数估计偏差的协方差性质

（

参数估计偏差的协方差阵是用来评价参数估计精度的一个依据。）定理2

若模型的是均值为零，即，协方差阵为，并且与

统计独立的噪声向量，则参数估计偏差

的协方差阵为(4.6.4)第六十一页，共一百四十三页，2022年，8月28日62

证明：根据（）及定理1、定理2所给出的条件，有(4.6.5)第六十二页，共一百四十三页，2022年，8月28日63推论1，在定理2的条件下，如果加权矩阵

，则模型的参数估计值为相应的参数估计偏差的协方差为

此时参数的估计值称为Markov估计，或最小方差估计(4.6.7)(4.6.6)第六十三页，共一百四十三页，2022年，8月28日64推论2若模型中的是零均值的白噪声向量，且加权矩阵取，则参数估计偏差的协方差阵为

其中

是噪声的方差，且定义（）

第六十四页，共一百四十三页，2022年，8月28日

推论1、推论2可以由定理2直接得出，它们是评价最小二乘参数辨识方法的重要依据。如果噪声同时又服从正态分布，则（）式给出的参数估计值其偏差的方差达到最小值，称为最小方差估计，也称Markov估计。65第六十五页，共一百四十三页，2022年，8月28日663．一致性如果估计值具有一致性，说明它将以概率1收敛于真值。定理3在推论2的条件下，最小二乘参数估计是一致性收敛的，即w.p（withprobability）1W.P.1(4.6.9)第六十六页，共一百四十三页，2022年，8月28日67证明：根据（）式，有式中将依概率1收敛于一个正定阵，且是有界的，因而（）（）第六十七页，共一百四十三页，2022年，8月28日68又因所以（）第六十八页，共一百四十三页，2022年，8月28日69需要特别指出：只有当是白噪声时，定理３才能成立。第六十九页，共一百四十三页，2022年，8月28日第七十页，共一百四十三页，2022年，8月28日第七十一页，共一百四十三页，2022年，8月28日第七十二页，共一百四十三页，2022年，8月28日第七十三页，共一百四十三页，2022年，8月28日744.有效性即估计值偏差的协方差阵将达到最小值。定理4

在推论2的条件下，并设噪声服从正态分布，则最小二乘参数估计是有效估计值，即参数估计偏差的协方差达到Cramer-Rao不等式的下界其中，M为Fisher信息矩阵

（）（）第七十四页，共一百四十三页，2022年，8月28日75证明：因为其中由定理3知（）（）第七十五页，共一百四十三页，2022年，8月28日76则，故有那么即（）（）（）第七十六页，共一百四十三页，2022年，8月28日77上式取偏导数，得于是（）（）第七十七页，共一百四十三页，2022年，8月28日78推论3

在推论1的条件下，并设噪声服从正态分布，则最小误差方差估计是有效估计，即其中，M为Fisher信息矩阵。（）第七十八页，共一百四十三页，2022年，8月28日证明：和证明定理3类似，同类可以证明Markov参数估计将依概率1收敛于。则可得Fisher信息矩阵为与（）比较知，（）式成立。定理4和推论3表明，在一定条件下，最小二乘参数估计值和Markov参数估计值都是有效估计量。（）第七十九页，共一百四十三页，2022年，8月28日805.渐近正态性定理5

在推论2的条件下，设噪声服从正态分布，则最小二乘估计值服从正态分布，即

（）第八十页，共一百四十三页，2022年，8月28日81证明：根据及可得由知

可见，是的线性函数，则整理，即为（４０）式。（）（）（）第八十一页，共一百四十三页，2022年，8月28日82推论４在推论1的条件下，并设噪声服从正态分布，则最小误差方差估计服从正态分布。即（）第八十二页，共一百四十三页，2022年，8月28日834.7噪声方差估计

定理６：在推论2的条件下噪声方差的估计值由下式计算其中，为输出残差，即

（）第八十三页，共一百四十三页，2022年，8月28日84该定理提供了一种计算噪声方差估计值的方法。它必须先获得参数估计值，继而进一步求得输出残差然后按上式求的估计值。

而且是的无偏估计量。第八十四页，共一百四十三页，2022年，8月28日85证明是的无偏估计因，故Ｔ为同幂矩阵，，则（）（）（）第八十五页，共一百四十三页，2022年，8月28日86利用下列公式并考虑到是白噪声向量，它必与统计独立，则有（）第八十六页，共一百四十三页，2022年，8月28日87（）第八十七页，共一百四十三页，2022年，8月28日第八十八页，共一百四十三页，2022年，8月28日0.501.000.70-1.50真实参数0.41±0.610.98±0.610.74±0.02-1.48±0.075.00.46±0.140.93±0.120.66±0.06-1.47±0.061.00.48±0.070.96±0.060.67±0.03-1.48±0.040.50.49±0.020.99±0.010.69±0.01-1.50±0.010.10.50±0.001.00±0.000.70±0.00-1.50±0.000.00噪声均方差表

不同噪声水平下的辨识结果第八十九页，共一百四十三页，2022年，8月28日904.8最小二乘参数估计的递推算法

新的估计值=老的估计值+修正项

（）第九十页，共一百四十三页，2022年，8月28日91初值的选取（1）根据一批数据，利用一次完成算法，预先求得（2）直接给定初始值，a-充分大的实数，-充分小的实向量

（）第九十一页，共一百四十三页，2022年，8月28日最小二乘参数估计的递推算法目的：减小重复计算量和贮存空间、便于在线应用思想：按观测次序一步一修正，即

新的估计值=老的估计值+修正项改写一次性完成算法：(na+nb)

(na+nb)L

1(na+nb)1（）第九十二页，共一百四十三页，2022年，8月28日基于数据长度为L的测量值，所得参数最小二乘估计为：LL-1L-21PastFuture“估计”z(1)所用数据,这些数据构成h(1)︸max(na,nb)拍︸max(na,nb)拍“估计”z(L)所用数据,这些数据构成h(L)第九十三页，共一百四十三页，2022年，8月28日令k=L（即假设观测方程个数为k）,可得：其中：以下省去k(na+nb)L被称作记忆长度或数据长度（）（）（）第九十四页，共一百四十三页，2022年，8月28日第九十五页，共一百四十三页，2022年，8月28日进一步：重温可知(na+nb)

(na+nb)此k指观测数据长度（）（）（）第九十六页，共一百四十三页，2022年，8月28日这样：因为（）（）第九十七页，共一百四十三页，2022年，8月28日引进增益矩阵可得加权最小二乘的另一表述式：上式中除K(k)以外均为迭代计算形式。能否对K(k)，本质上是P(k),也实现迭代计算呢？

P(k)已经被定义为逆矩阵：欲实现其迭代计算，需用到矩阵反演公式。（）（）（）第九十八页，共一百四十三页，2022年，8月28日设A为nn非奇异阵，C为nm维矩阵，则有矩阵反演公式：两边同时右乘矩阵（A+CCT）可以证明上式是成立的。将改写为标量ACCTmmnn（）（）第九十九页，共一百四十三页，2022年，8月28日标量标量(na+nb)

(na+nb)与P(k-1)同维（）第一百页，共一百四十三页，2022年，8月28日（）（）（）第一百零一页，共一百四十三页，2022年，8月28日至此，可得加权最小二乘参数估计递推算法（RWLS-Recursive

WeightedLeastSquare）：新息时变矩阵对称阵（）第一百零二页，共一百四十三页，2022年，8月28日为了保证P(k)的对称性，有时将上式的第3式写成：这样在计算过程中即使有舍入误差，也能保证P(k)始终是对称的。（）第一百零三页，共一百四十三页，2022年，8月28日104初值的选取（1）根据一批数据，利用一次完成算法，预先求得（2）直接给定初始值，a-充分大的实数，-充分小的实向量

（）（）第一百零四页，共一百四十三页，2022年，8月28日因为根据参数估计公式有显然，使上式成立的条件是故有（）式（）（）第一百零五页，共一百四十三页，2022年，8月28日可用下式作为递推算法的终止条件

（）第一百零六页，共一百四十三页，2022年，8月28日例题考虑如图所示的仿真对象。图中v(k)是服从N(0,1)正态分布的不相关随机噪声输入信号u(k)采用4阶逆M序列，幅值为1。控制λ值，使数据的信噪比η=73%。++第一百零七页，共一百四十三页，2022年，8月28日选择如下模型结构加权因子取为Λ(k)=1，数据长度L=480；初始条件取为利用最小二乘递推算法在线估计参数，结果如表所示。第一百零八页，共一百四十三页，2022年，8月28日参数a1a2b1b2静态增益噪声均值噪声方差真值-1.50.71.00.57.50.01.0估计值-1.504240.7049091.043510.5116777.75001-0.000361451.00207为了进一步确认辨识结果，需要对所获得的模型进行检验。计算输出残差序列的均值和自相关系数，结果如下表。第一百零九页，共一百四十三页，2022年，8月28日均值ρ（0）1.0自相关系数ρ(l)=R(l)/R(0)ρ（1）-0.0525683ρ（6）-.0917693ρ（11）0.0115489ρ（16）-0.125323ρ（2）0.066278ρ（7）0.0260347ρ（12）-0.0456214ρ（17）0.0732433ρ（3）0.0515224ρ（8）-0.0136756ρ（13）-0.0409843ρ（18）-0.0173458ρ（4）-0.0854844ρ（9）0.0476114ρ（14）-0.0382442ρ（19）-0.0423732ρ（5）-0.0324464ρ（10）0.0392559ρ（15）0.0493622ρ（20）0.0307972上述结果表明，输出残差序列接近于白噪声，因此获得的模型是可靠的。第一百一十页，共一百四十三页，2022年，8月28日第一百一十一页，共一百四十三页，2022年，8月28日112几点讨论1.残差与新息的关系2.准则函数的递推计算3.递推算法的收敛性第一百一十二页，共一百四十三页，2022年，8月28日1131．残差与新息的关系新息描述时刻的输出预报误差残差用来描述时刻的输出偏差定义（）（）第一百一十三页，共一百四十三页，2022年，8月28日114残差与新息的之间存在以下联系或者

（）（）第一百一十四页，共一百四十三页，2022年，8月28日证明：根据残差、新息的定义和递推估计算法，有（）第一百一十五页，共一百四十三页，2022年，8月28日1162.准则函数的递推计算准则函数的递推计算为

采用上式计算准则函数，因为和在参数估计递推公式中已经求过了，可以直接利用，所以，递推计算准则函数速度非常快。（）第一百一十六页，共一百四十三页，2022年，8月28日1173.递推算法的收敛性如果噪声是零均值的白噪声那么6节中递推算法给出的参数估计值是一致收敛的

（）第一百一十七页，共一百四十三页，2022年，8月28日RWLS的收敛性对模型z(k)=hT(k)+n(k),若n(k)是均值为0的白噪声，可以证明WLS一次性估计算法是一致收敛的,即以概率1收敛于真值0。对RWLS算法，同样可以证明：（）第一百一十八页，共一百四十三页，2022年，8月28日证明：构造关于的差分方程，由于0是真值，故：得利用（）（）（）（）第一百一十九页，共一百四十三页，2022年，8月28日由于令故研究差分方程的稳定性问题：设矩阵A(k)的特征值为，则有

A(k)x=x其中x为非0特征向量（）（）（）（）第一百二十页，共一百四十三页，2022年，8月28日A(k)x=x{由于(k)>0且P-1(k-1)和h(k)(k)hT(k)为正定阵，故对所有非0向量x,(1-)和必须同号，即0<<1系统稳定（）（）（）（）（）（）第一百二十一页，共一百四十三页，2022年，8月28日递推最小二乘法的步骤用最初的组数据作矩阵及，求出参数的初始估计和作为初始值。求出。用新取得的观测数据，求出新的参数估计。继续进行新的采样，并从第2步开始重复第一百二十二页，共一百四十三页，2022年，8月28日从上述步骤可以看出，递推最小二乘初始值是用组数据求得的和，为此，必须求逆矩阵，比较麻烦。下面介绍一种简单的求初值的算法。在取得组数据后，可设第一百二十三页，共一百四十三页，2022年，8月28日仿真研究已知系统模型x(k)-1.5x(k-1)+0.7x(k-2)=2u(k-1)+0.5u(k-2),y(k)=x(k)+v(k),v(k)=αγ(k)，u、x、y、v分别为模型输入、模型输出、测量输出、干扰噪声。输入u为逆M序列：信号幅值a=1、寄存器位数为n=5(信号长度N=2n-1=31)第一百二十四页，共一百四十三页，2022年，8月28日α为噪信比调整因子，噪信比定义为：、分别为模型输出x和噪声v的均方差（标准差），γ有两种模型：(1)γ为白噪声，(2)γ为有色噪声，噪声模型为：γ(k)=e(k)+0.5e(k-1)+0.9γ(k-1)-0.95γ(k-2)e(k)为白噪声第一百二十五页，共一百四十三页，2022年，8月28日定义辨识误差值：其中：Ｎ为独立的实验次数,为模型真值为模型估计值第一百二十六页，共一百四十三页，2022年，8月28日选择自相关特性好的M序列作为输入。利用MATLAB产生寄存器位数n=5，每周期长为31，重复周期数q=40的M序列，并将其作为输入得到系统输出。绘出一个周期的输入输出图形分别如图2和图3所示。第一百二十七页，共一百四十三页，2022年，8月28日产生系统噪声为了后面能较好的区分每种辨识方法的性能，我们分别在输出中叠加白噪声和有色噪声。取NSR=20%，用同一噪声源产生两种噪声模型，分别绘制白噪声、用相同噪声模型产生的有色噪声和不同噪声影响下的系统输出的曲线。第一百二十八页，共一百四十三页，2022年，8月28日第一百二十九页，共一百四十三页，2022年，8月28日最小二乘辨识模型辨识

为较好的研究最小二乘辨识模型的性能，分别在不同的噪声模型下，用不同的噪信比影响系统输出，利用输入输出数据对系统进行辨识。ν分别采用白噪声模型和有色噪