第二章特殊三角形整章复习杨秀兰未定稿

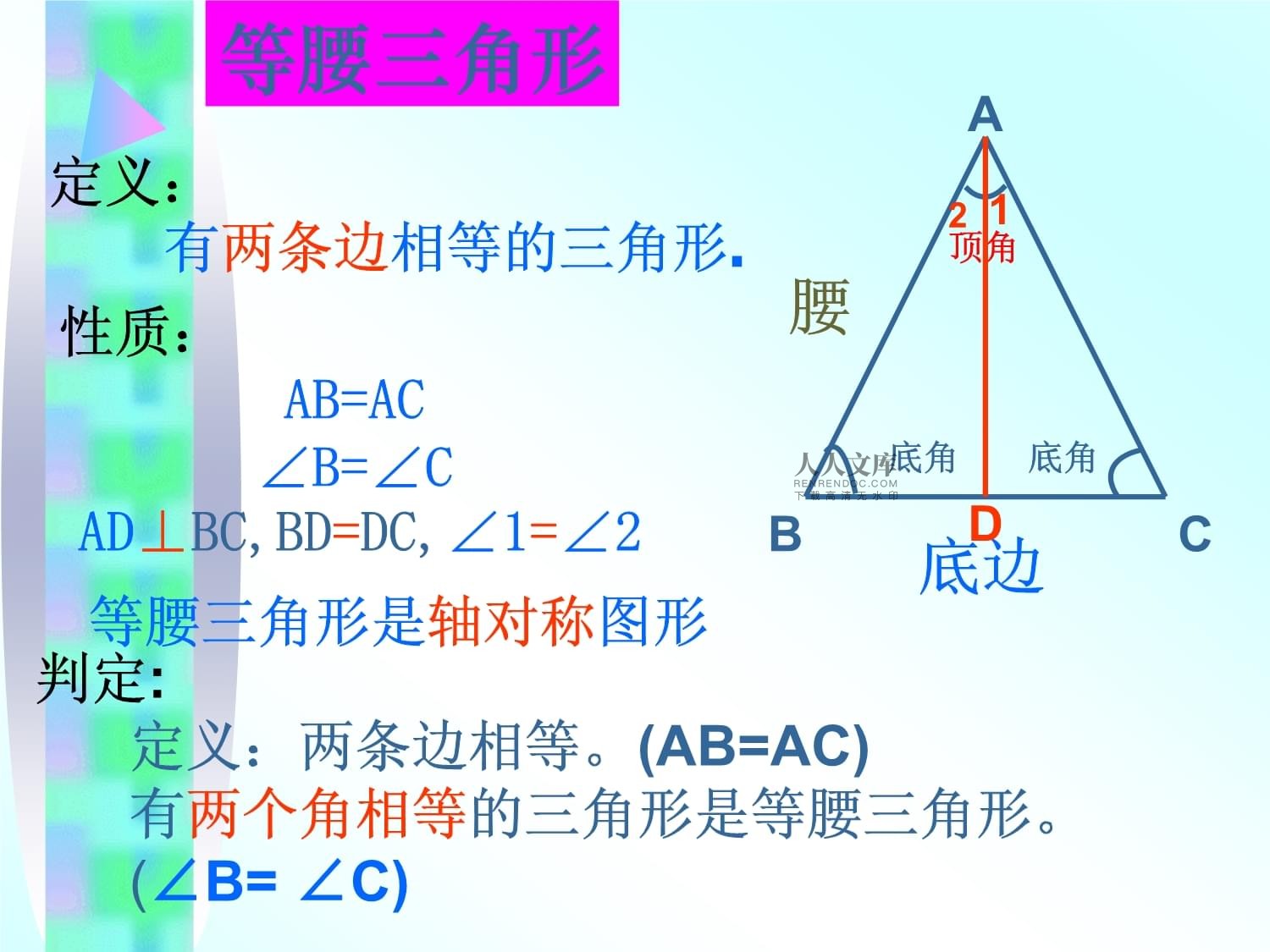
特殊三角形复习腰底边底角底角顶角ABC定义：有两条边相等的三角形.性质：

AB=AC∠B=∠C

D12AD⊥BC,BD=DC,∠1=∠2等腰三角形判定:

定义：两条边相等。(AB=AC)

有两个角相等的三角形是等腰三角形。

(∠B=∠C)等腰三角形是轴对称图形1.在△ABC中,AB=AC,∠A=70°,那么∠C=______.4.在△ABC中,AC=AB,AD是△ABC的角平分线,已知BC=7,∠B=63°.则BD=______,∠ADB=______,∠BAC=______.55°2.等腰三角形顶角和一个底角之和为100°，则顶角度数为_____________。3.等腰三角形两边长为4、6，这个三角形周长为___________。20°14或163.590°54°热身练习定义：有两条边相等的三角形是等腰三角形.性质1：等腰三角形的两个底角相等。（角）性质2：等腰三角形的两腰相等。（边）性质3：等腰三角形的三线合一。（内部线）5.在△ABC中,AC=AB=BC,则△ABC是（）三角形等边ABC定义：三条边都相等的三角形性质：

AB=AC＝BC∠B=∠C=∠A=60°

三个三线合一判定：

AB=AC＝BC∠B=∠C=∠A=60°

有一个角是60°的等腰三角形。等边三角形（正三角形）1、满足下列条件的三角形不一定是等边三角形的是（）（A）在△ABC中，AB=BC=AC（B）在△ABC中，∠A=∠B=60°（C）在△ABC中，AB=BC，∠A=60°（D）在△ABC中，∠A=60°

D巩固一练例1.等腰三角形两个内角之比为4:1，求顶角的度数.例题分析说明:

因为等腰三角形的两底角相等,两个内角的比为4:1,尚未指明哪两个角,可能是顶角与底角的比,也可能是底角与顶角的比,所以分两种情况求解.

此类题未说明哪两个角的比,解题时应审清题意,注意分类讨论.例2.如图，已知在△ABC中，AB=AC，BD⊥AC

于D，CE⊥AB于E，BD与CE相交于M点。

求证：BM=CM。说明：本题易习惯性地用全等来证明，虽然也可以证明，但过程较复杂，应当多加强等腰三角形的性质和判定定理的应用。例题分析证明：∵AB=AC∴∠ABC=∠ACB

（在同一个三角形中等边对等角）∵BD⊥AC于D，CE⊥AB于E∴∠BEC=∠CDB=90°∴∠1+∠ACB=90°，∠2+∠ABC=90°

（直角三角形两个锐角互余）∴∠1=∠2（等角的余角相等）∴BM=CM

（在同一个三角形中等角对等边）例3.如图，在等边△ABC中，AF=BD=CE，

请说明△DEF也是等边三角形的理由.解：∵△ABC是等边三角形∴AC=BC，∠A=∠C∵CE=BD∴BC－BD=AC－CE即∴CD=AE在△AEF和△CDE中∴△AEF≌△CDE（SAS）∴EF=DE同理可证EF=DF∴EF=DE=DF∴△DEF是等边三角形说明：证明等边三角形有三种思路：①证明三边相等 ②证明三角相等③证明三角形是有一个角为60°的等腰三角形。具体问题中可利用不同的方式进行思考求解。例题分析例4.已知等腰三角形一腰上的中线将三角形周长分成2:1两部分，已知三角形底边长为5，求腰长？解：如图，令CD＝x，则AD＝x，AB＝2x∵底边BC＝5∴BC＋CD＝5＋x

AB＋AD＝3x∴(5+x)：3x＝2:1或3x：(5+x)=2:1ＡＢＣＤxx2x5例题分析小结1、等腰三角形的有关概念。2、等腰三角形的识别。3、应用等腰三角形的性质定理和三线合一性质解决有关问题。4、通过习题，能总结代数法求几何角的大小、线段长度的方法。C如图,在ΔABC中∠C=90度∠A=30°，则∠B=______BC=1，则AB的长为______CD是斜边AB的中线，则CD的长为______则AC的长为______CE是斜边AB的高线，则CE的长为______

60°2

1ABDE热身练习30°EEEABDE有一个角为直角角：直角三角形两锐角互余；线：直角三角形斜边上的中线等于斜边的一半；边：直角三角形两直角边的平方和等于斜边的平方.（勾股定理）回顾直角三角形的性质特殊直角三角形：在直角三角形中，如果有一个锐角等于30°,那么这个角所对的直角边是斜边的一半.直角三角形从角的方面：从边的方面：两锐角互余，即∠A+∠B=90°D直角三角形，斜边上的中线等于斜边的一半。直角三角形，两直角边的平方和等于斜边的平方abc可逆可逆可逆定义：有一个角是直角的三角形性质：Rt△ABC中,∠C=Rt∠，∠A:

∠B=2:1,

则∠ACD=______.∠BCD=______.ACB30°60°2.已知一个三角形的三个内角之比为1：1：2，求这个三角形的三个内角的度数，并说明是什么形状的三角形。等腰直角三角形ACB3.已知Rt△ABC中，斜边上的中线CD=5cm，则斜边AB=________.

(1)若∠A=30°，则BC=________.D105

(2)若∠ADC=130°，则∠B=________.65°

(3)若AC=8，则BC=________.6直角三角形斜边上的中线ACBD直角三角形斜边上的高线4.如图,Rt△ABC中,∠C=Rt∠，CD⊥AB,(1)若∠A=37°,则∠BCD=_____.(2)若AC=3,BC=4,则CD=_____.37°2.4勾股定理及其逆定理5、以下列线段为边长能构成一个直角三角形的是（）（A）1，2，3（B）2，3，4（C）6，8，10（D）4，5，6CABCD6.已知△ABC中，AB=AC=4.AD⊥BC,AD=3cm，则BC=________.7.已知△ABC中，∠ACB=Rt.CD⊥AB,BC=5cm，CD是斜边AB上的中线，CE=,则AB=________,AC=________,CD=________.

1312直角三角形全等的判定方法：ABCA′B′C′ASA,AAS2)SAS3)SSS4)HL直角三角形特殊的全等判定方法“HL8.如图，AC与BD相交于点O，已知AD⊥BD，BC⊥AC,AC=BD,则OA=OB请说明理由。

能否找到这两边所在的两个三角形？已知，如图AC=BD，AD⊥BDBC⊥AC，试说明AD＝BC.DABC要说明AD＝BC是否能找到这两边所在的两个三角形？Ｏ△AOD≌△BOC？连结AB例1还有哪些线段相等?变式一:如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由。变式二：如图，已知AG⊥BD，AC⊥BG

，E是AB的中点，F是CD的中点，则EF⊥CD，请说明理由。ABDCGEFFEDBCA如图，长方形ABCD中，把△ABE沿着AE折叠使得B点落在F点，AD=8,AB=10,则求(1)CF的长,(2)CE的长

∴解这个方程，16x=48x=3∴CE=3（cm）方程思想的应用解(1)由题意可知：AF=AB=10AD=8在Rt△ADF中：DF=6

∴

CF=10-6=4（cm）(2)设CE=x,则EF=BE=8-x，在RT△ECF中：EF2=CF2+CE2(8-x)2=42+x2例2已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为多少？ABEFDC思路：找出不变量，分析问题的数量关系，通过已知和未知的联系，建构方程，最后解出方程变式1G1、满足下列条件的ΔABC，不是直角三角形的是：（）

A、b2=a2-c2B、∠C=∠A-∠B

C、∠A：∠B：∠C=3：4：5D、a:b:c=12:9:15

2、下列条件中，不能判定两个直角三角形全等的是：（）

A、一条直角边和一个锐角分别相等

B、两条直角边对应相等

C、斜边和一条直角边对应相等

D、斜边和一个锐角对应相等

AC练一练15、在△ABC中，AB=AC=10，BC=12，则△ABC的面积=__________。2416.在直角三角形中，斜边与较小直角边的和、差分别是8、2，则较长的直角边长为__________.422、如图，在Rt△ABC中，∠A=90°，BC=10，分别以AB、AC为直径向外做半圆，求这三个半圆的面积之和。4、如图，某校A与公路距离为3000米，又与该公路旁上的某车站D的距离为5000米，现要在公路边建一个商店C，使之与该校A及车站D的距离相等，则商店与车站的距离约为（）（A）875米（B）3125米（C）3500米（D）3275米CDA3、如图，一个长为25分米的梯子，斜立在一竖直的墙上，这时梯足距墙底端7分米，如果梯子的顶端沿墙下滑4分米。那么梯足将滑（）（A）15分米（B）9分米（C）8分米（D）5分米CA思考：若A城与B地的方向保持不变，为了确保A城不受台风

影响至少离B地多远？解：作AD⊥BF∵由已知可得：∠

FBA=300∴AD=1/2AB=150KM

而150＜200

所以A城会受到台风的影响例1。如图，设A城市气象台测得台风中心，在A城正西方向300千米的B处，正向北偏东600的BF方向移动，距台风中心200千米的范围内是受台风影响的区域，那么A城是否受到这次台风的影响？为什么？如果你是气象员，请你算一算。东北FBA600D应用与延伸例2、如图，已知AB=AD，CB=CD，AC，BD相交于点O，若AB=5，AC=7，BD=6,求∠BCD的度数解：∵AB=AD∴点A在线段BD的中垂线上同理点也在BD的中垂线上∴AC⊥BD且平分BD∵BD=6∴BO=3∵AB=5由勾股定理得AO=4∵AC=7∴OC=3∴△BOC等腰直角三角形∴∠BCO=45°同理∠DCO=45°∴∠BCD=90°ABDCO例3、如图，已知四边形ABCD中，∠B=90°AB=4，

BC=3,AD=12，DC=13，求四边形ABCD的面积ABCDABCDE3、如图已知四边形ABCD中，∠A=60°∠B=∠D=90°，BC=3，CD=2，求的值2AB解:连接AC∵∠B=90°,AB=4,BC=3∴AC=5∵AD=12,DC=132AC2AD+=2CD∴∠CAD=90°S四边形ABCD=×3×4＋×5×12=3621_21_21_解：延长AD、BC交于E∵∠A=60°，∠B=∠D=90°∵∠C=30°CD=CE，CD=2∴CE=4，又BC=3∴BE=7，由勾股定理得∴AB=21_AE，2AB2BE+=2AB42AB=49—3在直角三角形中，斜边上的中线长为１，周长为２＋，求此直角三角形的面积。提高题ＡＣＢＤ1、通过这节课的复习，你对直角三角形的知识有进一步的了解吗？又学到了关于它的哪些知识呢？2、(1),每位同学自编一道题目，能够运用有关直角三角形的知识进行解答，然后同桌之间交换解题。

(2).完成作业本上小结.课堂小结和作业巩固练习1.

下列结论叙述正确的个数为（）（1）等腰三角形高、中线、角平分线重合；（2）等腰三角形两底角的外角相等；

（3）等腰三角形有且只有一条对称轴；（4）有一个角等于60°的等腰三角形是等边三角形。（A）0个（B）1个（C）2个（D）3个c2.如图，在△ABC中，AB=AC，∠1=∠2，则AD平分∠BAC，请说明理由。3.如图，在△ABC中，∠ABC和∠ACB的平分线相交于F，过点F作DE//BC,交AB于点D，交AC于点E，若DB=5，EC=4，求线段DE的长。4.已知一腰和底边上的高，求作等腰三角形。分析：我们首先在草稿上画好一个示意图，然后对照此图写出已知和求作并构思整个作图过程……已知：线段a、h求作：△ABC，使AB=AC=a，高AD=h作法：1、作PQ⊥MN，垂足为D2、在DM上截取DA=h3、以点A为圆心，以a为半径作弧，交PQ于点B、C4、连结AB、AC则△ABC为所求的三角形。5.已知△ABC中AB=AC，AB垂直平分线交AC于E，交AB于D，连结BE，若∠A=50°，∠EBC=__________。6.△ABC中，AB=AC，AD⊥BC于D，若△ABC的周长为50，△ABD的周长为40，则AD=____________。7.若等腰三角形顶角为n度，则腰上的高与底边的夹角为_____________。

7.如图，线段OD的一个端点O在直线a上，以OD为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能画多少个?ＯＤ150°⌒ＣaＥＦＨ8、如图，D是正△ABC边AC上的中点，E是BC延长线上一点，且CE=CD，请说明BD=DE的理由.ABCED12解:∵△ABC是正三角形

∴∠ABC=∠ACB=600

（）

∵

D是AC边上的中点∴∠1=∠ABC=300（）∵CE=CD∴∠2=∠E（）∵∠2+∠E=∠ACB=600（）∴∠E=300，∴∠1=∠E∴BD=DE（）9.已知：如图，∠C=90°，BC=AC，D、E分别在BC和AC上，且BD=CE，M是AB的中点.

求证：△MDE是等腰三角形.分析：要证△MDE是等腰三角形，只需证MD=ME。连结CM，可利用△BMD≌△CME得到结果。证明：连结CM∵∠C=90°，BC=AC∴∠A=∠B=45°∵M是AB的中点∴CM平分∠BCA（等腰三角形顶角的平分线和底边上的中线重合）∴∠MCE=∠MCB=∠BCA=45°∴∠B=∠MCE=∠MCB∴CM=MB（等角对等边）在△BDE和△CEM中∴△BDM≌△CEM（SA