高等数学经管类专升本 第一章 向量

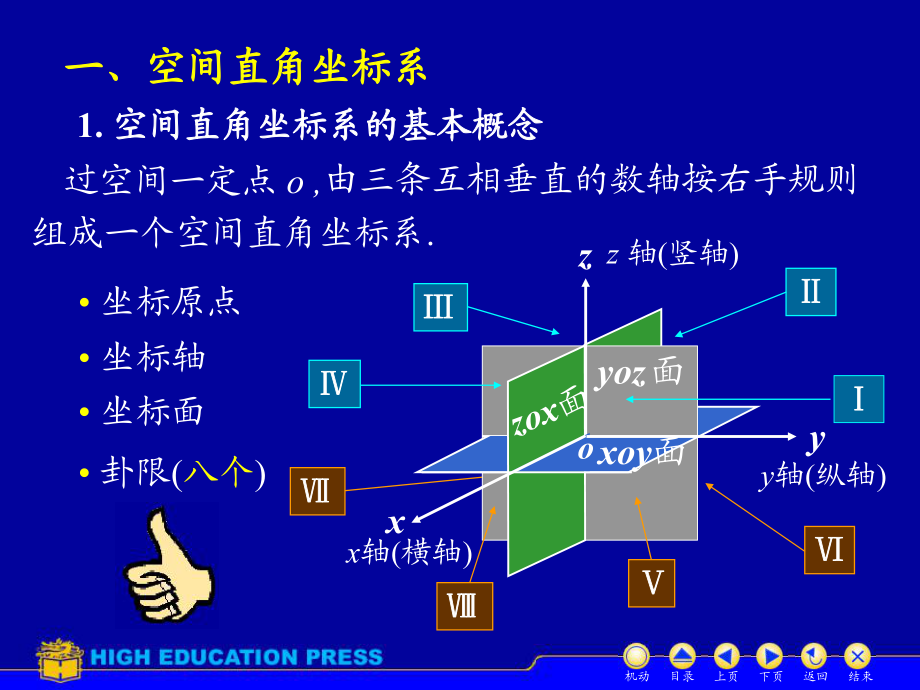
1、数量关系数量关系 第一章第一部分第一部分 向量代数向量代数第二部分第二部分 空间解析几何空间解析几何 在三维空间中:空间形式空间形式 点点, , 线线, , 面面基本方法基本方法 坐标法坐标法; ; 向量法向量法坐标坐标, , 方程（组）方程（组）向量与空间解析几何 四、空间直线方程四、空间直线方程一、空间直角坐标系一、空间直角坐标系二、向量及其运算二、向量及其运算 三、空间平面方程三、空间平面方程五、曲面方程五、曲面方程 机动 目录 上页 下页 返回 结束 第一一章 六、曲线方程六、曲线方程 xyz一、空间直角坐标系一、空间直角坐标系由三条互相垂直的数轴按右手规则组成一个空间直角坐标系. 坐

2、标原点 坐标轴x轴(横轴)y轴(纵轴)z 轴(竖轴)过空间一定点 o ,o 坐标面 卦限(八个)面xoy面yozzox面1. 空间直角坐标系的基本概念空间直角坐标系的基本概念机动 目录 上页 下页 返回 结束 坐标轴 : 轴x00zy00 xz轴y轴z00yx坐标面 :面yox0 z面zoy0 x面xoz0 y机动 目录 上页 下页 返回 结束 xyzo两点间的距离公式:222212121()()()ABxxyyzz记作:模 : 向量的大小,21MM记作二、向量二、向量1.向量:(又称矢量). 1M2M既有大小, 又有方向的量称为向量单位向量: 模为 1 的向量,.aa记记作作或或有向线段 M

3、1 M2 ,或 a ,a或.a或机动 目录 上页 下页 返回 结束 a .或或若向量 a 与 b 方向相同或相反, ab ;平行向量:2、向量的加法、向量的加法三角形法则:平行四边形法则:运算规律 : 交换律结合律机动 目录 上页 下页 返回 结束 bbabbacba )()(cbacbaaaba ba 向量的减法向量的减法ab)( abaa3. 向量与数的乘法向量与数的乘法.a 规定 :时，0，同向与aa,0时,0时.0a;aa;aa，反向与aa总之:运算律 : 结合律)(a)(aa分配律a)(aa)(baba且且有有单单位位向向量量01.aaa 机动 目录 上页 下页 返回 结束 4. 向

4、量的坐标表示向量的坐标表示, ),(zyxM则沿三个坐标轴方向的分向量分向量.rOMxiy jzk ( , , )x y z xoyzMNBCijkA,轴上的单位向量分别表示以zyxkji设点 M的坐标为rkzjyix称为向量,rNMONOMOCOBOA机动 目录 上页 下页 返回 结束 , ixOA, jyOBkzOC,x y zr称称为为向向量量沿三个坐标轴方向的投影投影.5、向量运算的坐标表示、向量运算的坐标表示设设),(zyxaaaa , ),(zyxbbbb 则则ba),(zzyyxxbababaa(,),xyzaaa/yzxxyzbbbabbaaaa(4) 平行向量对应坐标成比例平

5、行向量对应坐标成比例:，为实数机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 (1)(2)(3) 设点设点11112222(,),(,),MxyzMxyz则向量则向量11112222,OMxyzOMxyz 12212121,M Mxxyyzz222xyzaaaaoyzx6. 向量的方向余弦向量的方向余弦aOAB),(ab或,0),(zyxr给定与三坐标轴的夹角与三坐标轴的夹角 , , rr称为其为其方向角方向角. 方向角的余弦称为其方向角的余弦称为其方向余弦方向余弦. 记作记作),(ba机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 b ba,的夹角的夹角: 222co

6、syyxyzaaraaa 222cosxxxyzaaraaa 222coszzxyzaaraaa 注注:机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 222(1)coscoscos1,01(2)cos ,cos,cos .aaa1M7、向量的数量积、向量的数量积(1) 定义定义: (点积点积) FcosWFs 2Ms机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 引例引例F scosa ba b (2) 性质性质202221 :,xyza aaaaa 02 :,xxyyzza ba ba ba b 2022222,3 :cosxxyyzzxyzxyza ba ba b

7、a ba baaabbb 0004 :xxyyzzaba ba ba ba b 。(3) 运算律运算律交换律交换律结合律结合律abbaba)()( ba)(ba)()(ba)(ba)(ba分配律分配律cbcacba机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 例例1. 求与两点)7, 1 ,4(A等距离的点轨迹.解解: 设该点为( , , ),M x y z,BMAM因为222222(4)(1)(7)(3)(5)(2)xyzxyz解得749140 xyz及)2,5,3(B机动 目录 上页 下页 返回 结束 （垂直平分面）（垂直平分面）例例2. 已知两点)5,0,4(A和, )3,

8、 1 ,7(B解解:求141)2,1,3(142,141,143.BABABABA例例3. 已知两点)2,2,2(1M和, )0,3, 1(2M的模 、方向余弦和方向角 . 解解:,21,23)20计算向量)2, 1, 1(222)2(1) 1(2,21cos,21cos22cos,32,34321MM(21MM21MM机动 目录 上页 下页 返回 结束 解解: 因例例5. 设,853kjim求其在 x 轴上的投影及在 y轴上的分向量.3xa 在 y 轴上的分向量为5ya jj 故在 x 轴上的投影为机动 目录 上页 下页 返回 结束 ,853kjim且垂直于非零向量且垂直于非零向量000()

9、()()0A xxB yyC zz的平面的平面 的的方程为方程为法向量法向量. .(,)nA B C 的为平面称n三、平面方程三、平面方程1 1、点法式方程、点法式方程0000(,)Mxyz平平面面过过2 2、一般式方程、一般式方程+0AxByCz D注：注：(1)(1) D = 0平面过原点平面过原点；(2) A = 0(3) A = 0，B = 0 平面平行于平面平行于xoy面；面；平面平行于平面平行于x轴；轴；(4) A = 0，D = 0 平面过平面过x轴轴.例例1. 求通过 x 轴和点( 4, 3, 1) 的平面方程.解解: 因平面通过 x 轴 ,0 DA故设所求平面方程为0zCyB

10、代入已知点) 1,3,4(得BC3化简,得所求平面方程03 zy机动 目录 上页 下页 返回 结束 因此有例例2. 一平面通过两点垂直于平面: x + y + z = 0, 求其方程 .解解: 设所求平面的法向量为,020CBA即CA2的法向量,0CBACCAB)()0(0) 1() 1() 1(2CzCyCxC约去C , 得0) 1() 1() 1(2zyx即02zyx0) 1() 1() 1(zCyBxA)1, 1, 1(1M, )1, 1,0(2M和则所求平面故, ),(CBAn方程为 n21MMn且机动 目录 上页 下页 返回 结束 四、空间直线方程四、空间直线方程1111222200

11、A xB yC zDA xB yC zD 因此其一般式方程因此其一般式方程1 1. 一般式方程一般式方程 直线可视为两平面交线，直线可视为两平面交线，机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 且平行于非零向量且平行于非零向量000 xxyyzzmnp的直线的直线 l 的的方程为方程为(,)sm n p 2 2、点向式方程、点向式方程0000(,)Mxy z直直线线过过t 3 3、参数式方程、参数式方程000 xxmtyymtzzmt 注注:1212121212(1)0LLssm mn np p机动 目录 上页 下页 返回 结束 1111212222(2)/mnpLLssmnp

12、(3)/Lsn (4)/Lsn 解解: : 取已知平面的法向量421zyx则直线的对称式方程为0432zyx直的直线方程. 为所求直线的方向向量. 132垂 ) 1,3,2(nn例例1. 求过点(1,2 , 4) 且与平面机动 目录 上页 下页 返回 结束 例例2. 2. 求过求过解解: 令交点为令交点为由于由于从而从而L方程为方程为则则L方向向量为方向向量为0(3 ,57,22)Pttt(2,1, 3)P 且与直线且与直线垂直相交的直线垂直相交的直线L方程方程. .172:352xyzL032,56,21;sPPttt 1,LL 所以所以10s s ，故故3(32)5(56)2(21)0tt

13、t得得1t 则交点为则交点为0(3, 2,4)P ，213.111xyz 又又1, 1,1,s P1LL0P五、曲面方程五、曲面方程求到两定点A(1,2,3) 和B(2,-1,4)等距离的点的222)3()2() 1(zyx07262zyx化简得即说明说明: 动点轨迹为线段 AB 的垂直平分面.引例引例: :显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程.222)4() 1()2(zyx解解: :设轨迹上的动点为, ),(zyxM,BMAM 则轨迹方程. 机动 目录 上页 下页 返回 结束 定义定义1. 0),(zyxFSzyxo如果曲面 S 与方程 F( x, y

14、, z ) = 0 有下述关系:(1) 曲面 S 上的任意点的坐标都满足此方程;则 F( x, y, z ) = 0 叫做曲面曲面 S 的的方程方程, (2) 不在曲面 S 上的点的坐标不满足此方程,例例1. 求动点到定点求动点到定点0000(,)Mxy z距离为距离为 R 的轨迹方程的轨迹方程.( , , ),M x y z解解: 设轨迹上动点为设轨迹上动点为xyzoM0M2220000()()()MMxxyyzzR2202020)()()(Rzzyyxx(球面球面)(一一) 曲面定义曲面定义 xyz( (二二) )柱面柱面引例引例. . 分析方程分析方程的坐标也满足方程的坐标也满足方程22

15、2xyR解解: :在在 xoy 面上面上，表示圆表示圆C, 222xyR222xyR沿曲线沿曲线C平行于平行于 z 轴的一切直线所形成的曲面轴的一切直线所形成的曲面称为称为圆柱面圆柱面. .过此点作过此点作对任意对任意 z ,平行平行 z 轴的直线轴的直线 l ,oC在圆在圆C上任取一点上任取一点 1( , ,0),Mx ylM1M( , , )M x y z点点定义定义2.平行定直线并沿定曲线平行定直线并沿定曲线 C 移动的直线移动的直线l 形成的轨迹叫做形成的轨迹叫做柱面柱面.C 叫做叫做准线准线, l 叫做叫做母线母线.lCxyzxyzo如 表示抛物柱面抛物柱面,母线平行于 z 轴;准线

16、为xoy 面上的抛物线. z 轴的椭圆柱面椭圆柱面.xy2212222byax表示母线平行于o机动 目录 上页 下页 返回 结束 定义定义3. . 一条平面曲线( (三三) )旋转曲面旋转曲面 绕其平面上一条定直线定直线旋转一周所形成的曲面叫做旋转曲面旋转曲面.该定直线称为旋转旋转轴轴 . .例如例如 :机动 目录 上页 下页 返回 结束 注：注：故旋转曲面方程为故旋转曲面方程为, ),(zyxM当绕当绕 z 轴旋转时轴旋转时, ,0),(11zyf,), 0(111CzyM若点若点给定给定 yoz 面上曲线面上曲线 C: ), 0(111zyM),(zyxM1221,yyxzz则有则有22(

17、, )0fxyz则有则有该点转到该点转到0),(zyfozyxC机动机动 目录目录 上页上页 下页下页 返回返回 结束结束 给定给定yoz面上曲线面上曲线C 绕绕 z 轴旋转所成曲面轴旋转所成曲面的的方程方程:例例1. 试求yoz面上直线所得曲面方程. 解解:(0)zky k2222()zkxyxyzL), 0(zyM机动 目录 上页 下页 返回 结束 绕z轴旋转一周22(, )0fxyz-圆锥面圆锥面xy例例2. 求坐标面 xoz 上的双曲线12222czax分别绕 x轴和 z 轴旋转一周所生成的旋转曲面方程. 解解: :绕 x 轴旋转122222czyax绕 z 轴旋转122222czay

18、x这两种曲面都叫做旋转双曲面.所成曲面方程为所成曲面方程为z机动 目录 上页 下页 返回 结束 (双叶)(单叶)注：注： 常见二次曲面常见二次曲面2222221xyzabc(1)(1)222xyR 2222000()()()xxyyzzR22()za xy（球面）（球面）2222()zaxy(2)(2)(3)(3)(5)(5)(4)(4)（椭球面）（椭球面）（锥面）（锥面）（旋转抛物面）（旋转抛物面）（圆柱面）（圆柱面）作图作图：(1)(1)22,1zxyz所围成的曲面，所围成的曲面，(2)2222,1zxyzxy所围成的曲面，所围成的曲面，六、空间曲线六、空间曲线1. 一般方程 空间曲线可视为两曲面的交线,( , , )0( , , )0F x y zG x y z 2SL0),(zyxF0),(zyxG1S例如例如,方程组632122zxyx表示圆柱面与平面的交线 C. xzy1oC2机动 目录 上页 下页 返回 结束 六、空间曲线六、空间曲线(一)曲线方程zyxo将曲线C上的动点坐标x, y, z表示成参数t 的函数:称它为空间曲线的参数方程.)(txx 例如,圆柱螺旋线vbt,令bzayaxsincostaxcostaysin t vz 的参数方程为)(tyy )(tzz M机动 目录 上页 下页 返回 结束 2.参数方程设空间曲