正交试验设计

1、正交试验设计法正交试验设计法的基本思想正交表正交表试验方案的设计试验数据的直观分析正交试验的方差分析补充内容1.正交试验设计法的基本思想正交试验设计法，就是使用已经造好了的表格-正交表-来安排试验并进行数据分析的一种方法。它简单易行，计算表格化，使用者能够迅速掌握。下边通过一个例子来说明正交试验设计法的基本想法。例1为提高某化工产品的转化率，选择了三个有关因素进行条件试验，反应温度(A),反应时间(B),用碱量(C),并确定了它们的试验范围：A: 80-90CB: 90-150分钟C: 5-7%试验目的是搞清楚因子ABC对转化率有什么影响，哪些是主要的，哪些是次要的，从而确定最适生产条件，即温

2、度、时间及用碱量各为多少才能使转化率高。试制定试验方案。这里，对因子A,在试验范围内选了三个水平；因子B和C也都取三个水平：A: Al=80C,A2=85C,A3=90CB: Bl=90分，B2=120分，B3=150分C: Cl=5%,C2=6%C3=7%当然，在正交试验设计中，因子可以是定量的，也可以是定性的。而定量因子各水平间的距离可以相等，也可以不相等。这个三因子三水平的条件试验，通常有两种试验进行方法：(I)取三因子所有水平之间的组合，即A1B1C1,A1B1C2,A1B2C1，A3B3C3共有33=27次试验。用图表示就是图1立方体的27个节点。这种试验法叫做全面试验法。全面试验对

3、各因子与指标间的关系剖析得比较清楚。但试验次数太多。特别是当因子数目多，每个因子的水平数目也多时。试验量大得惊人。如选六个因子，每个因子取五个水平时，如欲做全面试验，则需56=15625次试验，这实际上是不可能实现的。如果应用正交实验法，只做25次试验就行了。而且在某种意义上讲，这25次试验代表了15625次试验。图1全面试验法取点(H)简单对比法，即变化一个因素而固定其他因素，如首先固定B、C于Bl、Cl,使A变化之：/A1B1C1-A2A3(好结果)如得出结果A3最好，则固定A于A3,C还是Cl,使B变化之：/B1A3C1-B2(好结果)B3得出结果以B2为最好，则固定B于B2,A于A3,

4、使C变化之：/C1A3B2C2(好结果)C3试验结果以C2最好。于是就认为最好的工艺条件是A3B2C2这种方法一般也有一定的效果，但缺点很多。首先这种方法的选点代表性很差，如按上述方法进行试验，试验点完全分布在一个角上，而在一个很大的范围内没有选点。因此这种试验方法不全面，所选的工艺条件A3B2c如一定是27个组合中最好的。其次，用这种方法比较条件好坏时，是把单个的试验数据拿来，进行数值上的简单比较，而试验数据中必然要包含着误差成分，所以单个数据的简单比较不能剔除误差的干扰，必然造成结论的不稳定。简单对比法的最大优点就是试验次数少，例如六因子五水平试验，在不重复时，只用5+(6-1)X(5-1

5、)=5+5X4=25次试验就可以了。考虑兼顾这两种试验方法的优点，从全面试验的点中选择具有典型性、代表性的点，使试验点在试验范围内分布得很均匀，能反映全面情况。但我们又希望试验点尽量地少，为此还要具体考虑一些问题。如上例，对应于A有Al、A2、A3三个平面，对应于B、C也各有三个平面，共九个平面。则这九个平面上的试验点都应当一样多，即对每个因子的每个水平都要同等看待。具体来说，每个平面上都有三行、三列，要求在每行、每列上的点一样多。这样，作出如图2所示的设计，试验点用。表示。我们看到，在9个平面中每个平面上都恰好有三个点而每个平面的每行每列都有一个点，而且只有一个点，总共九个点。这样的试验方案

6、，试验点的分布很均匀，试验次数也不多。当因子数和水平数都不太大时，尚可通过作图的办法来选择分布很均匀的试验点。但是因子数和水平数多了，作图的方法就不行了。试验工作者在长期的工作中总结出一套办法，创造出所谓的正交表。按照正交表来安排试验，既能使试验点分布得很均匀，又能减少试验次数，图2正交试验设计图例而且计算分析简单，能够清晰地阐明试验条件与指标之间的关系。用正交表来安排试验及分析试验结果，这种方法叫正交试验设计法。2.正交表本书附录给出了常用的正交表。为了叙述方便，用L代表正交表，常用的有L8(27),L9(34),L16(45),L8(4X24),L12(211),等等。此符号各数字的意义如

7、下：L8(27)7为此表列的数目(最多可安排的因子数)2为因子的水平数8为此表行的数目(试验次数)L18(2X37)有7列是3水平的有1列是2水平的L18(2X37)的数字告诉我们，用它来安排试验，做18个试验最多可以考察一个2水平因子和7个3水平因子。在行数为mn型的正交表中(m,n是正整数)，试验次数(行数)=2(每列水平数-1)+1(1)如L8(27),8=7X(2-1)+1利用上述关系式可以从所要考察的因子水平数来决定最低的试验次数，进而选择合适的正交表。比如要考察五个3水平因子及一个2水平因子，则起码的试验次数为5X(3-1)+1X(2-1)+1=12(次)这就是说，要在行数不小于1

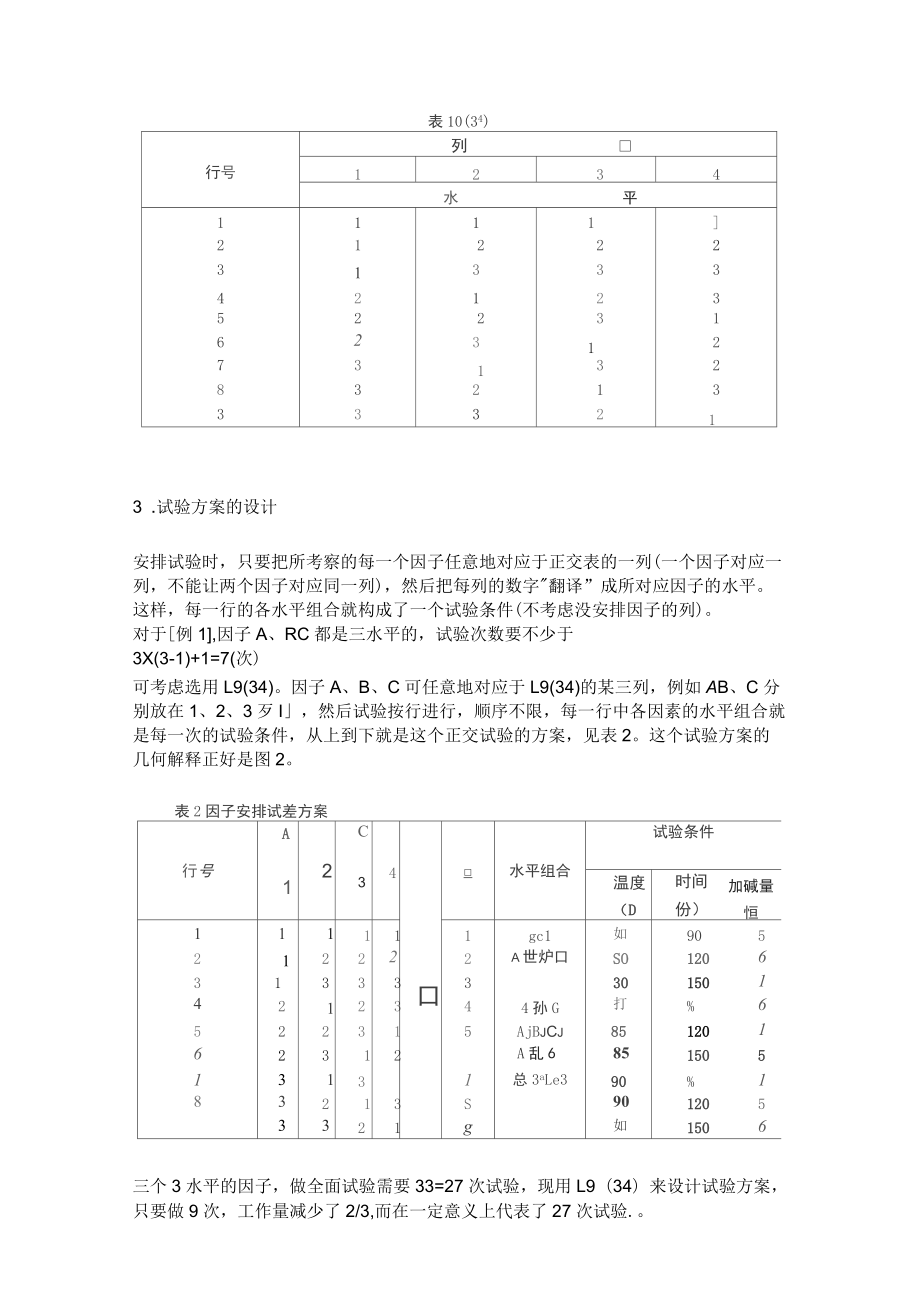
8、2,既有2水平列又有3水平列的正交表中选择，L18(2X37)适合。正交表具有两条性质：(1)每一列中各数字出现的次数都一样多。(2)任何两列所构成的各有序数对出现的次数都一样多。所以称之谓正交表。例如在L9(34)中(见表1),各列中的1、2、3都各自出现3次；任何两列，例如第3、4歹I，所构成的有序数对从上向下共有九种，既没有重复也没有遗漏。其他任何两列所构成的有序数对也是这九种各出现一次。这反映了试验点分布的均匀性。表10(34)列行号1234水平111121222313334212352231623127313283213333213 .试验方案的设计安排试验时，只要把所考察的每一个因

9、子任意地对应于正交表的一列(一个因子对应一列，不能让两个因子对应同一列)，然后把每列的数字"翻译”成所对应因子的水平。这样，每一行的各水平组合就构成了一个试验条件(不考虑没安排因子的列)。对于例1,因子A、RC都是三水平的，试验次数要不少于3X(3-1)+1=7(次)可考虑选用L9(34)。因子A、B、C可任意地对应于L9(34)的某三列，例如AB、C分别放在1、2、3歹I，然后试验按行进行，顺序不限，每一行中各因素的水平组合就是每一次的试验条件，从上到下就是这个正交试验的方案，见表2。这个试验方案的几何解释正好是图2。表2因子安排试差方案行号A12C34水平组合试验条件温度（D时间

10、份）加碱量恒111111gc1如905212222a世炉口SO120631333口33015014212344孙G打%6522315AjBjCj85120162312A乱685150513131总3aLe390%183213S9012053321g如1506三个3水平的因子，做全面试验需要33=27次试验，现用L9（34）来设计试验方案，只要做9次，工作量减少了2/3,而在一定意义上代表了27次试验.。再看一个用L9（34）安排四个3水平因子的例子。例2某矿物气体还原试验中，要考虑还原时间（A）、还原温度（B）、还原气体比例（D）、气体流速（C）这四个因子对全铁合量X越高越好）、金属化率Y（越

11、高超好）、二氧化钛含量Z（越低越好）这三项指标的影响。希望通过试验找出主要影响因素，确定最适工艺条件。首先根据专业知以确定各因子的水平：时间：A1=3（小时）,A2=4（小时）,A3=5（小时）温度：B1=1000（C）,B2=1100（C）,B3=1200（C）流速：Cl=600（毫升/分），C2=400（毫升/分），C3=800（毫升/分）CO:H2D1=1:2,D2=2:1,D3=1:1这是四因子3水平的多指标（X、Y、Z）问题，如果做全面试验需34=81次试验,而用L9（34）来做只要9次。具体安排如表3。同全面试验比较，工作量少了8/9。由于缩短了试验周期，可以提高试验精度，时间越长

12、误差于扰越大。并且对于多指标问题，采用简单对比法，往往顾此失彼，最适工艺条件很难找；而应用正交表来设计试验时可对各指标通盘考虑，结论明确可靠。表M试朝霎试验号水平组合1试范J条件时间«w）温度（七）流量管升,分）COHj1AMCDi310CO6。口1；22A此CQ：311004002=13A1B3CQ331200S001：1441000400：15AiB正必411008001：1641200mZ11直3B1CQ?51000800久18A3B2C1D；51100600h19A,B§CQ512CQ4卯1；24 .试验数据的直观分析正交表的另一个好处是简化了试验数据的计算分折。还

13、是以例1为例来说明按照表2的试验方案进行试验，测得9个转化率数据，见表4。表4转正率试验数据与计算分析因子试验号湿度时间加减里试验结果水平1234转化率（%）11(80T?)吵分）一4浅）13121网口2(120分)2(6%)25431C80C)XI50分)7%)3能42(856)1(90分)式6%)3535WC)2(120分)3(7灼1496跳。）箕分）1海）24273(9CTC)1（卯分）中枪25783(901C)3(120分)10%)36293CP01C)3(15口分)2(6%)164I123141135144II144165171153III183144144153用4147451=4

14、50485557叼634S43R如312S61B1142驾18通过9次试验，我们可以得两类收获。第一类收获是拿到手的结果。第9号试验的转化率为64,在所做过的试验中最好，可取用之。因为通过L9(34)已经把试验条件均衡地打散到不同的部位，代表性是好的。假如没有漏掉另外的重要因素，选用的水平变化范围也合适的话，那么，这9次试验中最好的结果在全体可能的结果中也应该是相当好的了，所以不要轻易放过。第二类收获是认识和展望。9次试验在全体可能的条件中(远不止33=27个组合，在试验范围内还可以取更多的水平组合)只是一小部分，所以还可能扩大。精益求精。寻求更好的条件。利用正交表的计算分折，分辨出主次因素，

15、预测更好的水平组合，为进一步的试验提供有份量的依据。其中I、H、m分别为各对应列(因子)上1、2、3水平效应的估计值，其计算式是：Ii(Hi,IHi)=第i列上对应水平1(2,3)的数据和K1为1水平数据的综合平均=1/水平1的重复次数Si为变动平方和=例1的转化率试验数据与计算分析见表4。先考虑温度对转比率的影响。但单个拿出不同温度的数据是不能比较的，因为造成数据差异的原因除温度外还有其他因素。但从整体上看，80C时三种反应时间和三种用碱量全遇到了，86c时、90c时也是如此。这样，对于每种温度下的三个数据的综合数来说，反应时间与加碱量处于完全平等状态，这时温度就具有可比性。所以算得三个温度

16、下三次试验的转化率之和：80C：IA=xl+x2+x3=31+54+38=123;85C:IIA=x4+x5+x6=53+49+42=144;90C：mA=x7+x8+x9=57+62+64=183。分别填在A列下的I、H、田三行。再分别除以3,表示80C、85C、90c时综合平均意义下的转化率，填入下三行Kl、K2、K3oR行称为极差，表明因子对结果的影响幅度。同样地，为了比较反应时间；用碱量对转化率的影响，也先算出同一水平下的数据和IB、HRmB,Ic、Hc、mc,再计算其平均值和极差。都填入表4中；由此分别得出结论：温度越高转化率越好，以90c为最好，但可以进一步探索温度更好的情况。反应

17、时间以120分转化率最高。用碱量以6%转化率最高。所以最适水平是A3B2C25.正交试验的方差分析(一)假设检验在数理统计中假设检验的思想方法是：提出一个假设，把它与数据进行对照，判断是否舍弃它。其判断步骤如下：(1)设假设H正确，可导出一个理论结论，设此结论为R。；(2)再根据试验得出一个试验结论，与理论结论相对应，设为R1;比较R。与Rl,若R。与Rl没有大的差异，则没有理由怀疑H。，从而判定为："不舍弃K"(采用Ho);若R。与R1有较大差异，则可以怀疑HL,此时判定为："舍弃H"。但是，R1/R。比l大多少才能舍弃H。呢？为确定这个量的界限，需要

18、利用数理统计中关于F分布的理论。若yl服从自由度为61的分布，y2服从自由度为62的分布，并且yl、y2相互独立，则（y1/（I）1）/（y2/62）服从自由度为（小1,小2）的F分布。F分布是连续分布，分布模数是两个自由度（61,62）。称（M为分子自由度，称62为分母自由度。在自由度为（61,62）的F分布中，某点右侧面积为p,也就是F比此值大的概率为p,把这个值写为（p）。若检验的显著性水平（或危险率）给定为a时，则可以把（a）作为临界值来检验假设。这里，Se/（r2服从自由度为de,的分布；当H。成立,22=0时，SA/（72也服从自由度为小A的2分布；又SA与Se相互成立，所以（SA

19、/（小A（r2）/Se/（6e62）=VA/Ve服从自由度为（小A,6e）的F分布。这就是假定H。正确时的理论结论R。而试验结论Rl要与理论结论R相比较。由给定的显著性水平，通常是a=0.05;分子自由度r=A=a-l,分母自由度62=小e=a（n-1）；查F分布表得出（a）。所以H。：al=a2=aa=0（crA2=0）的检验是：（显著性水平a）FA=VA/Ve>（a）舍弃H。FA=VA/Vec（a）不舍弃H。通常，（a）一股性地表示成Fa（小A,小B）。假设因子A对试验结果的影响不显著，那么A的两个水平的效应该表现为相等或相近，即假设H。：a1=a2=0。如果因子A显著，则舍弃假设。

20、为了判断因子A是否显著，首先要计算比值显然，这个比值越大，因子A对指标的影响越显著；反之，因子A就不显著。在给定置信度a后，如a=0.05,查F分布表，自由度（|）A是因子A的，自由度小e是误差的，其临界值Fa（小A,小e）,如果FA>Fa（小A,小e）就舍弃假设，可以认为因子A是显著的；如果FA<Fa（|）A,（|）e）就没有理由否定假设，而只能认为因子A是不显著的。因为按照F分布表的物理念义，F值小于Fa（小A,6e）的概率是95%,即有95%勺机会出现小于Fa（小A,6e）的F值，既然出现了这种情况，就有了95%的把握，所以就没有理由否定假设，只能接受假设，认为因子A不显著。

21、另一方面，F值大于Fa（小A,6e）的概率是5%,也就是只有5%的机会出现大于Fa（小A,小e）的F值，这是小概率事件，如果小概率事件居然发生了，则可认为情况异常，假设不可信，必须否定假设，因子A是显著的。对其他因子的显著性检验完全类似。（二）方差分析表由总平方和与各因素平方和即可求得误差平方和，亦称剩余平方和。是总平方和减各因素平方和所得。如正交表有一空列，则该列的平方和就量误差平方和。但在正交表饱和试验的情况下，即所有各列全部排满时，误差平方和一般用各因素平方和中几个最小的平方和之和来代替，同时，这几个因素不再作进一步的分析。自由度：小T=试验次数一1（|）AB=水平数一1小AXB=（|）

22、AX小Bee=jT-（J）A-（J）B-（J）D表5化工产品试骗方差分析表为发来覆孚方利自由度F鱼显著性1518234.3*时间114263加神?弘213、口耳13®132补充内容一、什么是正交试验设计正交试验设计（Orthogonalexperimentaldesign）是研究多因素多水平的又一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了均匀分散，齐整可比”的特点，正交试验设计是分析因式设计的主要方法。是一种高效率、快速、经济的实验设计方法。日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格，称为正交表。例如作一个三因素三水平

23、的实验，按全面实验要求，须进行3A3=27种组合的实验，且尚未考虑每一组合的重复数。若按L9（3）正交表安排实验，只需作9次，按L18（3）正交表进行18次实验，显然大大减少了工作量。因而正交实验设计在很多领域的研究中已经得到广泛应用。正交表是一整套规则的设计表格，用L为正交表的代号，n为试验的次数，t为水平数，c为列数，也就是可能安排最多的因素个数。例如L9（3M）它表示需作9次实验，最多可观察4个因素，每个因素均为3水平。一个正交表中也可以各列的水平数不相等，我们称它为混合型正交表，如L8（4X2）此表的5列中，有1列为4水平，4列为2水平。二、正交试验设计表正交试验设计表正交试验因素水平

24、表正交试验设计方案及试验结果极差分析表（或指标与因素关系图）方差分析表（简单分析时可无）正交表的性质（1）每一列中，不同的数字出现的次数相等。例如在两水平正交表中，任何一列都有数码“1与“2；且任何一列中它们出现的次数是相等的；如在三水平正交表中，任何一列都有“1：”27”3；且在任一列的出现数均相等。（2）任意两列中数字的排列方式齐全而且均衡。例如在两水平正交表中，任何两列（同一横行内）有序对子共有4种：（1,1）、（1,2）、（2,1）、（2,2）。每种对数出现次数相等。在三水平情况下，任何两列（同一横行内）有序对共有9种，1.1、1.2、1.3、2.1、2.2、2.3、3.1、3.2、3

25、.3,且每对出现数也均相等。以上两点充分的体现了正交表的两大优越性，即均匀分散性，整齐可比通俗的说，每个因素的每个水平与另一个因素各水平各碰一次，这就是正交性。正交表的获得有专门的算法，对应用者来说，不必深究。正交试验设计的安排正交试验设计的关键在于试验因素的安排。通常，在不考虑交互作用的情况下，可以自由的将各个因素安排在正交表的各列，只要不在同一列安排两个因素即可（否则会出现混杂）。但是当要考虑交互作用时，就会受到一定的限制，如果任意安排，将会导致交互效应与其它效应混杂的情况。因素所在列是随意的，但是一旦安排完成，试验方案即确定，之后的试验以及后续分析将根据这一安排进行，不能再改变。对于部分

26、表，如L18（2*3人7）则没有交互作用列，如果需要考虑交互作用需要选择其它的正交表。正交试验设计的极差分析在完成试验收集完数据后，将要进行的是极差分析（也称方差分析）。极差分析就是在考虑A因素时，认为其它因素对结果的影响是均衡的，从而认为，A因素各水平的差异是由于A因素本身引起的。用极差法分析正交试验结果应引出以下几个结论：在试验范围内，各列对试验指标的影响从大到小的排队。某列的极差最大，表示该列的数值在试验范围内变化时，使试验指标数值的变化最大。所以各列对试验指标的影响从大到小的排队，就是各列极差D的数值从大到小的排队。试验指标随各因素的变化趋势。使试验指标最好的适宜的操作条件（适宜的因素

27、水平搭配）。对所得结论和进一步研究方向的讨论。较优条件选择各因素的好水平加在一起，是否就是较优试验条件呢？理论上，如果各因素都不受其它因素的水平变动影响的，那么，把各因素的优水平简单地组合起来就是较好试验条件。但是，实际上选取较好生产条件时，还要考虑因素的主次，以便在同样满足指标要求的情况下，对于一些比较次要的因素按照优质、高产、低消耗的原则选取水平，得到更为结合试验实际要求的较好生产条件。以上介绍如何分析各因素水平的变动对指标的影响。讨论A因素时，不管其它因素处在什么水平，只从A的极差就可判断它所起作用的大小。对其它因素也作同样的分析，在此基础上选取谙因素的较优水平。实践中发现，有时不仅因素

28、的水平变化对指标有影响，而且，有些因素间各水平的联合指配对指标也产生影响，这种联合搭配作用称为交互作用。而交互作用应该在试验设计时考虑到。三、正交试验分析方法直接对比法直接对比法就是对试验结果进行简单的直接对比。直接对比法虽然对试验结果给出了一定的说明，但是这个说明是定性的，而且不能肯定地告诉我们最佳的成分组合。显然这种分析方法虽然简单，但是不能令人满意。直观分析法直观分析法是通过对每一因素的平均极差来分析问题。所谓极差就是平均效果中最大值和最小值的差。有了极差，就可以找到影响指标的主要因素，并可以帮助我们找到最佳因素水平组合。四、正交试验设计的基本思想考虑进行一个三因素、每个因素有三个水平的

29、试验。如果作全面试验，需作3A3=27次。图:正交试验设计示意图若从27次试验中选取一部分试验，常将A和B分别固定在A1和B1水平上，与C的三个水平进行搭配，A1B1C1,A1B1C2,A1B1C3。作完这3次试验后，若A1B1C3最优，则取定C3这个水平，让A1和C3固定，再分别与B因素的三个水平搭配，A1B1C3,A1B2c3,A1B3c3。这3次试验作完以后，若A1B2c3最优，取定B2,C3这两个水平，再作两次试验A2B2c3,A3B2c3,然后与一起比较，若A3B2C3最优，则可断言A3B2C3是我们欲选取的最佳水平组合。这样仅作了8次试验就选出了最佳水平组合。我们发现，这些试验结果

30、都分布在立方体的一角，代表性较差，所以按上述方法选出的试验水平组合并不是真正的最佳组合。如果进行正交试验设计，利用正交表安排试验，对于三因素三水平的试验来说，需要作9次试验，用“谯示，标在图中。如果每个平面都表示一个水平，共有九个平面，可以看到每个平面上都有三个“熬，立方体的每条直线上都有一个“靖，并且这些“点是均衡地分布着，因此这9次试验的代表性很强，能较全面地反映出全面试验的结果，这就是正交实验设计所特有的均衡分散性。我们正是利用这一特性来合理的设计和安排试验，以便通过尽可能少的试验次数，找出最佳水平组合。五、正交试验设计的过程1)确定试验因素及水平数；2)选用合适的正交表；3)列出试验方

31、案及试验结果；4)对正交试验设计结果进行分析，包括极差分析和方差分析；5)确定最优或较优因素水平组合。正交试验设计法与遗传算法的联系2(1)正交试验设计法是遗传算法的一种特例，即正交试验设计法是一种初始种群固定的、只使用定向变异算子的、只进化一代的遗传算法。(2)遗传算法的步骤比正交试验设计法复杂，所需的试验次数也要多于正交试验设计法的试验次数，但它产生的解要优于正交试验设计法产生的解。(3)遗传算法的隐并行性使得它在处理交互作用项时，效率比正交试验设计法要(Wj。(4)正交试验设计法可解决一般遗传算法中的最小欺骗问题。六、正交试验设计的案例分析案例：水稻播种机穴盘育秧播种装置1.水稻播种机穴

32、盘育秧播种装置的试验设计随着栽培技术的不断更新，高效、节本、高产的抛秧栽培法获得了迅速发展和推广。为了改善原有播种装置中窝眼辐轮结构，我们研制成功了穴盘育秧播种装置，它不仅解决了手工操作进行育秧培育的劳动强度大，工作效率低等问题，而且能大幅度地提高播种量的稳定性和播种的均匀性，使水稻播种机械更趋实用与完善。（1）试验目的考虑影响播种性能的主要因素对水稻播种机穴盘育秧播种装置播种性能的影响程度，以达到优化设计参数。（2）试验条件种子品种：杂交稻（协优46号）种子状况：经过脱芒、浸种、催芽露白、去杂质秧盘规格：600m丽340mm,561穴种子千粒重：26.9g试验盘数：100盘秧盘运行速度与排种

33、胶带线速度严格一致。（3）试验因素A.可变因素选用三个可变因素：生产率（盘/小时）、播种量（粒/穴）、投种高度（mm）。B.可变的水平数每个因素分别取三个水平数C.实验因素与水平为了研究生产率、播种量及投种高度对播种性能的影响，特安排了三因素三水平的正交试验，试验因素与水平见下表所示。试验因素与水平水平因素*生产率八盘/小时）因素R瑞种量/（做/穴投和而度，nun1300小门502360中1003400)J502 .正交试验方案与试验结果分析（1）正交试验方案与试验结果选用L9（34）正交表进行试验设计，试验方案与试验结果见下表所示。其数据采集方法为：在每种工况（每个试验号）条件下进行随机抽样5盘测定，测定播种合格率时，每盘随机连片抽样100穴。最后，把5次测定的各项数据的平均值记入试验结果。正交