北京交通大学信号与系统大作业

1、信号与系统大作业学院：电气工程学院班级：电气0909班姓名：m学号：09292024指导教师：邱瑞昌老师09292024熊飞用MATLAB验证时域抽样定理目的：通过MATLA褊程实现对时域抽样定理的验证，加深抽样定理的理解。同时训练应用计算机分析问题的能力。任务:连续信号f(t)=cos(8*pi*t)+2*sin(40*pi*t)+cos(24*pi*t),经过理想抽样后得到抽样信号fs(t),通过理想低通滤波器后重构信号f(t)。可得信号的傅里叶变换为:X(t),f，二卜(w8二)(w-8二)2卜(w40二)-(w-40二)二卜(w24二)(w-24二)所以X(t)的最高频率是40n,所以

2、Niquist采样间隔为Tn=0.025S,理想低通滤波器为了能够完整恢复波形，选择Wc=1.1Wsam即可。程序设计：主程序：wm=40*pi;确定信号最大角频率wc=1.1*wm;确定低通滤波器的通带宽度Ts=0.02;确定采样时间问隔n=-200:200;nTs=n*Ts;制造周期采样脉冲序列fs=(cos(8*pi*nTs)+2*sin(40*pi*nTs)+cos(24*pi*nTs);进行信号采样t=-0.3:0.0001:0.3;ft=fs*Ts*wc/pi*sinc(wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t);

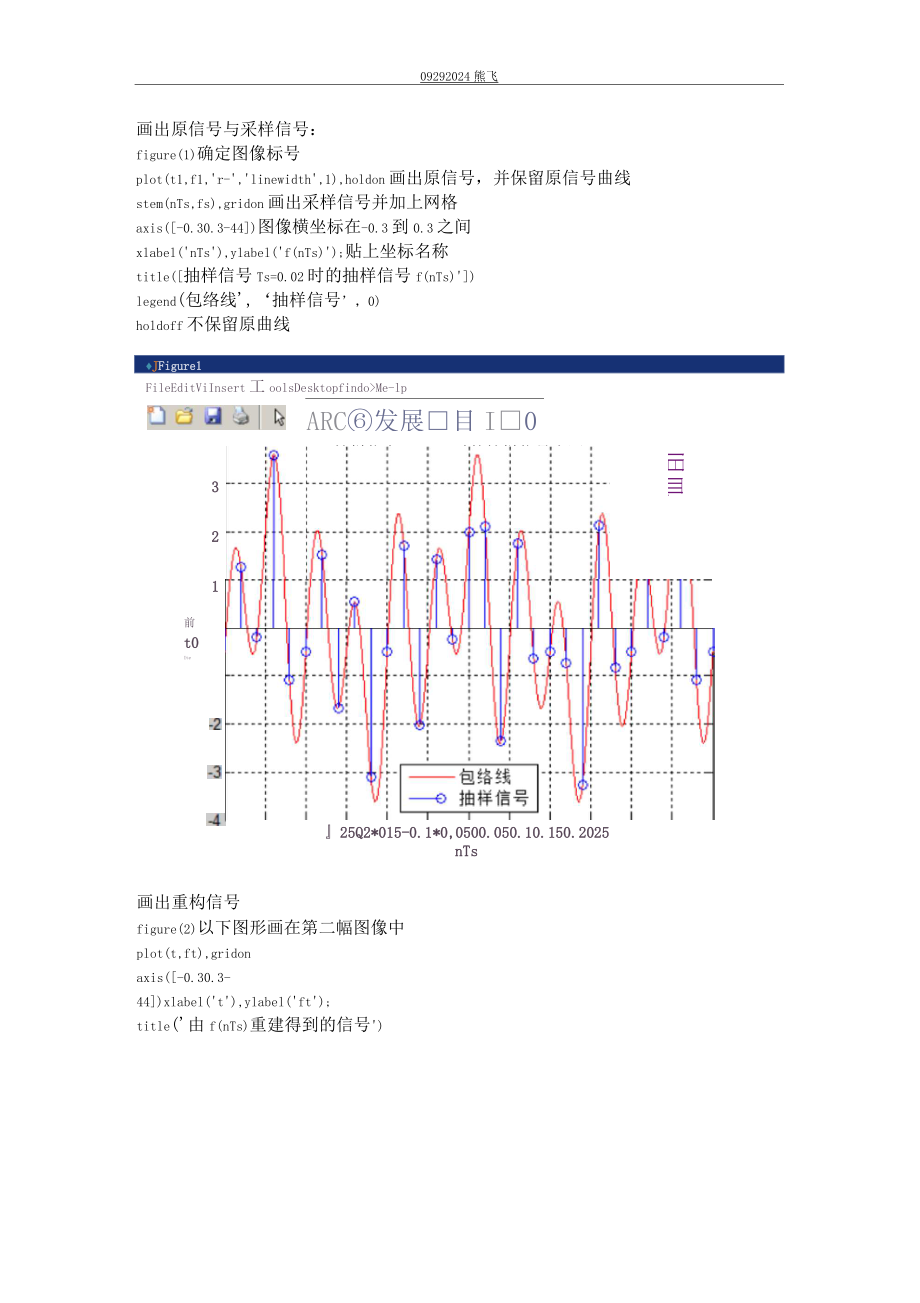
3、确定重构信号的时间范围。t1=-0.3:0.0001:0.3;f1=cos(8*pi*t1)+2*sin(40*pi*t1)+cos(24*pi*t1);制造原连续信号09292024熊飞画出原信号与采样信号：figure(1)确定图像标号plot(t1,f1,'r-','linewidth',1),holdon画出原信号，并保留原信号曲线stem(nTs,fs),gridon画出采样信号并加上网格axis(-0.30.3-44)图像横坐标在-0.3到0.3之间xlabel('nTs'),ylabel('f(nTs)');贴上坐标

4、名称title(抽样信号Ts=0.02时的抽样信号f(nTs)')legend(包络线',抽样信号，0)holdoff不保留原曲线JFigure1FileEditViInsert工oolsDesktopfindo>Me-lpARC发展目I0抽样信言Ts=O02时的抽样信号也网321前t0Ite-1旧皿illi25Q2*015-0.1*0,0500.050.10.150.2025nTs画出重构信号figure(2)以下图形画在第二幅图像中plot(t,ft),gridonaxis(-0.30.3-44)xlabel('t'),ylabel('ft&#

5、39;);title('由f(nTs)重建得到的信号')JFiar世209292024熊飞-ln|x|FileEditVie«InsertTenolsDesktopthndewHelp4咫组目国由好同信号重建得到的信号4321h0-1"425-0.216闻140500.050.10,1502025t画出误差波形error=abs(ft-f1);定义误差量Rgure(3);画在第三幅图像中plot(t,error),gridonaxis(-0.30.3-0.14)xlabel('t'),ylabel('error(t)');ti

6、tle('重建新号与原信号的绝对误差')09292024熊飞当采样信号变为0.03秒时，同样可得三幅图片:09292024熊飞09292024熊飞实验分析与总结我们可以看出当采样周期小于Niquist间隔时能够实现信号采样后频谱的不混叠采样，这样一来，只要低通滤波器的带通宽度合适即可实现原信号的不失真重构。但是若采样周期大于Niquist间隔，就会发生信号采样后频谱的混叠情况,这时，即使用合适的低通滤波器也不会将原信号重构出来。同样地，若低通滤波器的频带宽度选择不好也不能实现信号的不失真重构。为此我做出如下两图：在采样周期为0.02S时，图一：低通滤波器的通带宽度为Wc=2Wm图二：低通滤波器的通带宽度为Wc=0.9Wm可以看出，低通滤波器要保证在其通带中只能够有一个完整的不混叠的原始信号的频谱，否则就将失真。而且该例子也未将低通滤波器的延迟考虑进来，默认延迟为零。09292024熊飞J012(1FilEditLn*rtTgolfDwfktapH,lpUj*AQ咫相注，0EnO重建信号与原信号的绝对误差Q26-02-0.15Q1Q0500.0501015。一2025fileEditViInsertto