3刚体力学习题详解

1、习题三一、选择题1. 一根长为I、质量为M的匀质棒自由悬挂于通过其上端的光滑水平轴上。现有一质量 为m的子弹以水平速度 V0射向棒的中心，并以 V0/2的水平速度穿出棒，此后棒的最大偏 转角恰为90，那么V0的大小为答案:解:(A) 4M gl(B):g;(C) 2M gF ；m(D)。3m2VdJ1 1 J11j 22MgJ ,1l2J11Ml2l/22V0lVo/2l/2Vo1 12JlMV0/2m1 -J2MglJ112JMgl ,2 2专Mglml2 24応4 产4 】MI23Mgl ,316Mgl ,2V0216 M牙gl，所以3 mvo4Mm 3gi2.圆柱体以24 kg m作用下

2、，10s80rad/s的角速度绕其轴线转动，它对该轴的转动惯量为内其角速度降为40rad/s。圆柱体损失的动能和所受力矩的大小为。在恒力矩答案:解：(A) 80J, 80 N m ;D(B) 800J, 40 N(C) 4000J, 32N m ; (D) 9600J, 16N m。0 80 ,40 ,10 ,1J 22M恒定，匀变速，所以有EkEk11J(2)(64001600)9600(J)16N103. 一个转动惯量为J的圆盘绕一固定轴转动，初角速度为 °。设它所受阻力矩与转动角速度成正比M k k为正常数。1它的角速度从 0变为0/2所需时间是(A)J/2 ;(B) J/k

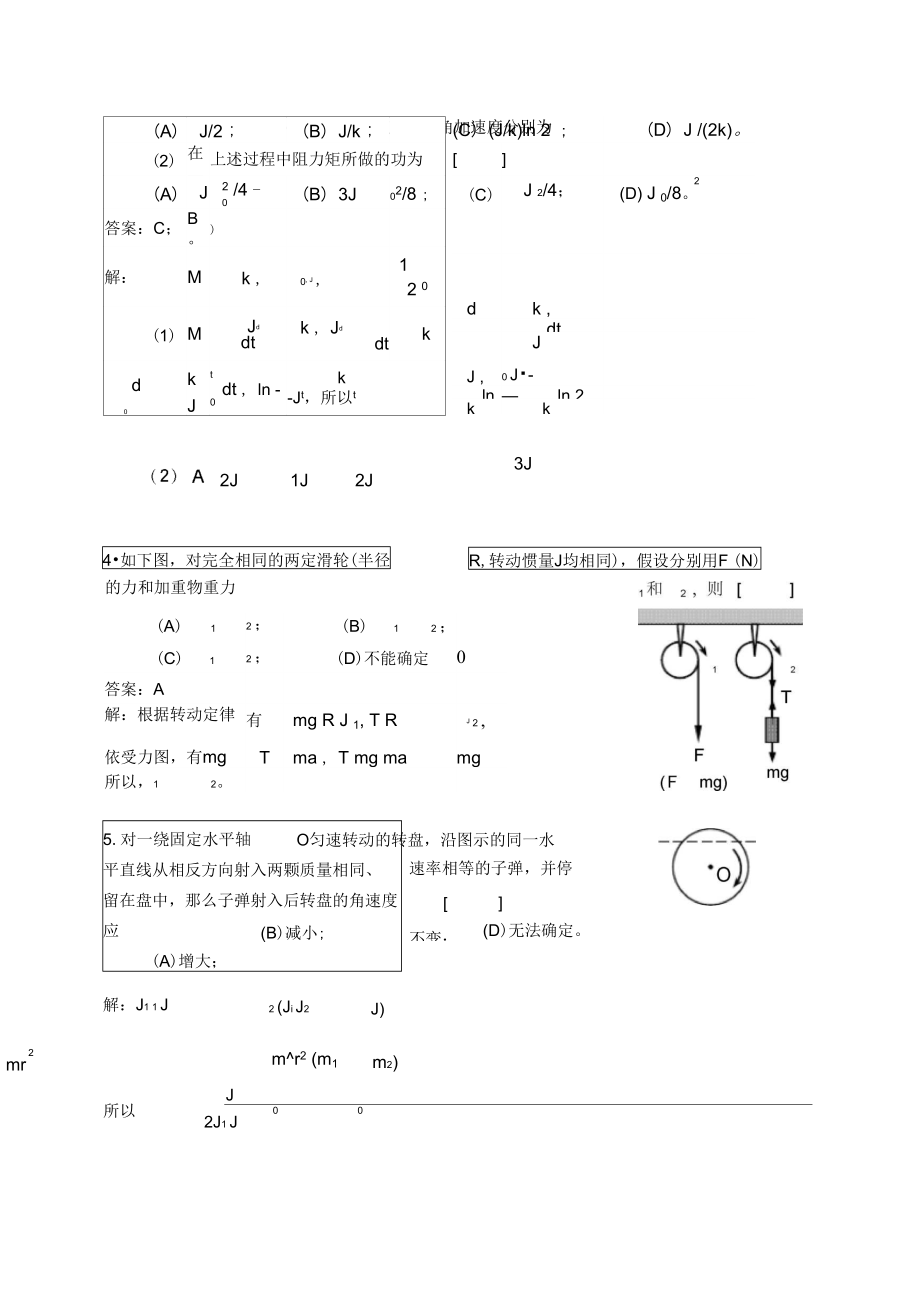
3、;(2)在上述过程中阻力矩所做的功为(A)J2 /4 -0(B) 3J02/8 ;答案：C；B。)解：Mk ,0, J ,12 0(1)MJddtk , Jddtkd0kJtdt , ln -0k-Jt，所以t(C) (J/k)ln 2 ；(D) J /(2k)。(C)J 2/4；2(D) J 0/8。dk ,dtJJ ,0 J-ln -ln 2kk2J1J2J3J4如下图，对完全相同的两定滑轮(半径R,转动惯量J均相同)，假设分别用F (N)P mg F (N)时，所产生的角加速度分别为(A)12 ；(B)12 ；(C)12 ；(D)不能确定0答案：A解：根据转动定律，有mg R J 1,

4、T RJ 2 ,依受力图，有mgTma , T mg mamg所以，12。的力和加重物重力5.对一绕固定水平轴平直线从相反方向射入两颗质量相同、 留在盘中，那么子弹射入后转盘的角速度应(A)增大；答案：BO匀速转动的转盘，沿图示的同一水 速率相等的子弹，并停不变；(B)减小;(D)无法确定。解：J1 1 J2 (Ji J2J)2mrmr2 (m1m2)，所以J002J1 J二、填空题1半径为r 1.5m的飞轮，初角速度 o=1Orad/s，角加速度5rad/s2，假设初始时刻角位移为零，那么在t 时角位移再次为零， 而此时边缘上点的线速度为v 。答案：4s ；15m/s。解： r 1.5m，0

5、=10rad/s，25rad/s ，00。1 因con st，为匀变速，所以有00t - t2。21 2 2 10令 0,即0 tt 0得，由此得 t一04s25t 10 5 410，所以r 15m/s2. 一根质量为 m、长度为L的匀质细直棒，平放在水平桌面上。假设它与桌面间的滑动 摩擦系数为，在t 0时，使该棒绕过其一端的竖直轴在水平桌面上旋转，其初始角速度为0,那么棒停止转动所需时间为 答案：t2 °L3"g解：df dmgdrg所以dt3dt2Ld3 g0dt ,dt3 gdt，两边积分得：03 gt ,2L00 2L2L又，M J J J1mL2dmg，所以t2

6、0L3 gr V V-mm 1 2mgdM r df , dM rdfgrdr ,MdMg LLL22L3. 在自由旋转的水平圆盘上，站一质量为m的人。圆盘半径为 R,转动惯量为J,角速度为。如果这人由盘边走到盘心，那么角速度的变化=;系统动能的变化 Ek =。2 2 答案：皿；1mR2 2迟1。J 2J解：应用角动量守恒定律JmR2J解得mR2J，角速度的变化mR2系统动能的变化1 1Ek 2 J 2 A mR22，即Ek21 m2 2 zmR八-mR2 2(1)2 J4.如下图，转台绕中心竖直轴以角速度0作匀速转动，转台对该轴的转动惯量J 5 10 5kg m2。现有砂粒以1g/s的流量落

7、到转台，并粘在台面形成一半径r 0.1m的圆。那么使转台角速度变为o/2所花的时间为。I宀答案：5s解：由角动量守恒定律(Jmr2)2得 m所以由于10 3 kg/s5 10 5t 1 10 3 r2 1 10 3 0.12 1 10 35s5.如下图，一轻绳跨过两个质量均为 m、半径均为 分别系着质量分别为 m和2m的重物，不计滑轮转轴的 摩擦。将系统由静止释放，且绳与两滑轮间均无相对滑 动，那么两滑轮之间绳的张力为答案：T 11 mg8omgma(1)解：列出方程组T2m2gm2a入T)RJ1 1(TT2)R2J2 2其中，1 RJ1 2MR2,2aJ21m2r22 2由1、2两式得:T1

8、 g(gT2 m2(ga)a)可先求出a,解得m12(mi mQg2(m1 m2) (M1 M2)4m1 m2 m1(M1 M2)2(m1 _m2) (M1 _Mj § ，T24mim2 m2(M1 M 2)4m1m2 m1M2 m2M12(m1 m2) (M1 M2)g，T_m,) (M1 _g将 m1 2m,三.计算题1 在半径为擦地绕过盘中心的竖直轴转动。当这人沿着与圆盘同心，半径为 于圆盘走一周时，问圆盘和人相对于地面转动的角度各为多少？24 mR2R1、质量为M的静止水平圆盘上，站一静止的质量为m的人。R2 < R1圆盘可无摩的圆周相对答案：12mkMR2 '

9、或4-( 2)MR；/(mR：)2mR22 MR122 ?MR；或 222mR2/(MR；) 1解：设人相对圆盘的角速度为圆盘相对地面的角速度为那么人相对地面的角速度为应用角动量守恒定律mR21MR12M 0 得，mR2解得mR222m&2mR2 2mr12圆盘相对地面转过的角度为2 22mR,MR1Mdt2mR222mR MR2dt2mR,22mR MR22 MR2/(mR2)人相对地面转过的角度为mmdt 22 MR；2mR； MR22mR?/(MR12) 111m M1 M 2 m, R R2 代入，得：T mg82. 如下图，物体1和2的质量分别为 m1与m2，滑轮的转动惯量为

10、 J,半径为r。1如物体2与桌面间的摩擦系数为，求系统的加速度 a及绳中的张力和T2；2如物体2与桌面间为光滑接触，求系统的加速度a及绳中的张力T1和T2。设绳子与滑轮间无相对滑动，滑轮与转轴无摩擦。答案：太长，略。解: 1用隔离体法，分别画出三个物体的受力图。 对物体1，在竖直方向应用牛顿运动定律T1mea)对物体2，在水平方向和竖直方向分别应用牛顿运动定律T2 Nm2a， N mg 0对滑轮，应用转动定律T2r T,rJ ，并利用关系a rNTa m1 m2 g Tm2m.Jr1m n ； 丁a g， T1jmg，T2Jmm?2rr(2)0 时Jm22rm2ga m g ； Taj g ；

11、 T1m)1m?2rj mg ； T2m)1m)22rm1_Jr3. 匀质细杆，质量为 0.5Kg，长为0.4m，可绕杆一端的水平轴旋转。假设将此杆放在水平 位置，然后从静止释放，试求杆转动到铅直位置时的动能和角速度。答案：10.98J ； 28.57rad/s。1 1解：根据机械能守恒定律，有：mg J2 2别为：。杆转动到铅直位置时的动能和角速度分EkJ 2 mg-0.5 9.8 0.2 0.98J ；2 2mglmgl8.57rad/s由以上各式，解得K4如下图，滑轮的转动惯量J =0.5kg m2,半径r =30cm，弹簧的劲度系数 k =2.0N/m ,重物的质量m =2.0kg。当

12、此滑轮一一重物系统从静止开始启动，开始时弹簧没有伸长。滑轮与绳子间无相对滑动，其它局部摩擦忽略不计。问物体能 沿斜面下滑多远？当物体沿斜面下滑 1.00m时，它的速率有多 大？答案：1 11.8m ； 2 1.7m/s。解：以启动前的位置为各势能的零点，启动前后应用机械能守恒定律 kx22 1 2mv2mgxs in 3700(1)0时,2 2° 9.8 sin37 11.8m(2)1 -m2Ikx22.0 9.8 sin37 丄 2 1222mg sin371 2.0 1 °5222 (0.3)21 J2 r21.7m/s1.00kg的匀质木棒，可绕水平轴O在竖直平面内转动，开始点射入棒中，A、O 棒的最大偏转角。5.长时棒自然竖直悬垂，现有质量m 8g的子弹以v 200m/s的速率从A点的距离为3l/4，如下图。