固体物理习题解答ppt课件

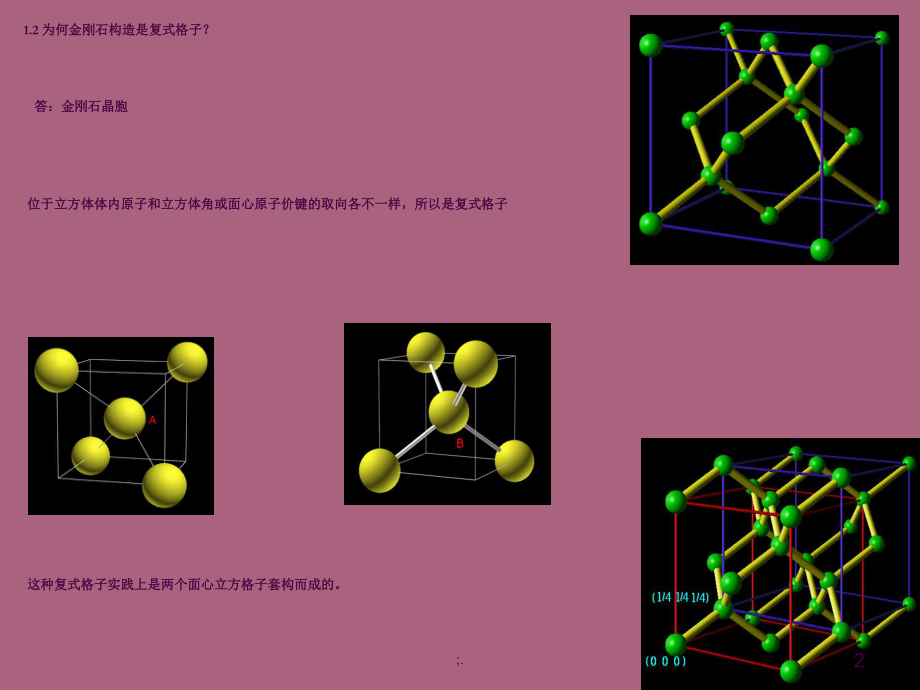
1、1.1 何谓布喇菲格子？试画出何谓布喇菲格子？试画出NaCl晶体的结点所构成的布喇菲格子。晶体的结点所构成的布喇菲格子。答：所谓布喇菲格子是指晶体由完全一样的原子组成，原子与晶格的格点相重合，而且每个格点周围的情况都一样。答：所谓布喇菲格子是指晶体由完全一样的原子组成，原子与晶格的格点相重合，而且每个格点周围的情况都一样。Bravais格格子子氯化钠构造：面心立方氯化钠构造：面心立方Na+布氏格子和面心立方布氏格子和面心立方Cl-的布氏格子套构而成的复式格子。的布氏格子套构而成的复式格子。1;.1.2 为何金刚石构造是复式格子？为何金刚石构造是复式格子？答：金刚石晶胞答：金刚石晶胞位于立方体体

2、内原子和立方体角或面心原子价键的取向各不一样，所以是复式格子位于立方体体内原子和立方体角或面心原子价键的取向各不一样，所以是复式格子这种复式格子实践上是两个面心立方格子套构而成的。这种复式格子实践上是两个面心立方格子套构而成的。2;.1.3 对于六角密堆积构造，试证明：对于六角密堆积构造，试证明： 。1/28( )1.6333ca底面原子及与体心原子之间均严密接触底面原子及与体心原子之间均严密接触222323caa1/281.6333ca那么红线的长度为那么红线的长度为33ya2222cyac/2aac/2aa假设假设 ，那么可以为是由原子密排面所组成，但这些平面之间是疏松堆积的。，那么可以为

3、是由原子密排面所组成，但这些平面之间是疏松堆积的。1.633ca3;.1.4 金属金属Na在在273K因马氏体相变从体心立方转变为六角密堆积构造，假定相变时金属的密度维持不变，知立方相的晶格常数因马氏体相变从体心立方转变为六角密堆积构造，假定相变时金属的密度维持不变，知立方相的晶格常数ac =0.423nm，设六角密堆积构造相的设六角密堆积构造相的c/a维持理想值，试求其晶格常数。维持理想值，试求其晶格常数。 解：体心立方每个晶胞包含解：体心立方每个晶胞包含2个原子，一个原子所占的体积为个原子，一个原子所占的体积为单位体积内原子数即密度为单位体积内原子数即密度为23ccaV 六角密堆积每个晶胞

4、包含六角密堆积每个晶胞包含6个原子，一个原子所占的体积为个原子，一个原子所占的体积为1Vc即：即：32122223843436/323aaacacaaVs由于密度不变，所以由于密度不变，所以scVV1133222/aac16/20.377caanmnmacs615. 0633. 14;.1.5 如将等体积的刚球分别排成简立方、体心立方、面心立方、六角密积以及金刚石构造，设如将等体积的刚球分别排成简立方、体心立方、面心立方、六角密积以及金刚石构造，设x表示刚球体积与总体积之比，试针对不同表示刚球体积与总体积之比，试针对不同的构造求的构造求x 。解：理想晶体是由刚性原子球堆积而成，一个晶胞中刚性原

5、子球占据的体积与晶胞体积的比值称为晶体的致密度，即题中的解：理想晶体是由刚性原子球堆积而成，一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为晶体的致密度，即题中的x设设n为一个晶胞中的刚性原子球数，为一个晶胞中的刚性原子球数，r表示刚性原子球半径，表示刚性原子球半径，V表示晶胞体积，那么致密度为表示晶胞体积，那么致密度为343nrxV5;.(1) 简单立方简单立方恣意一个原子球有恣意一个原子球有6个最近邻，假设原子以刚性球堆积，那么有个最近邻，假设原子以刚性球堆积，那么有a334( )326axa32 ,ar Va晶胞内包含一个原子，所以有：晶胞内包含一个原子，所以有：恣意一个原子球有恣意一

6、个原子球有8个最近邻，假设原子以刚性球堆积，那么体心原子与处在个最近邻，假设原子以刚性球堆积，那么体心原子与处在8个顶角位个顶角位置处的原子球相切，因此，对角线长度为置处的原子球相切，因此，对角线长度为(2) 体心立方体心立方a34ar晶胞体积为晶胞体积为3Va34ra33432()3348axa晶胞内包含晶胞内包含2个原子，所以有：个原子，所以有：6;.(3) 面心立方面心立方(4) 六角密积六角密积a恣意一个原子球有恣意一个原子球有12个最近邻，假设原子以刚性球堆积，那么面心原子与面角处个最近邻，假设原子以刚性球堆积，那么面心原子与面角处4个原子球个原子球相切，因此，面对角线长度为相切，因

7、此，面对角线长度为24ar晶胞体积为晶胞体积为3Va33424()2346axa晶胞内包含晶胞内包含4个原子，所以有：个原子，所以有：恣意一个原子球有恣意一个原子球有12个最近邻，假设原子以刚性球堆积，那么面心原子与面上其它个最近邻，假设原子以刚性球堆积，那么面心原子与面上其它6个原子个原子球相切，因此有球相切，因此有2ar晶胞体积晶胞体积2213 3(6sin60 )22oVcaca 由第由第1题知题知82433car晶胞内包含晶胞内包含6个原子，所以有：个原子，所以有：3246( )23263 32axca7;.(5) 金刚石构造金刚石构造恣意一个原子球有恣意一个原子球有4个最近邻，假设原

8、子以刚性球堆积，那么空间对角线四分之一处的原子个最近邻，假设原子以刚性球堆积，那么空间对角线四分之一处的原子与三个面上的面心原子球及顶角处原子球相切，因此有与三个面上的面心原子球及顶角处原子球相切，因此有38ar晶胞体积为晶胞体积为3Va33438()33816axa晶胞内包含晶胞内包含8个原子，所以有：个原子，所以有：简立方、体心立方、面心立方、六角密积以及金刚石构造的致密度依次为简立方、体心立方、面心立方、六角密积以及金刚石构造的致密度依次为63826263168;.1.61aai 2aaj 3()2aaijk 基矢为基矢为的晶体为何种构造？的晶体为何种构造？方法方法1：先计算出原胞体积：

9、先计算出原胞体积31231()2Vaaaa 由原胞体积可推断为体心构造由原胞体积可推断为体心构造方法方法2：由知的三个基矢构造三个新的基矢：由知的三个基矢构造三个新的基矢1312323123()2()2()2aaaaijkaaaaijkaaaaaijk 由此可推断为体心构造由此可推断为体心构造9;.1.7、1.8、1.9、1.10、1.12和和1.13见课件见课件1.11 知三斜晶系的晶体中，三个基矢为知三斜晶系的晶体中，三个基矢为 ， 和和 , 现测知该晶体的某一晶面法线与基矢的夹角依次为现测知该晶体的某一晶面法线与基矢的夹角依次为、和和，试求该晶面的面指数，试求该晶面的面指数1a 2a 3

10、a 332211coscoscoshadhadhaddahdahdahcoscoscos332211晶面指数为晶面指数为 dadadacoscoscos321)cos,cos,cos(321sss其中其中 是保证是保证 为互质数的因子为互质数的因子,称为互质因子称为互质因子 321,sss321,hhh解：解：最接近原点的晶面在三个基矢上的截距分别为最接近原点的晶面在三个基矢上的截距分别为312123aaahhh、10;.1.14 如下图，如下图，B、C两点是面心立方晶胞上的两面心，求：两点是面心立方晶胞上的两面心，求： 1ABC面的密勒指数；面的密勒指数； 2AC晶列的指数。晶列的指数。BC

11、Aabc矢量矢量 与矢量与矢量 的叉乘即是的叉乘即是ABC面的法线矢量面的法线矢量BA BC BAOAOB 11()()(2)22abbcabcBCOCOB 211(2)()(3)224aBA BCabcacijk ABC面的密勒指数为面的密勒指数为(131)11(2)2aijk111()()()222cabbca ik11;.2AC晶列的指数晶列的指数BCAabcACOCOA 11()()(2 )22cababa ijk 所以所以AC晶列的晶列指数为晶列的晶列指数为11212;.第二章第二章 习题习题2.1 证明简单六角布喇菲格子的倒格子仍为简单六角布喇菲格子，并给出其倒格子的晶格常数。证明

12、简单六角布喇菲格子的倒格子仍为简单六角布喇菲格子，并给出其倒格子的晶格常数。解：在直角坐标系中，简单六角布喇菲格子的基矢为：解：在直角坐标系中，简单六角布喇菲格子的基矢为：zcayaxaaxaa232321相应的倒格子基矢为：相应的倒格子基矢为：zccazaaaaaabyacayacaaaaabyxacayacxacaaaaab22323223322232221233322232123222232121323211322321321容易看出此倒格子为简单六角布喇菲格子容易看出此倒格子为简单六角布喇菲格子晶格常数为：晶格常数为： 1234 34 3233bbbaac132.2 对正交简单晶格，假

13、设沿三个基矢方向的周期分别为对正交简单晶格，假设沿三个基矢方向的周期分别为a、b和和c的，当入射的，当入射X射线方向沿射线方向沿100方向其反复周期为方向其反复周期为a时，试确定在哪些方向时，试确定在哪些方向上会出现衍射极大？什么样的上会出现衍射极大？什么样的X射线波长才干察看到极大？射线波长才干察看到极大？ zcbybbxabzcaybaxaa222321321解：解：zchybhxahbhbhbhGh232133221100kk x恣意倒格矢恣意倒格矢因入射因入射X射线方向沿射线方向沿100方向故有方向故有晶体衍射的布里渊表述晶体衍射的布里渊表述212hhkGG312222hxyzhhhk

14、Gkkkabc假定衍射极大出如今假定衍射极大出如今 方向方向(,)xyzkk kk2222231222212()2hhhhGabc140hkkG31202 ()hhhk xxyzabc3120222()hhhkxyzabc212hhkGG22223312122222222()xyzhhhhhhkkkabcabc3120222xyzhhhkkkkabc22222231122222222xhhhhkaabc2223122221xhhhakhabc152223122221xhhhakhabc3222yzhhkkbc所以衍射极大出如今方向所以衍射极大出如今方向22233122222122(,)xyzh

15、hhhhakk kkxyzhabcbc102xhkka102xhkka2223122221()hhhahabc 为察看到衍射极大要求入射波波长满足为察看到衍射极大要求入射波波长满足1222312022222()hhhhkaabc162.3 证明：体心立方晶格的倒格子是面心立方证明：体心立方晶格的倒格子是面心立方 面心立方晶格的倒格子是体心立方面心立方晶格的倒格子是体心立方 由倒格子定义由倒格子定义2311232aabaaa3121232aaba aa1231232aabaaa体心立方格子原胞基矢体心立方格子原胞基矢)(2),(2),(2321kjiaakjiaakjiaa倒格子基矢倒格子基矢2

16、3112322()()22aaaabijkijka aa22() ()4aijkijk)(2kja同理同理)(22321132kiaaaaaab32()bija可见由可见由 为基矢构成的格子为面心立方格子为基矢构成的格子为面心立方格子 321,bbb17面心立方格面心立方格子原胞基矢子原胞基矢123()/2()/2()/2aa jkaa kiaa ij倒格子基矢倒格子基矢2311232aabaaa)(21kjiab同理同理)(22kjiab)(23kjiab可见由可见由 为基矢构成的格子为体心立方格子为基矢构成的格子为体心立方格子 321,bbb 182.4 证明倒格子原胞体积证明倒格子原胞体

17、积3(2 ) 倒格子基矢倒格子基矢2311232aabaaa3121232aabaaa1231232aaba aa倒格子体积倒格子体积123()bbb 32331123(2 )() () ()aaaaaa 3(2 ) 192.5正格子中晶面指数为正格子中晶面指数为 的晶面和倒格矢正交的晶面和倒格矢正交1 2 3hhh（）hK 1 12233hKh bh bh b 其其中中hK 倒格矢倒格矢 是晶面指数为是晶面指数为 所对应的晶面族的法线所对应的晶面族的法线1 2 3hhh（）意味着意味着1 2 3h h hK 证明证明3113aaCAhh 1 2 31 12233h h hKh bh bh b

18、 1 2 3311 1223313() ()h h haaKCAh bh bh bhh 311 133130aah bh bhh 2ijijab 1 2 30h h hKCB 所以晶面族与和倒格矢正交所以晶面族与和倒格矢正交1 2 3hhh（）1 2 3h h hK 同理可证同理可证20;.2.6 试导出倒格矢的长度与晶面族面间距间的关系试导出倒格矢的长度与晶面族面间距间的关系见课件见课件2.8 试画出周期为的一维布喇菲格子的第一和第二布里渊区。试画出周期为的一维布喇菲格子的第一和第二布里渊区。2.9 试画出边长为的二维正方格子的第一和第二布里渊区。试画出边长为的二维正方格子的第一和第二布里渊

19、区。21 2.7 假设基矢假设基矢 构成简单正交系构成简单正交系 证明晶面族证明晶面族 的面间距为的面间距为 阐明面指数简单的晶面，其面密度比较大，容易解理阐明面指数简单的晶面，其面密度比较大，容易解理c,b,a)(hkl2221/ ( )( )( )hkldabc简单正交系简单正交系cbakcaj bai aa321,倒格子基矢倒格子基矢2311232aabaaa3121232aabaaa1231232aabaaa22kcbjbbiab2,2,2321倒格子矢量倒格子矢量321b lbkbhG222hikjlkabc晶面族晶面族 的面间距的面间距)(hklGd22221/ ( )( )( )

20、hklabc 面指数越简单的晶面，其晶面的间距越大面指数越简单的晶面，其晶面的间距越大 晶面上格点的密度越大，这样的晶面越容易解理晶面上格点的密度越大，这样的晶面越容易解理倒格子基矢倒格子基矢232.10 假设具有立方对称、由同种原子构成的某种晶体，在对其进展假设具有立方对称、由同种原子构成的某种晶体，在对其进展x射线分析时，在衍射谱图中只察看到射线分析时，在衍射谱图中只察看到110、200、220或或222等衍射峰，但没有察看到等衍射峰，但没有察看到100、300、111或或221等衍射峰，试经过分析阐明该晶体具有何种类型的晶体构造。等衍射峰，试经过分析阐明该晶体具有何种类型的晶体构造。 解

21、：对立方对称晶体，有简单立方、体心立方和面心立方三种典型的晶体构造。解：对立方对称晶体，有简单立方、体心立方和面心立方三种典型的晶体构造。对同种原子组成的面心立方晶体，衍射指数全偶或全奇时，衍射强度最强，而衍射指数中部分为奇或部分为偶的衍射峰消逝。对同种原子组成的面心立方晶体，衍射指数全偶或全奇时，衍射强度最强，而衍射指数中部分为奇或部分为偶的衍射峰消逝。200、220或或222衍射峰的的衍射指数全为偶数，但同时出现衍射峰的的衍射指数全为偶数，但同时出现110衍射峰，这是部分为奇和部分为偶的情况，故可判别该晶体并非面心衍射峰，这是部分为奇和部分为偶的情况，故可判别该晶体并非面心立方构造。立方构

22、造。对简单立方，只能出现偶数指数的衍射峰，由于对简单立方，只能出现偶数指数的衍射峰，由于110衍射峰的出现，可判别该晶体并非简单立方构造。衍射峰的出现，可判别该晶体并非简单立方构造。24对同种原子组成的体心立方晶体，晶胞中包含对同种原子组成的体心立方晶体，晶胞中包含2个原子，其中一个在立方体顶角，另一个在立方体体心，它们的坐标分别为个原子，其中一个在立方体顶角，另一个在立方体体心，它们的坐标分别为000和和1/2，1/2，1/2，得到衍射强度为，得到衍射强度为2201cos()sin() hklIfn hkln hkl可见，当衍射指数之和为奇数时，反射消逝，而对于衍射指数之和为偶数时，衍射加强

23、可见，当衍射指数之和为奇数时，反射消逝，而对于衍射指数之和为偶数时，衍射加强110、200、220或或222等衍射峰符合衍射指数之和为偶数的条件衍射加强，而等衍射峰符合衍射指数之和为偶数的条件衍射加强，而100、300、111或或221等衍射峰符合衍射指数之和为奇数的条件反射消逝等衍射峰符合衍射指数之和为奇数的条件反射消逝因此，根据察看到的衍射峰特征可判别该晶体具有体心立方构造。因此，根据察看到的衍射峰特征可判别该晶体具有体心立方构造。252.11 对面心立方的对面心立方的KBr晶体，其中晶体，其中K和和Br离子各自组成一套面心格子，试经过分析论证该晶体的衍射谱图有何特征？离子各自组成一套面心

24、格子，试经过分析论证该晶体的衍射谱图有何特征？解：对面心立方构造的晶体，晶胞中共包含解：对面心立方构造的晶体，晶胞中共包含4个原子，其中一个在立方体顶角，另三个在立方面子心，它们的坐标分别为个原子，其中一个在立方体顶角，另三个在立方面子心，它们的坐标分别为000、1/2，0，1/2、1/2，1/2，0和和0，1/2，1/2，由此得到衍射强度为，由此得到衍射强度为20121cos()cos()cos()sin()sin()sin()hklIffn hkn hln klfn hkn hln kl可见，对于衍射指数中部分为奇或部分为偶时，可见，对于衍射指数中部分为奇或部分为偶时，而对衍射指数全偶或全

25、奇时而对衍射指数全偶或全奇时201hklIff此时衍射强度最小此时衍射强度最小201hklIff衍射强度最强衍射强度最强262.12 从方式上看，从方式上看，KCl非常类似非常类似KBr，但对，但对KCl进展衍射分析时，实验上察看到和进展衍射分析时，实验上察看到和KBr类似的面指数全为偶数的衍射峰，但没有察看到面指数全为类似的面指数全为偶数的衍射峰，但没有察看到面指数全为奇数的衍射峰，为什么？奇数的衍射峰，为什么？答：实验上察看到和答：实验上察看到和KBr类似的面指数全为偶数的衍射峰，阐明类似的面指数全为偶数的衍射峰，阐明KCl晶体具有和晶体具有和KBr类似的面心立方构造，但没有察看到面指数全

26、为奇数的衍射类似的面心立方构造，但没有察看到面指数全为奇数的衍射峰，阐明两者又不完全一样。这是由于峰，阐明两者又不完全一样。这是由于KCl中两种离子的电子数目相等，散射振幅几乎一样，因此，对中两种离子的电子数目相等，散射振幅几乎一样，因此，对X-射线来说，就好似一个晶格常数为射线来说，就好似一个晶格常数为a/2的单原子简单立方晶格，对简单立方晶格，只出现偶数指数的衍射峰。的单原子简单立方晶格，对简单立方晶格，只出现偶数指数的衍射峰。272.13 对由同种原子碳构成的金刚石晶体，试求出衍射强度不为零的条件。对由同种原子碳构成的金刚石晶体，试求出衍射强度不为零的条件。1 1 1( , )4 4 4

27、1 3 3( , )4 4 43 3 1( , )4 4 43 1 3( ,)4 4 4(0,0,0)对于金刚石晶体，选择立方体作为晶胞，那么每个晶胞中共有对于金刚石晶体，选择立方体作为晶胞，那么每个晶胞中共有8个原子，一个在立方体顶角上，坐标为个原子，一个在立方体顶角上，坐标为1 1( ,0)2 211( ,0, )221 1(0, )2 2三个在立方体的面心位置，坐标分别为三个在立方体的面心位置，坐标分别为另外四个在立方体对角线的另外四个在立方体对角线的1/4位置处，坐标分别位置处，坐标分别将这些原子坐标代入式得到衍射强度为将这些原子坐标代入式得到衍射强度为2221 cos()cos()c

28、os()1111cos()cos(33 )cos(33)cos(33 )22221 sin()sin()sin()111sin()sin(33 )sin(33)si222hklIfn hkn kln hln hkln hklnhklnhklfn hkn kln hln hkln hklnhkl21n(33 )2nhkl282221 cos()cos()cos()1111cos()cos(33 )cos(33)cos(33 )22221 sin()sin()sin()111sin()sin(33 )sin(33)si222hklIfn hkn kln hln hkln hklnhklnhklfn

29、 hkn kln hln hkln hklnhkl21n(33 )2nhkl由上式很容易求出衍射强度不为零的条件是：由上式很容易求出衍射强度不为零的条件是：衍射面指数衍射面指数nh、nk和和nl均为奇数；均为奇数；衍射面指数衍射面指数nh、nk和和nl均为偶数且均为偶数且 也为偶数。也为偶数。假设衍射面指数不满足上述两条件，那么衍射消逝。假设衍射面指数不满足上述两条件，那么衍射消逝。1()2n hkl293.1 证明两种一价离子组成一维晶格的马德隆常数证明两种一价离子组成一维晶格的马德隆常数2ln2M 假设参考离子带负电荷，那么正离子取假设参考离子带负电荷，那么正离子取“+、负离子取、负离子取

30、“-R参考离子参考离子11112.234MRRRRR 那么有那么有2源于参考离子左右各有两个间隔相等的源于参考离子左右各有两个间隔相等的离子离子11121.234M 利用利用234ln(1).234xxxxx2ln2M 第三章习题第三章习题30;.3.2 假设一晶体两个离子之间的相互作用能可以表示为假设一晶体两个离子之间的相互作用能可以表示为nmrrru)(计算计算1) 平衡间距平衡间距r02) 结合能结合能W单个原子的单个原子的3) 体弹性模量体弹性模量4) 假设取假设取 计算计算 的值的值 ,eVWnmrnm4,3 . 0,10, 2031;.1) 平衡间距平衡间距r0的计算的计算平衡条件

31、平衡条件)(2)(nmrrNrU00rrdrdU01010nmrnrm2) 单个原子的结合能单个原子的结合能01( )2Wu r 1(1)()2mn mmnWnmmnmnr10)(晶体内能晶体内能00( )()mnr ru rrr 323) 体弹性模量体弹性模量0220)(VVUKV晶体的体积晶体的体积3NArV A为常数，为常数，N为原胞数目为原胞数目VrrUVU1121()23mnNmnrrNAr221121()23mnUNrmnVVrrrNAr)(2)(nmrrNrU晶体内能晶体内能3391200020220220nmnmVVrnrmrnrmVNVU031)(22010100NArrnr

32、mNVUnmVVnmrnrm00体弹性模量体弹性模量0220)(VVUKV由平衡条件由平衡条件912020220220nmVVrnrmVNVU349120020220nmVVrnnrmmVNVU920020nmrrVnmNnmrnrm00)(2000nmrrNU)(9020220UVmnVUVV009VmnUK 体弹性模量体弹性模量0220)(VVUKV912020220220nmVVrnrmVNVU354) 假设取假设取 计算计算 的值的值eVWnmrnm4,3 . 0,10, 20,mnmnr10)(1(1)()2mn mmnWnm1002rW210020Wrr95101.18 10eV

33、m1929.0 10eV mnmrnrm00363.3 设假设一晶体平衡时体积为设假设一晶体平衡时体积为V0，原子间总的相互作用能为，原子间总的相互作用能为U0，假设原子间相互作用能由式，假设原子间相互作用能由式所表述，试证明紧缩系数为所表述，试证明紧缩系数为( )nmU rrr 009nm UV证明：体弹性模量证明：体弹性模量晶体体积晶体体积0202()VUKVV因此，体弹性模量可表示为因此，体弹性模量可表示为 3VN r02201()9r rUKN rr211222(1)(1)(),()22mnmnUNmnUNm mn nrrrrrr0222000222222000000001(1)(1)

34、21122r rmnmnmnmnUNm mn nrrrrNmnmnNmnrrrrrrrr00mnmnrr0002 9mnN nmKVrr0000( )()2mnNU rUrr009nmUV37 3.4 知有知有N个离子组成的个离子组成的NaCl晶体，其结合能为晶体，其结合能为 现以现以 来替代排斥项来替代排斥项 ，且当晶体处于平衡时，且当晶体处于平衡时， 这两者对互作用势能的奉献一样，试求这两者对互作用势能的奉献一样，试求n和和的关系。的关系。 20( )()24nNeU rrrrcenr 将结合能在平衡位置处展开将结合能在平衡位置处展开)()()()(000rrrUrUrUrr38)4(2)

35、( 02rcereNrU以以 替代替代 后后rce0nr)()()( )( 000rrrUrUrUrr根据题意根据题意)( )(00rUrU结合能结合能0)()(00rrrrrUrU00rncer010rnncer3900rncer010rnncernr 01()nen c两式相比两式相比n和和的关系的关系403.5计算面心立方简单格子的计算面心立方简单格子的A6和和A12(1) 只计最近邻；只计最近邻；2计算到次近邻。计算到次近邻。o111角顶角顶o原子周围有原子周围有8个这样的晶胞个这样的晶胞标号为标号为1的原子是原子的原子是原子o的最近邻，总共有的最近邻，总共有12个最近邻，以最近邻间隔

36、度量，那么个最近邻，以最近邻间隔度量，那么aj=122212121jjAa 661jjAa 0 jjra R R为最近邻间隔为最近邻间隔假设只计最近邻那么假设只计最近邻那么661(1)12 ( )121A12121(1)12 ( )121A标号为标号为2的原子是原子的原子是原子o的次近邻，总共有的次近邻，总共有6个次近邻，以最近邻间隔度量，那么个次近邻，以最近邻间隔度量，那么aj=21/2假设计算到次近邻那么假设计算到次近邻那么66611(2)12 ( )6 ()12.7512A 12121211(2)12 ( )6 ()12.09412A 41;.4.1对一维双原子分子链，原子质量均为对一维

37、双原子分子链，原子质量均为m，原子一致编号，任一原子与两最近邻的间距不同，力常数分别为，原子一致编号，任一原子与两最近邻的间距不同，力常数分别为1和和2，晶格常数为，晶格常数为a，求原，求原子的运动方程以及色散关系。子的运动方程以及色散关系。1 2 3n-1 n n+1N-2 N-1 N12第第n-1与第与第n+1个原子属于同一种原子个原子属于同一种原子n+2 n+3 第第n与第与第n+2个原子属于同一种原子个原子属于同一种原子于是于是 第第n个原子受的力为个原子受的力为第第n+1个原子受的力为个原子受的力为2111()()nnnnnfxxxx 112121()()nnnnnfxxxx 第四章

38、习题第四章习题42对每种原子，可写出其运动方程对每种原子，可写出其运动方程221112()()nnnnnd xmxxxxdt 21121212()()nnnnnd xmxxxxdt 将方程的解写成角频率为将方程的解写成角频率为 的简谐振动的方式，即的简谐振动的方式，即12iqnatnxAe121iqnatnxBe432122122112()()0()()0iqaiqamAeBeAmB 2122122112()0()iqaiqameem 22221/21212221221/212122121624sin ()2()2411sin ()()2mqammmqam 色散关系色散关系得到得到A、B非非0

39、解的条件是系数行列式必需为解的条件是系数行列式必需为0，即，即由此得到由此得到12iqnatnxAe121iqnatnxBe代入代入221112()()nnnnnd xmxxxxdt 21121212()()nnnnnd xmxxxxdt 444.2 问长光学支格波与长声学支格波在本质上有何区别？问长光学支格波与长声学支格波在本质上有何区别？长光学支格波的特征是每个原胞内的不同原子做相对振动，振动频率较高，包含了晶格振动频率最高的振动方式。长光学支格波的特征是每个原胞内的不同原子做相对振动，振动频率较高，包含了晶格振动频率最高的振动方式。长声学支格波的特征是原胞内的不同原子没有相对位移，原胞做

40、整体振动，振动频率较低，包含了晶格振动频率最低的振动方式。长声学支格波的特征是原胞内的不同原子没有相对位移，原胞做整体振动，振动频率较低，包含了晶格振动频率最低的振动方式。任何晶体都存在声学支格波，但简单晶格晶体不存在光学支格波。任何晶体都存在声学支格波，但简单晶格晶体不存在光学支格波。454.3 按德拜模型试计算晶体中的声子数目，并对高温暖很低温度两种情况分别进展讨论。按德拜模型试计算晶体中的声子数目，并对高温暖很低温度两种情况分别进展讨论。频率为频率为的格波的声子数的格波的声子数/1( )1kTne对德拜模型，方式密度或频率分布函数为对德拜模型，方式密度或频率分布函数为2233( )2Vg

41、C那么总的声子数那么总的声子数0( ) ( )DNngd/20231312DkTVdeC高温高温/0kT/1/kTekT /1( )/1kTnkTe所以高温时声子数为所以高温时声子数为22334DVkNTC46/23021312DkTVNdeC很低温度很低温度/ kT 作变量变换作变量变换/xkT 332233032(1)xVk T x dxCe2/2301312DkTVNdeC3AT332233032(1)xVkT x dxAconstCe474.4 设一长度为设一长度为L的一维简单晶格，原子质量为的一维简单晶格，原子质量为m，原子间距为，原子间距为a，原子间的相互作用势可表示成，原子间的相

42、互作用势可表示成试由简谐近似求试由简谐近似求1色散关系；色散关系；2方式密度方式密度D；3晶格比热。晶格比热。()cos( )U aAa 1色散关系色散关系()cos( )U aAa 22022()()ad Ud Udrd 恢复力常数恢复力常数2022()d UAda 2sin()2qam 代入代入得到色散关系为得到色散关系为2sin()2Aqaam 48设单原子链长度设单原子链长度波矢取值波矢取值hNaq2每个波矢的宽度每个波矢的宽度2Na形状密度形状密度Na2dq间隔内的形状数间隔内的形状数dqNa2 对应对应q， 取值一样，取值一样， d 间隔内的形状数目间隔内的形状数目dqNad22)

43、(LNa2方式密度方式密度D 49dqNad22)(一维单原子链色散关系一维单原子链色散关系)2(sin422aqmm40)2sin(0aq令令两边微分得到两边微分得到dqaqad)2cos(202021)2cos(aqdqad2202d 间隔内的形状数目间隔内的形状数目502202dadqdN2201222012)(Ndqad2202代入代入dqNad22)( 一维单原子链的频率分布函数一维单原子链的频率分布函数513晶格比热晶格比热频率为频率为 的格波的热振动能为的格波的热振动能为/1Bk Te整个晶格的热振动能为整个晶格的热振动能为0/0( )1Bk TEde VdECdT22012)(

44、N02/222002()(1)BVBk TBLdCkak Te 524.5 设晶体中每个振子的零点振动能为设晶体中每个振子的零点振动能为 ，试用德拜模型求晶体的零点振动能，试用德拜模型求晶体的零点振动能 12根据量子力学零点能是谐振子所固有的，与温度无关，故根据量子力学零点能是谐振子所固有的，与温度无关，故T=0K时振动能时振动能E0就是各振动模零点能之和就是各振动模零点能之和 000mEEgd 012E 22332sVgv42339168mmsVNv534.6 假设原子分开平衡位置位移后的势能为假设原子分开平衡位置位移后的势能为如用经典实际，试证明比热为：如用经典实际，试证明比热为： 234

45、( )Ucgf2233151()28VBBfgCkk Tcc544.7 假设晶体总的自在能可表示为假设晶体总的自在能可表示为其中其中 表示晶格振动对系统自在能的奉献，表示晶格振动对系统自在能的奉献， 是绝对零度时系统的内能，假设是绝对零度时系统的内能，假设 可表示可表示其中其中 是德拜温度，试证明：是德拜温度，试证明：1压力压力 ， 为格林爱森常数；为格林爱森常数；2线膨胀系数线膨胀系数 0( )( , )vFU VF T VvF0( )U VvF()DvFTfTD0(/)(1/)DUfTPVVT lnlnDddV 3VCVK554.81温度一定时，问一个光学波的声子数目和一个温度一定时，问一

46、个光学波的声子数目和一个 声学波的声子数目哪个多？声学波的声子数目哪个多？ 2对同一个振动方式，问温度高时的声子数目和对同一个振动方式，问温度高时的声子数目和 温度低时的声子数目哪个多？温度低时的声子数目哪个多？频率为频率为 的格波的平均声子数为的格波的平均声子数为/1( )1kTne1光学波的频率总是比声学波的频率高，所以，温度一定时，一个光学波的声子数目少于一个声学波的声子数目光学波的频率总是比声学波的频率高，所以，温度一定时，一个光学波的声子数目少于一个声学波的声子数目2温度高时的声子数目多于温度时的声子数目温度高时的声子数目多于温度时的声子数目/1()1HHkTn Te/1()1LLk

47、Tn Te565.1 试问绝对零度时价电子与晶格能否交换能量？试问绝对零度时价电子与晶格能否交换能量？晶格的振动构成格波，价电子与晶格交换能量，实践上是价电子与格波交换能量，格波的能量子称为声子，因此，价电子与格波交换能晶格的振动构成格波，价电子与晶格交换能量，实践上是价电子与格波交换能量，格波的能量子称为声子，因此，价电子与格波交换能量可看成是价电子与声子交换能量。量可看成是价电子与声子交换能量。频率为频率为的格波的声子数的格波的声子数/1( )1kTne绝对零度时，任何频率的格波的声子全部消逝，因此，绝对零度时价电子与晶格不再交换能量。绝对零度时，任何频率的格波的声子全部消逝，因此，绝对零

48、度时价电子与晶格不再交换能量。第五章习题第五章习题57;.5.2 试问晶体膨胀时费米能级如何变化？试问晶体膨胀时费米能级如何变化？费米能级费米能级202/3(3)2FEnm晶体膨胀时，体积变大，但电子数目不变，故晶体膨胀时，体积变大，但电子数目不变，故n变小，因此，费变小，因此，费米能级降低。米能级降低。58;.5.3 试问为什么价电子的浓度越高，电导率越高？试问为什么价电子的浓度越高，电导率越高？2nem从公式看，电导率正比于价电子的浓度，因此，价电子浓度越高，电导率就越高从公式看，电导率正比于价电子的浓度，因此，价电子浓度越高，电导率就越高然而，并非一切价电子都参与导电，仅仅费米面附近的电

49、子才参与对导电的奉献，因此，费米球越大，对导电有奉献的电子然而，并非一切价电子都参与导电，仅仅费米面附近的电子才参与对导电的奉献，因此，费米球越大，对导电有奉献的电子数目就越多，而费米球的半径数目就越多，而费米球的半径021/3(3)Fkn可见，电子浓度越高，费米球就越大，对导电有奉献的电子什么也就越多，因此，电导率就越高可见，电子浓度越高，费米球就越大，对导电有奉献的电子什么也就越多，因此，电导率就越高59;.5.4 假设二维电子气的能态密度假设二维电子气的能态密度 试证明费米能为试证明费米能为 其中其中n为单位面积的电子数。为单位面积的电子数。2( )mN E2/ln1Bnmk TFBEk

50、 Te单位面积金属的电子总数为单位面积金属的电子总数为0( ) ( )nN E f E dE2( )mN E()/1( )1FBE Ek Tf Ee()/2011FBE Ek TmndEe/2ln(1)FBEk TBmk Te2/1FBBnEk Tmk Tee2/ln1Bnmk TFBEk Te60;.5.5 试求一维金属中自在电子的能态密度、费米能级、电子平均动能以及一个电子对比热的奉献。试求一维金属中自在电子的能态密度、费米能级、电子平均动能以及一个电子对比热的奉献。设一维金属中有设一维金属中有N个导电电子，晶格常数为个导电电子，晶格常数为a，那么形状密度为，那么形状密度为2222km d

51、EdkmE2再由E得到1/22( )dzNamg EEdE能态密度能态密度222Nadzdk那么在那么在kk+dk范围内电子数为范围内电子数为2Na1/22NamdzEdE在在EE+dE内电子数为内电子数为61;.绝对零度时费米能级以下一切态被电子占据，故有绝对零度时费米能级以下一切态被电子占据，故有0001/200222( )FFEEFNamENamNg E dEEdE202()8FEma平均一个电子所具有的能量平均一个电子所具有的能量00( ) ( )NEdzEf E g E dEENN1/202( )amf E EdE23/2222() 38FBFamEEk TE62;.平均一个电子对比

52、热的奉献为平均一个电子对比热的奉献为23/2222() 38FBFamEEk TE2222()()3124eVVBBBFFEamTCk TkkTTE63;.5.6 试求二维金属中自在电子的能态密度、费米能级、电子平均动能以及一个电子对比热的奉献。试求二维金属中自在电子的能态密度、费米能级、电子平均动能以及一个电子对比热的奉献。设二维金属的面积为设二维金属的面积为S，那么形状密度为，那么形状密度为222kmkdkdEm2再由E得到2( )dzmSg EdE能态密度能态密度222(2 )Sdzkdk那么在那么在kk+dk范围内电子数为范围内电子数为2(2 )S2222(2 )SmdEdz在在EE+

53、dE内电子数为内电子数为64;.绝对零度时费米能级以下一切态被电子占据，故有绝对零度时费米能级以下一切态被电子占据，故有0002200( )FFEEFmSmSNg E dEdEE20FnEm平均一个电子所具有的能量平均一个电子所具有的能量00( ) ( )NEdzEf E g E dEENN20( )mf E EdEn2222() 23FBmEEk TnNnS平均一个电子对比热的奉献为平均一个电子对比热的奉献为2()()3eVVBFETCkTT65;.5.7 证明，当证明，当 时，电子数目每添加一个，时，电子数目每添加一个， 那么费米能变化为那么费米能变化为 其中其中 为费米能级处的能态密度。

54、为费米能级处的能态密度。0BFk TE001()FFEg E0()Fg E222/30(3)2FnEm2/3AN222/3(3/)2VAm电子数目每添加一个，费米能的变化电子数目每添加一个，费米能的变化02/32/3(1)FEA NAN2/32/3(1 1/)1ANN2/32(1) 13ANN1/323AN02/31/32/32233FEANNNN03/22()3FNC E003/20011()()FFFFEC Eg ECE66;.5.8 每个原子占据的体积为每个原子占据的体积为a3，绝对零度时价电子的费米半，绝对零度时价电子的费米半 径为径为 ，计算每个原子的价电子数目，计算每个原子的价电子

55、数目02 1/3(6)/Fka021/3(3)Fkn根据自在电子气模型，绝对零度时费米半径为根据自在电子气模型，绝对零度时费米半径为而知金属绝对零度时费米半径为而知金属绝对零度时费米半径为02 1/3(6)/Fka23 1/3(6/)a21/332(3)a两者比较可知电子密度为两者比较可知电子密度为32na因此该金属的原子具有两个价电子因此该金属的原子具有两个价电子67;.310.5/mg cm661.61 10(295)0.038 10(20)cmTKcmTK 银的质量密度银的质量密度 原子量原子量 电阻率电阻率 107.875.9 假设将银看成具有球形费米面的单价金属假设将银看成具有球形费

56、米面的单价金属 计算以下各量计算以下各量1) 费密能量和费密温度费密能量和费密温度2) 费密球半径费密球半径3) 费密速度费密速度4) 在室温以及低温时电子的平均自在程在室温以及低温时电子的平均自在程68 1) 费密能量和费密温度费密能量和费密温度2022/3(3)2FEnm6293313410.5100.586 10/107.879.11 101.05 10AAmNnNmmkgJ sM0198.82 105.5FEJeV046.4 10FFBETKk费密能量费密能量费密温度费密温度210/3(3)Fkn692) 费密球半径费密球半径020()2FFkEm0022FFmEk 01011.2 1

57、0Fkm0198.82 10FEJ3) 费密速度费密速度0FFkvm61.38 10/Fvm s704) 在室温以及低温时电子的平均自在程在室温以及低温时电子的平均自在程120()1FneEm02()FmEne0()FFlvE2Fkne01011.2 10FFkkm电导率电导率驰豫时间驰豫时间平均自在程平均自在程2Fmvlne0 K到室温之间的费密半径变化很小到室温之间的费密半径变化很小7102Fklne平均自在程平均自在程1929334010162956201.6 100.586 10/1.05 101.2 101.61 100.038 10FTKTKeCnmJ skmcmcm8295632

58、05.24 1052.42.2 102.210TKTKlmnmlmnm726.1 电子在周期场中的势能函数电子在周期场中的势能函数bnaxbanbnaxbnanaxbmxV) 1(0)(21)(222 且且a=4b， 是常数。是常数。1) 画出此势能曲线，并计算势能的平均值；画出此势能曲线，并计算势能的平均值；2) 用近自在电子模型用近自在电子模型 计算晶体的第一个和第二个带隙宽度计算晶体的第一个和第二个带隙宽度 第六章习题第六章习题73bnaxbanbnaxbnanaxbmxV) 1(0)(21)(222( )V x2a-b2a2a+b(n-1)a-b(n-1)a+b(n-1)ana-bna

59、+bna(n+1)a-b(n+1)a+b(n+1)a-b0b74 势能的平均值势能的平均值LikxikxdxeLxVeLV01)(1222111() 2na bikxikxna bVNembxnae dxLLLNa75势能的平均值势能的平均值222111() 2na bikxikxna bVNembxnae dxLL222() 2na bna bNVmbxnadxL令令nax 2221()2bbVmbda2296aVm76近自在电子近似中，势能函数的第近自在电子近似中，势能函数的第n个傅里叶系数个傅里叶系数 2/2/21( )inxaanaVV x edxa禁带宽带禁带宽带,2g nnEV第一

60、带隙宽度第一带隙宽度2/211/2122( )ixaagaEVV x edxa222222218242ixbabmmbbx edxb第二带隙宽度第二带隙宽度4/222/2122( )ixaagaEVV x edxa2222221242ixbbbmmbbx edxb77axxksin)() 1mmkmaxfix)()()()2axixk3cos)() 3lklaxfx)()()46.2 对于一维周期势场中运动的电子，试求电子处在以下态中的的波矢对于一维周期势场中运动的电子，试求电子处在以下态中的的波矢 其中其中a是晶格常数是晶格常数 78根据布洛赫定理根据布洛赫定理)()(reRrnRk in一