(完整word版)平稳随机过程的采样和插值

1、随机信号实验平稳随机过程的采样和插值.实验目的了解确定信号的采样与平稳随机信号的采样之间的关系，掌握信号的采样及分析方法。实验原理确定信号的采样符合香农定理，那么随机信号的采样是否符合香农定理呢？答案是定 的。香农定理可以推广到随机信号的采样。若x(t)为平稳随机过程，且具有零均值，它的功率谱密度sx( )限于(-飞，+ C)之间。当满足条件X(t)专im X(nT)sin( tctn)n 严 nco ct n 兀上式就是平稳随机过程的采样定理。式中T为采样周期。三.实验任务与要求 程序用matlab或C/C+语言编写和仿真。系统框图如图29、图30所示:图29抽样系统框图图30插值系统框图

2、输入信号x(t) : x(t)=正弦波信号+n(t),频率为100Hz的正弦波信号，幅值为1v, n(t)为白噪声。计算输入信号的均值、均方值、方差、相关函数、概率密度、频谱及功率谱 密度、相关函数。低通滤波器设计低通滤波器技术要求：通带截止频率1KHz阻带截止频率2KHz=过渡带：1KHz 阻带衰减：35DB通带衰减：1DB 米样频率：W 44.1KHZ计算经低通滤波器后信号的均值、均方值、方差、相关函数、频谱及功率谱密度、相关函数。 对输入信号进行抽样：采样频率8000Hz。每间隔4个点和每间隔8个点各抽样一次。计算抽样信号的均值、均方值、方差、相关函数、频谱及功率谱密度、相关函数。 对采

3、样信号进行插值：每一个间隔插入4个值和每一个间隔插入 8个值。采样频率8000Hz。计算插值信号的均值、均方值、方差、相关函数、频谱及功率谱密度、相关函数。对采样前后、插值前插值后信号进行比较。观察在采样频率不变的情况下，信号频谱的变化和频谱的周期延拓性。 讨论X(n)的自相关函数、功率谱密度与X(t)的自相关函数、功率谱密度之间的关系。3四实验步骤及结果1 .输入信号x(t)(1) x(t)=正弦波信号+n(t)，频率为 为高斯白噪声。Fs=40000;Ns=5000 ;n=0:Ns-1;t=n/Fs;sin e=si n(2*pi*100*t);no ise=ra ndn (1,le ng

4、th(t);x=s ine+no ise;figure(1);plot(t,x);xlabel( t ),ylabel( x);title( 输入信号)；100Hz的正弦波信号，幅值为 1v,其中n (t )两点间距取1/40000 ，共取N=5000个采样点,n为长度为N的序列，t为采样时间，作为 信号图像横坐标产生频率为100hz的正弦波产生高斯白噪声信号合成为输入信号产生的输入信号如下:输入信号4-40.145 Il00.020.040.060.080.10.12t(2) 计算输入信号的均值、均方值、方差均值： x_mean = 0.0072均方值：x_var = 1.4747方差：in

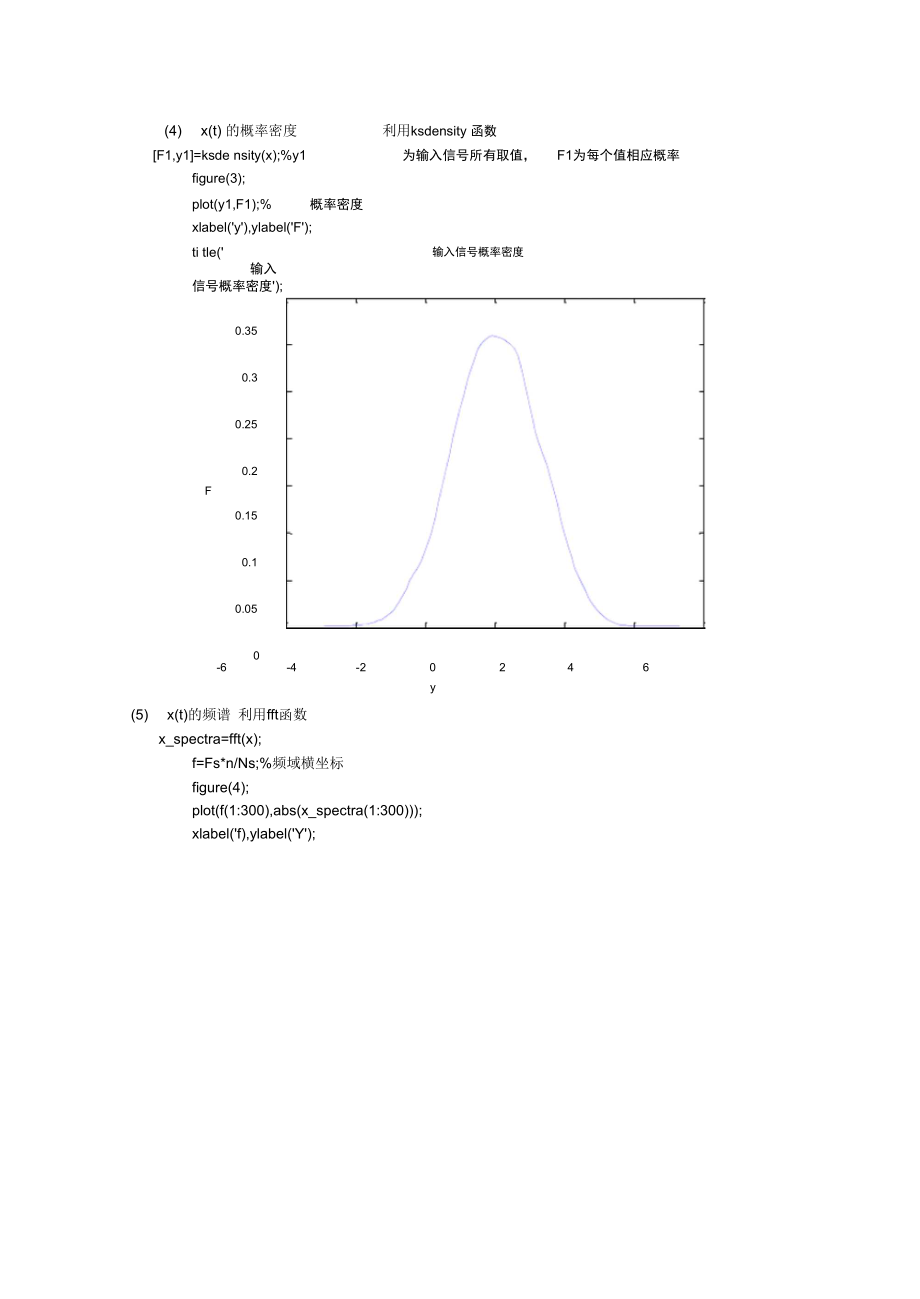
5、 put_fa ngcha =1.4748(3) x(t)的相关函数利用MALTLA中的xcorr函数 x_xcorr=xcorr(x);t1=(-Ns+1:Ns-1)/Fs;%相关函数图像横坐标figure(2);plot(t1,x_xcorr);%相关函数xlabel(t),ylabel(R);title(输入信号相关函数)；t(4) x(t) 的概率密度利用ksdensity 函数F1,y1=ksde nsity(x);%y1为输入信号所有取值，F1为每个值相应概率figure(3);plot(y1,F1);%概率密度xlabel(y),ylabel(F);输入信号概率密度ti tle(

6、输入信号概率密度);0.350.30.250.2F0.150.10.050-6-4-20246y(5) x(t)的频谱 利用fft函数x_spectra=fft(x);f=Fs*n/Ns;%频域横坐标figure(4);plot(f(1:300),abs(x_spectra(1:300);xlabel(f),ylabel(Y);输入信号频谱输入信号频谱title(输入信号频谱);1600140012001000Y 8006004002000 -05001000150020002500f(6) x(t)的功率谱密度用功率谱的概念求，即频谱函数的平方求时间平均。P仁x_spectra.*conj(

7、x_spect/Ns;%频谱函数的平方求时间平均figure(5);plot(f(1:300),abs(P1(1:300);%功率谱密度xlabel(f),ylabel(S);title(输入信号功率谱密度)600输入信号功率谱密度50040030020010005001000150020002500f2 滤波器的设计设计思路是：用巴特沃斯模拟滤波器生成数字滤波器，并画出滤波器的频谱。程序如下：fp=1000;fs=2000;rp=1;rs=35;Fs1=40000;wp=2*pi*fp/Fs1;ws=2*pi*fs/Fs1;wap=ta n( wp/2);was=ta n( ws/2);Fs

8、1=Fs1/Fs1;N,Wn=buttord(wap,was,rp,rs,s);z,p,k=buttap(N);bp,ap=zp2tf( z,p,k);%得到传输函数bs,as=lp2lp(bp,ap,wap);%低通到低通，频谱变换bz,az=bili near(bs,as,Fs1/2); %将模拟滤波器传递函数转为数字滤波器传递函数H,w=freqz(b z,az,256,Fs1*10000);%特性分析figure(6)plot(w,abs(H);%画出数字滤波器的波形图title(低通滤波器的频谱);xlabel(f/hz);grid on;低通滤波器的频谱3. x(t)通过滤波器的信

9、号y(1) 输出y的波形及均值，均方值，方差y=filter(bz,az,x)13通过低通滤波器的波形0.14均值：0.0416均方值：0.7248方差：0.7265(2) 输出y的相关函数程序类似求x(t)的相关函数，其波形如下:t(3) y的概率密度程序类似求x(t)的概率密度，其波形如下：输出信号概率密度y输岀信号频谱2500(4) y的频谱程序类似求x(t)的频谱，其波形如下：1600140012001000丫 80060040020000500100015002000f(5) y的功率谱密度900800700600500400300200100500输岀信号功率谱密度10001500

10、2000250030004对y信号进行抽样 采样频率8000Hz若8000hz采样，波形输出程序为：sample仁zeros(1,ceil(le ngth(t)/(Fs/fs1);i=1;for k=1:le ngth(t)if mod(k,(Fs/fs1)=1sample1(i)=y(k);i=i+1;endendfigure(12);stem(t2,sample1);%除去相邻采样点间零点的采样信号xlabel(t),ylabel(y);title(采样信号);则波形为：米样信号1.500.020.040.060.080.1t0.1215(1)每间隔4个点抽样一次 4采样波形及均值，均方值

11、，方差程序代码如下：sample2=zeros(1,ceil(le ngth(t)/(Fs/fs1);for k=1:le ngth(t2)if mod(k,5)=1sample2(k)=sample(k);elsesample2(k)=0;endendsample3=zeros(1,ceil(le ngth(t)/(Fs/fs1)/5);i=1;for k=1:5:le ngth(t2)sample3(i)=sample1(k);i=i+1;endfigure(13);stem(1:le ngth(t2)/5)/300,sample3);%除去相邻采样点间零点的采样信xlabel(t),yl

12、abel(y);title(4 采样信号);sampleunzhi4=mean(sample2)% 均值sample_fa ngcha4=std(sample2)% 方差sampleunfan gzhi4=sample_fa ngcha4+sample_j un zhi4.A2%均方值4采样信号为：均值：-0.0125方差:0.3212均方值：0.3213 4采样信号的相关函数代码函数如上t#4采样信号的概率密度y4采样信号的频谱4米样信号频谱4采样信号的功率谱密度174采样信号功率谱密度(2) 每间隔8个点抽样一次程序和4采样类似，只是间隔 8个点采样信号8米样信号t0238米样信号相关函数

13、8米样信号概率密度均值：-7.0098e-004均方值：0.1099方差：0.1099 8采样信号的相关函数108642R0-2-4-6-8-1000-800-600-400-20002004006008001000t 8采样信号的概率密度0.70.60.50.4F0.30.20.1-4-3-2-101234y 8采样信号的频谱109876丫 5432108米样信号频谱05001000f1500 8采样信号的功率谱密度8采样信号功率谱密度f4对信号进行插值采样频率为 8000Hz插值思路：用三次多项式插值法( 1)每一个间隔插入 4 个值 每间隔插入 4 个值波形及均值，均方值，方差 程序如下

14、：t4=zeros(1,(length(t2)-1)*4+length(t2);% 插值信号横坐标 for k=1:length(t4)if mod(k,5)=1 t4(k)=(1/fs1)*fix(k/5);endif mod(k,5)=2 t4(k)=(1/fs1)*fix(k/5)+(1/fs1)/5;endif mod(k,5)=3 t4(k)=(1/fs1)*fix(k/5)+(2/fs1)/5;endif mod(k,5)=4 t4(k)=(1/fs1)*fix(k/5)+(3/fs1)/5;endif mod(k,5)=0 t4(k)=(1/fs1)*(k/5-1)+(4/fs1

15、)/5;endend inter4=interp1(t2,sample1,t4,cubic);figure(23)stem(t4,inter4);% 插值信号 xlabel(t),ylabel(y);title(4 插值信号 );figure(80)plot(t4,inter4);% 插值信号 xlabel(t),ylabel(y);title(4 插值信号 );disp(4 插值信号均值 :); inter4_mean=mean(inter4);% 均值 disp(4 插值信号方差 :);inter4_var=var(inter4);% 方差disp(4 插值信号均方值 :);in ter4

16、_rms=i nter4_var+i nter4_mea n42;%均方值均值： -0.0067均方值： 0.5573方差： 0.557327插值信号为:y4插值信号t 每间隔插入4个值波形的相关函数4插值信号相关函数-0.2-0.15-0.1-0.0500.050.10.15t 每间隔插入4个值波形的概率密度y 每间隔插入4个值波形的频谱f1=5*fs1*(0:le ngth(t4)-1)/le ngth(t4);%频域横坐标in ter4_spectra=fft(i nter4);figure(26);plot(f1(1:300),abs(i nter4_spectra(1:300);%频

17、谱xlabel(f),ylabel(Y);title(4插值信号频谱);频谱波形为：20001800160014001200100080060040020004插值信号频谱5001000150020002500f3000 每间隔插入4个值波形的功率谱密度P5=i nter4_spectra.*conj(i nter4_spectra)/le ngth(t4);figure(27);plot(f1(1:300),P5(1:300);% 功率谱密度 xlabel(f),ylabel(S);title(4插值信号功率谱密度);9008007006005004003002004插值信号功率谱密度500

18、100015002000250030001000f29(2 )每一个间隔插入8个值每间隔插入8个值波形及均值，均方值，方差8插值信号均值：-0.0067均方值：0.5572方差：0.5573 每间隔插入8个值波形的相关函数t43 每间隔插入8个值波形的概率密度 每间隔插入8个值波形的频谱8米样信号频谱10 -1 9 -一8 -II7 -1一116|1 J! !；1丫 5 -1 11/:1I Uli； flJJ1 -.14亠 1|r1I111 |I*11=1II 13 -11|1 -1 1 1 11 11 1;12 -|111 11 1M HI11 li /J J讣1 tj/1* V 1,/?.

19、 19V, ifi 1E/1 J i0 Lrbr1050010001500f 每间隔插入8个值波形的功率谱密度8插值信号功率谱密度16001400 -1200 -1000 -S 800 -600400 -200、5001000150020002500300000五：实验结果分析(1)针对问题(6),对采样前后、插值前插值后信号进行比较。观察在采样频率不变的情况下，信号频谱的变化和频谱的周期延拓性。 问题分析由随机信号和DSP相关知识知道，对于时间连续但幅度不连续的信号，其DTFT是以采样频率为周期延拓的连续信号，幅度衰减为被采样信号的1/T。插值时则相反。因此对采样前后的信号， 根据上述结论可

20、得，在采样后信号的频谱是以采样角频率为周期延拓的。由于信号最初经过 40000hz的采样处理，经过滤波器后对输入信号进行了8000HZ的采样，在8000HZ勺基础上在进行4间隔采样，8间隔采样。此处8000HZ处理信号为采样前信 号，因此4间隔采样后的信号频谱减小为采样前信号的频谱周期的1/5 ,其幅度也减小为采样前信号的1/5。同理对8间隔采样后的信号频谱减小为采样前信号的频谱周期的1/9，其幅度也减小为采样前信号的1/9，对插4点后的信号频谱增为插值前信号的频谱周期的5倍，其幅度也增大为插值前信号的 5倍。对插8点后的信号频谱增为插值前信号的频谱周期的9倍，其幅度也增大为插值前信号的9倍。

21、 实际图像分析：4采样信号频谱f40011ra1.350-300250Y 200150-10050 一0诫叽4卅8000言号频谱010002000300040005000600070008000f由图像分析可见其完全符合理论分析。 讨论X(n)的自相关函数、功率谱密度与X(t)的自相关函数、功率谱密度之间的关系。问题分析由DSP目关知识知道，对于时间连续但幅度不连续的信号，其DTFT是以采样频率为周期延拓的连续信号，幅度衰减为被采样信号的1/T。插值时则相反。并且自相关函数和功率谱密度互为一对傅里叶变换对。因此对采样前后的信号，根据上述结论可得，4间隔采样后的信号频谱减小为采样前信号的频谱的1

22、/5 ,由于功率谱密度是频谱平方的时间平均，其幅度减小为采样前信号的1/25。同理对8间隔采样后的信号频谱减小为采样前信号的1/9，其功率谱密度减小为采样前信号的频谱周期的1/81 ,对插4点后的信号频谱增为插值前信号的频谱的 5倍，其幅度也增大为插值 前信号的25倍。对插8点后的信号频谱增为插值前信号的频谱的 9倍，其幅度也增大为插值前信号的81倍。对于自相关函数，由于其是频谱的傅里叶反变换，对于4采样信号的自相关函数其幅度是采样前的1/5，对于8采样信号的自相关函数其幅度是采样前的 1/9。同样对于4和8插值信 号，其自相关函数幅度分别为采样前的5倍和9倍实际图像分析：ttS8000信号功

23、率谱密度3530252015105001000150020002500f30001.61.41.21S 0.80.60.40.200100020003000400050006000f由图像分析可见其完全符合理论分析。六源程序%生成输入信号Fs=40000;Ns=4096;n=0:Ns-1;t=n/Fs;% 用离散序列模拟的正弦信号两点间距取 1/40000 ，共 取N=5000个采样点,n为长度为N勺序列，t为采样时间，作为信号图像横坐标 sine=sin(2*pi*100*t);% 要求的正弦信号noise=randn(1,length(t);% 高斯白噪声 x=sine+noise; %

24、合成输入信号 figure(1);plot(t,x);% 输入信号图形 xlabel(t),ylabel(x);title( 输入信号 );% disp( 输入信号均值 :);x_mea n=mea n( x)%均值disp( 输入信号方差 :);x_var=var(x)% 方差disp( 输入信号均方值 :)in put_fa ngcha=x_var+x_mea n. A2%均方值%求相关函数和概率密度以及频谱 x_xcorr=xcorr(x);t1=(-Ns+1:Ns-1)/Fs;% 相关函数图像横坐标figure(2); plot(t1,x_xcorr);% 相关函数 xlabel(t)

25、,ylabel(R);title( 输入信号相关函数 );F1,y1=ksde nsity(x);%y1为输入信号所有取值，F1为每个值相应概率figure(3);plot(y1,F1);% 概率密度 xlabel(y),ylabel(F);title( 输入信号概率密度 );x_spectra=fft(x);f=Fs*n/Ns;% 频域横坐标 figure(4);plot(f(1:300),abs(x_spectra(1:300);%频谱xlabel(f),ylabel(Y);title( 输入信号频谱 );P1=x_spectra.*conj(x_spectra)/Ns;% 频谱函数勺平方

26、求时间平均figure(5); plot(f(1:300),abs(P1(1:300);%功率谱密度xlabel(f),ylabel(S);title( 输入信号功率谱密度 );%hh%生成数字滤波器%巴特沃斯模拟滤波器生成数字滤波器 fp=1000;fs=2000;rp=1;rs=35;Fs1=40000;wp=2*pi*fp/Fs1;ws=2*pi*fs/Fs1;wap=tan(wp/2);was=tan(ws/2);Fs1=Fs1/Fs1;N,Wn=buttord(wap,was,rp,rs,s);z,p,k=buttap(N);bp,ap=zp2tf(z,p,k);% 得到传输函数bs

27、,as=lp2lp(bp,ap,wap);% 低通到低通，频谱变换bz,az=bilinear(bs,as,Fs1/2); % 将模拟滤波器传递函数转换为数字滤波器传递函数 H,w=freqz(bz,az,256,Fs1*10000);% 特性分析figure(6)plot(w,abs(H);% 画出数字滤波器的波形图title( 低通滤波器的频谱 );xlabel(f/hz);grid on;%信号通过低通滤波器y=filter(bz,az,x);y_junzhi=mean(y);% 均值y_fangcha=std(y);% 方差y_junfan gzhi=y_fa ngcha+y_j un

28、 zhi.A2;%均方值figure(7)plot(t,y);title( 通过低通滤波器的波形 );%求相关函数y_xcorr=xcorr(y);t1=(-Ns+1:Ns-1)/40000;% 相关函数图像横坐标figure(8);plot(t1,y_xcorr);% 相关函数xlabel(t),ylabel(R);title( 输出信号相关函数 );%求概率密度F2,y2=ksde nsity(y);%y1为输入信号所有取值，F1为每个值相应概率figure(9);plot(y2,F2);% 概率密度xlabel(y),ylabel(F);title( 输出信号概率密度 );%求频谱y_s

29、pectra=fft(y);f=40000*n/Ns;% 频域横坐标figure(10);plot(f(1:300),abs(y_spectra(1:300);%频谱%plot(abs(y_spectra);xlabel(f),ylabel(Y);title( 输出信号频谱 );%求功率谱密度P2=y_spectra.*conj(y_spectra)/Ns;% 频谱函数的平方求时间平均 figure(11);plot(f(1:300),abs(P2(1:300);%功率谱密度xlabel(f),ylabel(S);title( 输出信号功率谱密度 );%fs1=8000;% 采样周期取 800

30、0Hzt2=(0:Fs/fs1:Ns-1)/Fs;% 采样信号横坐标sample=zeros(1,length(t);for k=1:length(t)if mod(k,(Fs/fs1)=1 sample(k)=y(k);elsesample(k)=0;enden d%未除去相邻采样点间零点的采样信号，为计算频谱和功率谱准备%sample1=zeros(1,ceil(length(t)/(Fs/fs1);i=1;for k=1:length(t)if mod(k,(Fs/fs1)=1sample1(i)=y(k);i=i+1;endendfigure(12);stem(t2,sample1);

31、% 除去相邻采样点间零点的采样信号 xlabel(t),ylabel(y);title( 采样信号 );% %k_spectra=fft(sample);f=Fs*n/Ns;% 频域横坐标 figure(1221);plot(f(1:800),abs(k_spectra(1:800);% 频谱 xlabel(f),ylabel(Y);title(8000 信号频谱 );% k_xcorr=xcorr(sample);t1=(-Ns+1:Ns-1)/Fs;% 相关函数图像横坐标 figure(11111);plot(t1,k_xcorr);% 相关函数 xlabel(t),ylabel(R);t

32、itle(8000 信号相关函数 );%q1=k_spectra.*conj(k_spectra)/Ns;% 频谱函数的平方求时间平均 figure(22222);plot(f(1:1000),abs(q1(1:1000);% 功率谱密度 xlabel(f),ylabel(S);title(8000 信号功率谱密度 );%间隔四点抽样 sample2=zeros(1,ceil(length(t)/(Fs/fs1);for k=1:length(t2)if mod(k,5)=1 sample2(k)=sample(k);else sample2(k)=0;endendsample3=zeros(

33、1,ceil(length(t)/(Fs/fs1)/5);i=1;for k=1:5:length(t2)sample3(i)=sample1(k);i=i+1;endfigure(13);stem(1:length(t2)/5)/300,sample3);% 除去相邻采样点间零点的采样信号 xlabel(t),ylabel(y);title(4 采样信号 );%sample_junzhi4=mean(sample2)% 均值sample_fangcha4=std(sample2)% 方差sampleunfan gzhi4=sample_fa ngcha4+sample_j un zhi4.A

34、2%均方值%sample_xcorr4=xcorr(sample2);t3=(-Ns+1)*fs1/Fs:(Ns-1)*fs1/Fs;% 相关函数图像横坐标figure(14);plot(t3,sample_xcorr4);% 相关函数 xlabel(t),ylabel(R);title(4 采样信号相关函数 );%求概率密度F2,y2=ksde nsity(sample2);%y1为输入信号所有取值，F1为每个值相应概率figure(15);plot(y2,F2);% 概率密度xlabel(y),ylabel(F);title(4 采样信号概率密度 );%求频谱sample_spectra4

35、=fft(sample2);f=40000*n/Ns;% 频域横坐标figure(16);plot(f(1:800),abs(sample_spectra4(1:800);%频谱%plot(abs(y_spectra);xlabel(f),ylabel(Y);title(4 采样信号频谱 );%求功率谱密度P2=sample_spectra4.*conj(sample_spectra4)/Ns;% 频谱函数的平方求时间平均 figure(17);plot(f(1:800),abs(P2(1:800);% 功率谱密度 xlabel(f),ylabel(S);title(4 采样信号功率谱密度 )

36、;%间%隔 8点抽样 sample4=zeros(1,ceil(length(t)/(Fs/fs1);for k=1:length(t2)if mod(k,9)=1 sample4(k)=sample(k);elsesample4(k)=0;endend sample5=zeros(1,ceil(length(t)/(Fs/fs1)/9);i=1;for k=1:9:length(t2)sample5(i)=sample1(k);i=i+1;endfigure(18);stem(1:9:length(t2)/8000,sample5);% 除去相邻采样点间零点的采样信号 xlabel(t),y

37、label(y);title(8 采样信号 );%sample_junzhi8=mean(sample4)% 均值 sample_fangcha8=std(sample4)% 方差sampleunfan gzhi8=sample_fa ngcha8+sample_j un zhi8.A2%均方值%sample_xcorr8=xcorr(sample4);t3=(-Ns+1)*fs1/Fs:(Ns-1)*fs1/Fs;% 相关函数图像横坐标 figure(19);plot(t3,sample_xcorr8);% 相关函数 xlabel(t),ylabel(R);title(8 采样信号相关函数

38、);%求概率密度F2,y2=ksde nsity(sample4);%y1为输入信号所有取值，F1为每个值相应概率figure(20);plot(y2,F2);% 概率密度xlabel(y),ylabel(F);title(8 采样信号概率密度 );%求频谱 sample_spectra8=fft(sample4);f=40000*n/Ns;% 频域横坐标figure(21);plot(f(1:150),abs(sample_spectra8(1:150);% 频谱 %plot(abs(y_spectra);xlabel(f),ylabel(Y);title(8 采样信号频谱 );%求功率谱密

39、度P2=sample_spectra8.*conj(sample_spectra8)/Ns;% 频谱函数的平方求时间平均 figure(22);plot(f(1:300),abs(P2(1:300);% 功率谱密度xlabel(f),ylabel(S);title(8 采样信号功率谱密度 );%求4插值t4=zeros(1,(length(t2)-1)*4+length(t2);% 插值信号横坐标for k=1:length(t4)if mod(k,5)=1t4(k)=(1/fs1)*fix(k/5);endif mod(k,5)=2t4(k)=(1/fs1)*fix(k/5)+(1/fs1)

40、/5;endif mod(k,5)=3t4(k)=(1/fs1)*fix(k/5)+(2/fs1)/5;endif mod(k,5)=4t4(k)=(1/fs1)*fix(k/5)+(3/fs1)/5;endif mod(k,5)=0t4(k)=(1/fs1)*(k/5-1)+(4/fs1)/5;endendinter4=interp1(t2,sample1,t4,cubic);figure(23)stem(t4,inter4);% 插值信号xlabel(t),ylabel(y);title(4 插值信号 );figure(80)plot(t4,inter4);% 插值信号xlabel(t),

41、ylabel(y);title(4 插值信号 );%4插值的均值：disp(4 插值信号均值 :); inter4_mean=mean(inter4)% 均值disp(4 插值信号方差 :); inter4_var=var(inter4)% 方差disp(4 插值信号均方值 :);in ter4_rms=i nter4_var+i nter4_mea n42%均方值t5=(-Ns+1:(Fs/fs1)/5:Ns-1)/Fs;% 相关函数图像横坐标 inter4_xcorr=xcorr(inter4);figure(24);plot(t5,inter4_xcorr);% 相关函数 xlabel(

42、t),ylabel(R);title(4 插值信号相关函数 );F3为每个值相应概率F5,y5=ksdensity(inter4);%y3 为插值信号所有取值， figure(25);plot(y5,F5);% 概率密度xlabel(y),ylabel(F);title(4 插值信号概率密度 );f1=5*fs1*(0:length(t4)-1)/length(t4);%频域横坐标inter4_spectra=fft(inter4);figure(26);plot(f1(1:300),abs(inter4_spectra(1:300);%频谱xlabel(f),ylabel(Y);title(4 插值信号频谱 );P5=inter4_spectra.*conj(inter4_spectra)/length(t4);figure(27);plot(f1(1:300),P5(1:300);% 功率谱密度 xlabel(f),ylabel(S);title(4 插值信号功率谱密度 );%