《方差与协方差》ppt课件

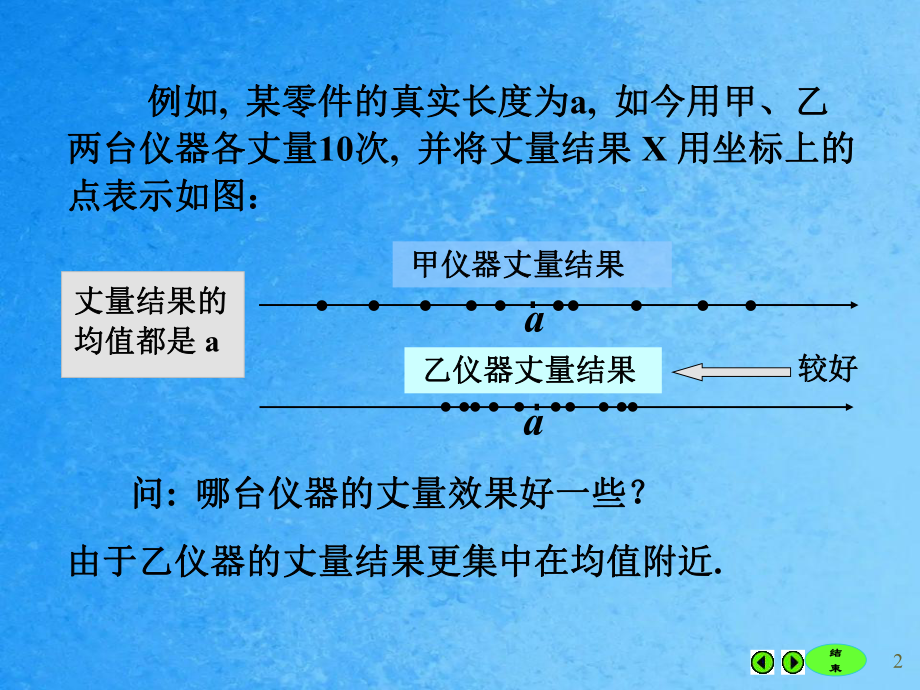
1、1结结束束 随机变量的数学期望随机变量的数学期望(均值均值), 它表达了随机它表达了随机变量取值的平均程度变量取值的平均程度, 是随机变量的一个重要的是随机变量的一个重要的数字特征数字特征. 但是在很多场所但是在很多场所, 仅仅知道平均值是不够的仅仅知道平均值是不够的. 2 随机变量的方差随机变量的方差 2结结束束 例如例如, 某零件的真实长度为某零件的真实长度为a, 如今用甲、乙如今用甲、乙两台仪器各丈量两台仪器各丈量10次次, 并将丈量结果并将丈量结果 X 用坐标上的用坐标上的点表示如图：点表示如图：问问: 哪台仪器的丈量效果好一些？哪台仪器的丈量效果好一些？ a 甲仪器丈量结果甲仪器丈量

2、结果 a 乙仪器丈量结果乙仪器丈量结果较好较好由于乙仪器的丈量结果更集中在均值附近由于乙仪器的丈量结果更集中在均值附近.丈量结果的丈量结果的均值都是均值都是 a3结结束束 为此需求引进另一个数字特征为此需求引进另一个数字特征, 用它来度量用它来度量随机变量在其中心随机变量在其中心 (即均值即均值) 附近取值的离散程度附近取值的离散程度(或集中程度或集中程度). 这个数字特征就是这个数字特征就是: 方差方差. 再如再如: 调查某车床加工轴承的质量时调查某车床加工轴承的质量时, 假设假设最关键的目的为长度最关键的目的为长度, 那么不但要留意轴承的平均那么不但要留意轴承的平均长度长度, 同时还要思索

3、轴承长度与平均长度的偏离同时还要思索轴承长度与平均长度的偏离程度程度 (即加工的精度即加工的精度); 等等等等.我们该用怎样的量去度量这种偏离程度呢我们该用怎样的量去度量这种偏离程度呢? X E(X) ? E X E(X) ? E | X E(X) | ?E X E(X) 2 4结结束束 一、方差一、方差( variance )的定义的定义随机变量随机变量 X 的平方偏向的平方偏向 X E(X) 2 的均值的均值 )(2XEXE 记作记作)(XD或或 Var ( X ) ,叫做叫做 X 的方差的方差.而而)(XD记作记作)(X X 或或 叫做叫做 X 的规范差的规范差或均方差或均方差. 方差刻

4、划了随机变量取值的离散程度方差刻划了随机变量取值的离散程度:假设假设 X 的取值比较集中的取值比较集中, 那么方差较那么方差较小；小；假设假设 X 的取值比较分散的取值比较分散, 那么方差较那么方差较大大 .5结结束束如如: : 据以往记录据以往记录, , 甲乙两射手命中环数甲乙两射手命中环数 X X、Y Y 的分布律的分布律为为 X 6 7 8 9 10P 0.1 0.2 0.4 0.2 0.1Y 6 7 8 9 10P 0.2 0.2 0.2 0.2 0.2及及可以算出可以算出:)(XE1 .0102 .094 .082 .071 .06 ,0 .8 ,0 .8)( YE两人命中环数的平均

5、程度一样两人命中环数的平均程度一样, 从中看不出两人射击技术的从中看不出两人射击技术的高低高低;但但 )()(2XEXEXD 1 . 0)2(2 2 . 0)1(2 4 . 002 2 . 012 1 . 022 ,2 .1 ,0 .2)( YD阐明甲的命中环数比乙的更集中阐明甲的命中环数比乙的更集中, ,即甲的射击技术比乙的稳定即甲的射击技术比乙的稳定. .6结结束束二二. 方差的简化计算公式方差的简化计算公式 )(XD)(2XE2)(XE 即即: 方差等于方差等于 平方的期望平方的期望 减减 期望的平方期望的平方.证明证明:)()(2XEXEXD )()(222XEXXEXE 22)()(

6、)(2)(XEXEXEXE .)()(22XEXE 7结结束束例例: 设设 X 的概率密度的概率密度为为 ., 0,10,)(其其它它xbxaxf且且 D( X ) = 1/18, 求求 a, b 及及 E( X ).而而解解:由归一性得由归一性得 xxfxXEd)()( 10d)(xbxax xxfd)( 10d)(xbxaba 2, 1令令 ,23ba xxfxXEd)()(22 102d)(xbxax34ba 故故22)()()(XEXEXD 223 baba22 36222bb ,181令令 解得解得 b = 0, a = 2, E( X ) = 2/3,34ba 或或b = 2, a

7、 = 2, E( X ) = 1/3 .8结结束束例例: :设设 (X, Y) 的概率密度为的概率密度为 ., 0, 10,8),(其其它它yxyxyxf试求试求 D( X ), D( Y ) . D( X ), D( Y ) . 解解: )(XE 101d8dxyyxxx,158 yxyxfxdd),(,31 )(2XE 1012d8dxyyxxx22)()()(XEXEXD ,22511 )(YE 101d8dxyyxyx,54 )(2YE 1012d8dxyyxyx,32 22)()()(YEYEYD .752 xy01y=x9结结束束三三. 常见分布的期望与方差常见分布的期望与方差(3

8、),2)(baXE 那那么么,),(baUX(2)那那么么,)(P X,)( XE(1)那那么么,),(pnBX,)(pnXE (4)那那么么 , )( eX,/1)( XE(5),),(2 NX那那么么 ,)( XE.)(pqnXD .)( XD.12)()(2abXD ./1)(2 XD.)(2 XD10结结束束四四. 方差的性质方差的性质(1) 对恣意常数对恣意常数 k 与与 c 有有: D( k X + c ) = k 2 D(X).(2) 设设 X 与与 Y 相互独立相互独立, 那么那么 进一步进一步, 假设假设 X1 , , Xn 相互独立相互独立, 那么对恣意那么对恣意常数常数

9、c1 , cn 有有: D(X+Y) = D(X) + D(Y), D(XY) = D(X) + D(Y). D( c1 X1+ + cn Xn ) = c12 D( X1 ) + + cn2 D( Xn ).(3) D(X) = 0 的充要条件是的充要条件是 X 以概率以概率 1 取常数取常数 C , 即即 PX = C = 1 . 11结结束束例例: :那那么么,),(pnBX,)(pnXE .)(pqnXD 解解: X 表示表示 n 重伯努利实验中重伯努利实验中 “胜利的次数胜利的次数, p为每次实验胜利的概率为每次实验胜利的概率, 那么那么 X B(n, p);引入引入 iX1, 假设

10、第假设第 i 次实验胜利次实验胜利,0, 假设第假设第 i 次实验失败次实验失败. i =1, 2, , n,那么那么 X1 , X2 , Xn 相互独立相互独立, 且且,1 niiXX而而 Xi 的分布律的分布律为为 Xi 0 1 P q p故故 E( Xi ) = p , E( Xi2 ) = p , D( Xi ) = E( Xi2 ) E( Xi )2 = p q ,从而从而 niiXEXE1)()(,np niiXDXD1)()(.npq 12结结束束例例: 有限个独立正态变量的线性组合依然服从有限个独立正态变量的线性组合依然服从正态分布正态分布, 假设假设), 2 , 1(),(2

11、niNXiii 且它们相互独立且它们相互独立, 那么那么),(12211 niiiniiiniiiccNXc 解解:)(1 niiiXcE niiiXEc1)(,1 niiic )(1 niiiXcD niiiXDc12)(.122 niiic 13结结束束五五. 随机变量的规范化随机变量的规范化 设设 X 具有具有)()(XDXEXY 为为 X 的规范化随机变量的规范化随机变量.E( Y ) = 0,D( Y ) = 1. 那么叫那么叫,)( XE,0)(2 XD X14结结束束六六. 切比雪夫切比雪夫(Chebyshev)不等式不等式 对对 X, 假设假设 E( X ), D( X ) 都

12、存在都存在, 那么那么对对2)(| )(| XDXEXP 有有0 或或.)(1| )(| 2 XDXEXP (1) 方差确实能衡量随机变量取值的离散程度方差确实能衡量随机变量取值的离散程度.(2) 该不等式能在该不等式能在 X 的分布未知的情况下对的分布未知的情况下对| )(| XEX的概率的下限作一估计的概率的下限作一估计, 假设假设记记,)( XE,)(2 XD那么那么3| XP,9/8 等等等等. 15结结束束 一、协方差一、协方差随机变量随机变量 X 和和 Y 的协方差的协方差 ),(CovYX 前面我们引见了随机变量的数学期望和方差前面我们引见了随机变量的数学期望和方差, 对于多维随

13、机变量，反映分量之间关系的数字特征对于多维随机变量，反映分量之间关系的数字特征中中, 最重要的就是协方差和相关系数最重要的就是协方差和相关系数.)()(YEYXEX E3 协方差协方差(Covariance)和相关系数和相关系数1. 定义定义:16结结束束(1) Cov( X, Y )= Cov( Y, X )(2) Cov( a X, b Y ) = a b Cov( X, Y ) , a, b 是常数是常数(3) Cov( X1 + X2 , Y )= Cov( X1 , Y ) + Cov( X2 , Y ) 2. 简单性质简单性质:3. 协方差的简化计算公式协方差的简化计算公式: Co

14、v( X, Y ) = E( X Y ) E( X ) E( Y )可见，假设可见，假设 X 与与 Y 独立独立, 那么那么 Cov( X, Y ) = 0 .4. 随机变量和的方差与协方差的关系随机变量和的方差与协方差的关系 D ( X+Y )= D( X ) + D( Y ) + 2Cov( X, Y )17结结束束二、相关系数二、相关系数1. 定义定义: 设设 D( X ) 0, D( Y ) 0, 称称)()(),(CovYDXDYXYX 为随机变量为随机变量 X 和和Y 的相关系数的相关系数.注注: 相关系数也叫规范协方差相关系数也叫规范协方差, 其实是规范化其实是规范化随机变量随机

15、变量)()(XDXEX )()(YDYEY 的协方差的协方差. YX 与与18结结束束1|)1( YX 2. 相关系数的性质相关系数的性质:1|)2( YX 存在常数存在常数a, b 使使, 1 bXaYP即即 X 和和 Y 以概率以概率 1 线性相关线性相关.可见相关系数刻划了可见相关系数刻划了 X 和和 Y 间间“线性相关的程度线性相关的程度.的值越接近于的值越接近于 1, Y 与与 X 的线性相关程度越高的线性相关程度越高;|YX |YX 的值越接近于的值越接近于 0, Y 与与 X 的线性相关程度越弱的线性相关程度越弱;那么那么 Y 与与 X 有严厉线性关有严厉线性关系系;假假设设,

16、1| YX 假假设设, 0| YX 那么那么Y 与与X 无线性关系无线性关系, 叫做叫做 X 与与Y 不相关不相关.19结结束束留意留意:假设假设 X 与与 Y 独立独立, 那么那么 Cov(X, Y) = E(XY )E(X )E(Y ) = 0, 但由但由 X 与与 Y 不相关不相关, 不一定能推出不一定能推出 X 与与 Y 独立独立.而对下述情形而对下述情形, 独立与不相关等价独立与不相关等价:假设假设 (X, Y) 服从二维正态分布服从二维正态分布, 那么那么X 与与 Y 独立独立X 与与 Y 不相关不相关.从而从而 X 与与 Y 不相关不相关; ,0)()(),(Cov YDXDYX

17、YX 20结结束束例例: 设设 X 在在 (1/2, 1/2)内服从均匀分布内服从均匀分布, 而而 Y = cos X , 试调查试调查 X 与与 Y 的相关性及独立性的相关性及独立性?解解:而而 Y 与与 X 有严厉的函数关系有严厉的函数关系,因此因此 .,0,5 .05 .0, 1)(其其它它xxfX, 0)( XE)(YE xxfxXd)(cos)(cos XE 5 . 05 . 0dcosxx,21sin2 )(YXE)cos(XXE 5 . 05 . 0dcosxxx, 0 Cov( X, Y ) = E( X Y ) E( X ) E( Y ) = 0,0)()(),(Cov YD

18、XDYXYX 故故 X 和和 Y 不相关不相关 .即即 X 和和 Y 不独立不独立 .21结结束束 一、矩一、矩为为 X 的的 k 阶原点矩阶原点矩,可见可见: X 的期望是的期望是 X 的的 1 阶原点矩阶原点矩; 在随机变量的数字特征中在随机变量的数字特征中, 更普通的是矩更普通的是矩. 4 矩、协方差矩阵矩、协方差矩阵)(kXE为为 X 的的 k 阶中心矩阶中心矩,)( kXEXE 为为 X 和和 Y 的的 k + l 阶混合原点矩阶混合原点矩, )(lkYXE 为为 X 和和 Y 的的 k + l 阶混合中心矩阶混合中心矩.)()( lkYEYXEXE X 的方差是的方差是X 的的 2 阶中心矩阶中心矩; X 和和 Y 的协方差是的协方差是 X 和和 Y 的的 2 阶混合中心矩阶混合中心矩.22结结束束二、协方差矩阵二、协方差矩阵 对对