浅谈数形结合思想的应用

1、浅谈数形结合思想的应用一、研究数形结合思想的必要性数学是研究现实lit界屮空间形式和数最关系的科汛数和形是数学屮最基本的两人概 念，也是整个数学发展过程中的两大柱石，数借助形产牛直观效果，形依赖数能深刻入微. 数和形以一定条件互相转化，数最关系借用图形的性质，使许多抽象的概念肓观化，形象化, 简单化；而图形问题在运用了数量关系的公式法则后，使较艰深的问题归结为较容易处理的 数量关系式的研究.数形结合是根据数的结构特征，通过唤起表象或通过再造想象，构造出与之相适应的 几何图形，并利用图形的特征和规律，解决数的问题，或将图形信息部分或全部转化成代数 信息，削弱或清除形的推理部分，使要解决的形的问题

2、转化为数最关系的讨论.数形结合是研究数学和数学教学中的重要思维原则之一，其解法跨越了数学各分科知 识的界限数形结合是沟通数形之间的联系，并通过这种联系所产工的感知或认知的作用， 形成和谐完关的数学概念，廿找问题解决途径的种有效方法数形结合是直观与抽象，感 知与思维的结合.数形结合思想采用了代数方法和儿何方法最好的方血：儿何图形形象直观，便于理解；代数 力法的般性，解题过程的程序化，可操作性强，数形结合的思想方法是学好中学数学的重 要思想方法.因此，研究数形结合思想是相当必要的.二、数与形在解题中的转化数学研究的対象是数量关系与儿何图形，数和形既是对立的乂是统一的，并且在一定 条件下可以相互转化

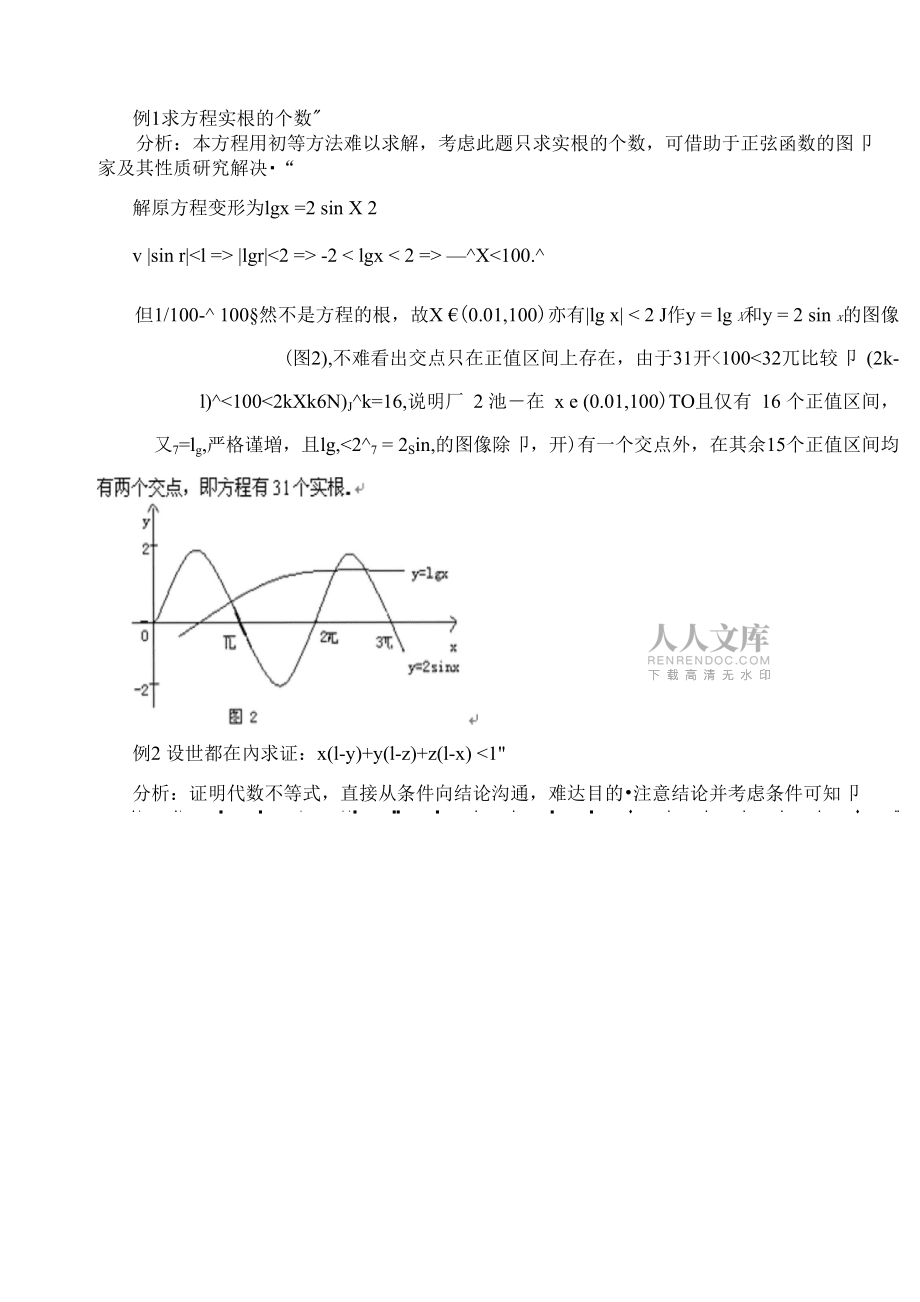
3、，结合运用数最关系可以通过图形或图像肓观的表示出来，然麻应用 几何知识形象的解答行关代数问题；另方面，冇关图形的性质可通过数最关系来描述和计 算，从而用代数方法來解决儿何问题.1.数量问题转化为图形问题有关数的问题，借用形的性质之后，有助于对问题的内在联系更进一步的了解，从而 变易错为准确，化繁琐为简捷而数最问题转化为图形问题的匸要力法是用几何力法解决代 数问题，而儿何方法具有直观，形象的优势.例1求方程实根的个数"分析：本方程用初等方法难以求解，考虑此题只求实根的个数，可借助于正弦函数的图卩 家及其性质研究解决“解原方程变形为lgx =2 sin x 2v |sin r|<l

4、 => |lgr|<2 => -2 < lgx < 2 => x<100.但1/100- 100§然不是方程的根，故x (0.01,100)亦有|lg x| < 2 j作y = lg x和y = 2 sin x的图像 (图2),不难看出交点只在正值区间上存在，由于31开<100<32兀比较卩 (2k-l)<100<2kxk6n)jk=16,说明厂 2 池在 x e (0.01,100)to且仅有 16 个正值区间， 又7=lg,严格谨増，且lg,<27 = 2sin,的图像除卩，开)有一个交点外，在其余15

5、个正值区间均例2 设世都在內求证：x(l-y)+y(l-z)+z(l-x) <1"分析：证明代数不等式，直接从条件向结论沟通，难达目的注意结论并考虑条件可知卩 &1-心1-儿1-2均为正数，且似两线段积之和，联想三角形面积公式s=-ab sin g构造三角形从而将数量间题转化为图形间题2证明 构造辺长为1的等辺三角形abc,在少老上各取菽得ap =心“bq = z, ce =厂则 bp = 1 - cq = 1 - z, ae = 1 - ”，由图孑知： 轧观 + 沐嗣 +，则知不等式成立3图3a例3已知”一舖一»|=1,求使国最大的复数z“分析：本题为最大值

6、间题，可设£=兀+ 代入已知等式中，把它转化为一般求最值的间3题，但过程比较鑿难，现结合复数的几何意义进行讨论2解 满足条件|z-5-jj|=l的z在复平面上杲以（甩-1）为圆心，1为半径的圆上的点a（图4）,按要求在这些z中找出模最大的一个，即到原点距离最远的一个显然，过原点。和圆心c作直线 交圆于则叼的模数为最大：于杲知叼为所求，即z= 亚丄i模数最大22 22 图形间题转化为数量间题a有些平面几何，立体几何间题若利用代数方法去解决，其解题方法变得容易寻找，解题过程也变得简单因此化形为数，解题思路较明确，规律性较强2例4已知正方体遊q,延长至e, ce = -bc,在cd上截取d

7、f = -dc , de与心23肿的延长线交于g,则g在正方形肋cq的外接圆上（图5）2分析：这是一个图形间题，如何创造条件将它转化为数壘间题呢？对图形进行壘化是将3 图形i可题转化为数量i可题的关键本题为五点共圆i可题，由于as爼是正方形，故只须证g在d所 在的區1上，亦可证a, c, g, d四点共圆.2迄阴 连接在三旁弓加p丰悵疼正弦走倉.令屈之.， ap则smcaf = -.在rtg 丰.smcds= = - tzcaf 2z0龙 巻为渗.5db 5.zcaf = zcde总ac,g,d四点吴圆即g在王方殄個外冬回上.例5 abcd的爲主朋cdz.和弓于一蚕方c矣一蛍肋的中点为e求辽:

8、 加丄分折：引入平盘言楚坐标罢.刮至熒折迭即可待三， 证明 取坐标系如图6设班o),bs，o),c(0,c),d(d,c),则'ev | + | - | ' a+(-d)= j(2+c d = a +0 -q(q +c$c- -02r r =2_ _2=!：=_ig "b-±±-a(p-ay-(a-by-c因为数量关系转化为图形问题的条件是将数量问题图形化，图形问题转化为数量 问题的条件是对图形问题进行量化，所以研究数量问题的图形化与对图形问题进行量化对提 高解题能力是相当有必要的同时在数学解题屮若能很好的根据问题的特点和需要，由数思 形，以形助数

9、，适时转化，相互作用，能使我们解题思路开阔，解题敏捷.三、数形结合思想在解题中的优越性数形结合是数学中一种重耍思想方法，也是高考要考查的重点思想方法z,数形结 合以解题的直观，形象，简洁著称，下而从几方而谈谈其在屮学数学解题屮的优越性.1.简洁性lg（2,）例1若方程 一 =2有实数解，求实数住的取值范围21附-0）分析：此题是一个含参数的对数方程若按方程思想来加以解决，那必须首先要注意函数的定义域，而 吕利用一元二次方程根的分步思想来加以解决，需要进行分类讨论，过程较堅琐，若能转变思路，利用函i 更的图像，那么间题可以简洁的加以解决.卩白原方程可得：，bp lg2- x2 j = lg（x-

10、 <7）,那么2-只=（x-a）,令yx - 2 - x2 ,y2 = x-a f :j壬同一坐标系中作出函数的图像，如图1,此时，实数口的意义就是直线y2=x-a在卩轴上的截距，由图 y知：当2wqw庞时两曲线有交点，又因兀-qhi,令兀=。+1代入原方程得：.越& = -2,所以： 口工一2,所以，实数说的取值范围是:（-2,0）u（0,v2）.,图72.奇异性a例2已知等差数列%中，前”项之和为若0二显伽h勿，求s”的值*分析：这是数列中的一个典型间题，可利用数列的不同方法来加以解决，此处若能充分"理解数列的函数属性，利用函数图像来加以解决，那真是有神来之笙！充分

11、体现了数学中的奇异性在数列 的学习中,我们知道等差数列前”项之和瓦是关于"的二次函数，且常数项为0,因为耳=©时,点（比）3 突破性3例3试判断方程八+ 1八+2x+2a （° > o且°工1）的解的个数*分析：这是我们经常能见到的一种题目的类型，要解出方程是不可能的，但是题目只要心龙们判断方程解的个数，我们若能突破传统的解方程思想，转而利用图形的观点来处理，那么这类间题的: 律決:将变的轻而易举，方程+1=-八+2尤+2.且仪工1）的解的个数，实质上杲尹=/和: 卩2 = -” + 2兀-1 + 2幺图像交点的个数，分别作出a >1和0<a<l的图像，如图9,易得两曲线有两个交上面一个方面是数形结合的二要优越性，在解决问题时，我们要多注意发挥图像的功 能，帮助我们开拓思路，辅助我们解决问题.四、总述综观中学数学，可以知道其研究的对彖不外是一些常见的数量关系与简单的图形，数 与形不仅是两个相互对立的概念，而口是数学中较其他对立较为特殊的一种对立，然而，数 与形与其他对立的双方一样，也可以在一定的条件下实现相互转化.华罗庚曾说