外文翻译译文-用概率的方法去预测疲劳裂纹萌生.docx
典型机翼机身对接结构CATIA三维建模【含CAD图纸、说明书】
收藏
资源目录

压缩包内文档预览:
编号:22906594
类型:共享资源
大小:2.49MB
格式:ZIP
上传时间:2019-11-04
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
含CAD图纸、说明书
典型
机翼
机身
对接
结构
CATIA
三维
建模
CAD
图纸
说明书
- 资源描述:
-
【温馨提示】压缩包内含CAD图有下方大图片预览,下拉即可直观呈现眼前查看、尽收眼底纵观。打包内容里dwg后缀的文件为CAD图,可编辑,无水印,高清图,压缩包内文档可直接点开预览,需要原稿请自助充值下载,所见才能所得,请见压缩包内的文件及下方预览,请细心查看有疑问可以咨询QQ:11970985或197216396

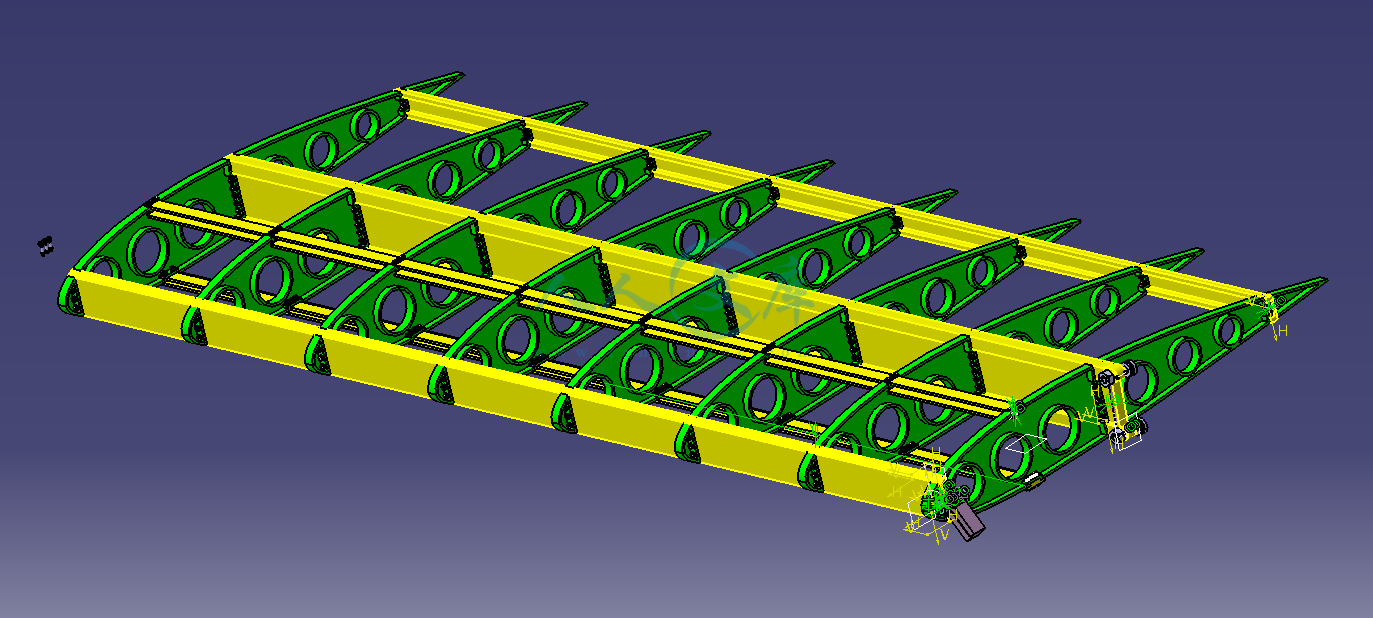
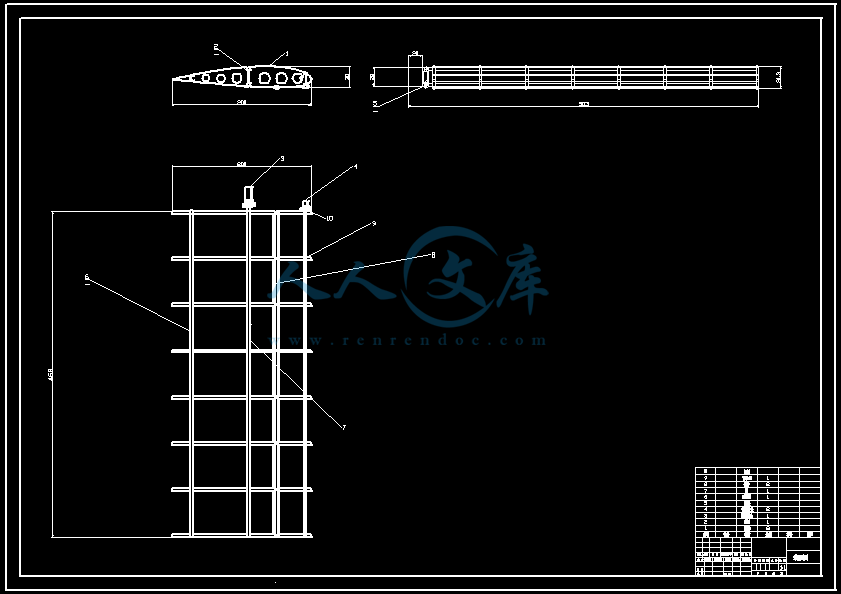




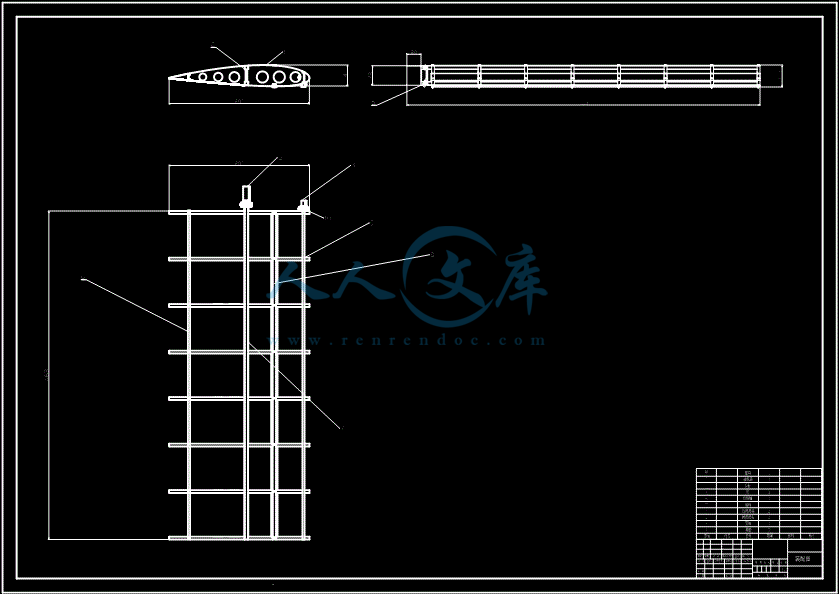



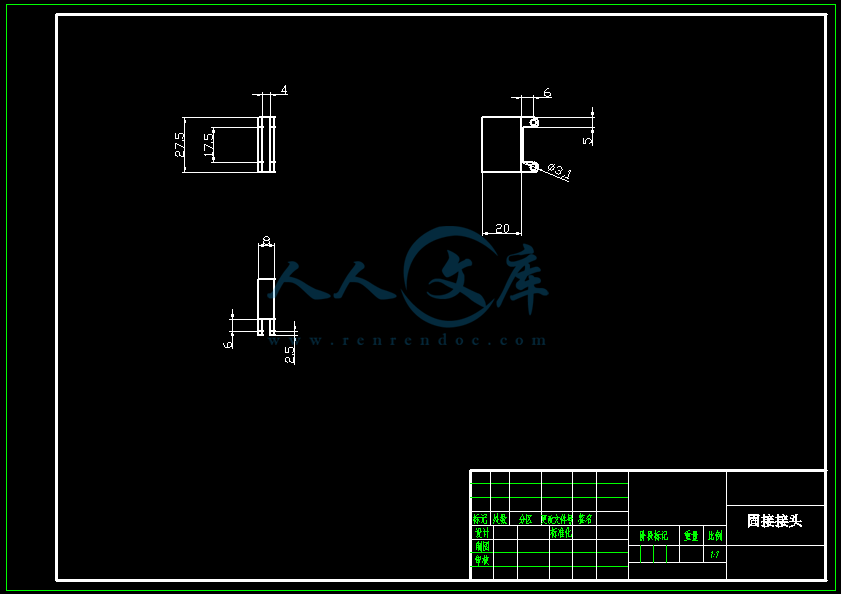
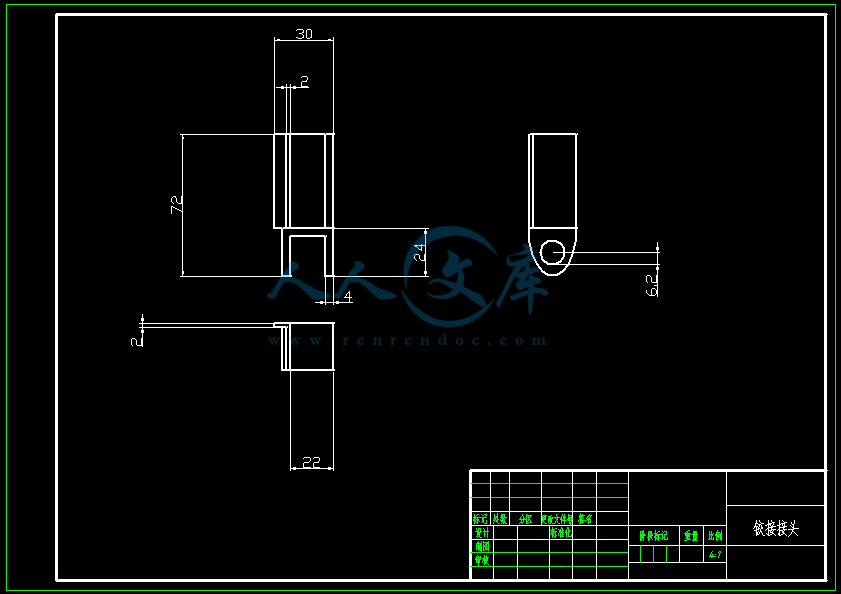

















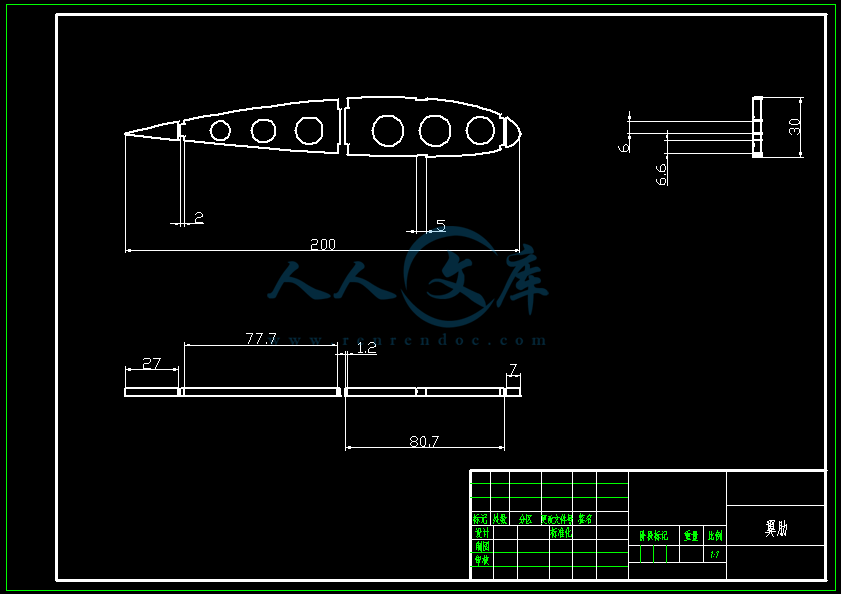
- 内容简介:
-
毕 业 设 计(论 文)外 文 参 考 资 料 及 译 文译文题目: A probabilistic method to predict fatigue crack initiation用概率的方法去预测疲劳裂纹萌生 学生姓名: 学 号: 专 业: 所在学院: 指导教师: 职 称: 20xx年 2月 27日用概率的方法去预测疲劳裂纹萌生摘要:在这篇文章,提出了疲劳损伤,所以可以用一种概率的方法去预测宏观裂纹萌生。声学非线性用来量化宏观裂纹萌生。这些数据被用来概率分析裂纹损伤。这种概率裂纹损伤分析包括合理选择损伤破坏模型和计算裂纹萌生概率的步骤。它评估靠重要性采样的蒙特卡洛方法。模拟裂纹损伤的概率性被提出,并且与实际实验结果做比较。关键字:声学非线性,裂纹萌生,损伤演变,疲劳,概率性方法,结构安全监测1、 介绍 传统的部件使用寿命预测是依赖于安全法则和线性积累的Palmgren和Miner法则。在金属损伤的安全法则里,使用寿命预测是基于疲劳试验的数据里。当失效的可能性达到一个规定的值,即使一些部件还有运用的价值和意义,一种结构(房屋)的部件也要被替代。因此,经济处罚是一个保守的做法。为了避免这种刑罚,“破坏宽容”的做法往往是一个合适的替代寿命预测方法。这种方法是特别有用的,当损失率的积累是很好的理解,并可以监测用定量无损评价技术。然而,在某些材料,如高强度钢,如那些用于旋翼机的传动系统,在裂纹检测的临界损伤但非常小的长度,通常发生在一个组件的寿命末期。当一个可检测的裂纹已经发展出的微观损伤过程,它生长到一个不可接受的长度,与组件的总寿命相比是一个短的时间。用周期性的监测系统的监控,但是,显着提高了安全性的损伤容限的方法。特别是,如果预裂纹损伤可以监测和相关的裂纹形成的分析性疲劳损伤过程,可以得到大量的安全和成本效益。有了这个目标,计算方法基于原位测量周期宏观裂纹萌生的几率是本文提出的。该方法基本上由两个部分组成:一种结构寿命监测系统监测疲劳过程。在本方法中,声学二次谐波产生(见2节)是用来监测疲劳过程中积累的损害。 概率疲劳损伤过程,将数据从寿命监测系统输入,计算裂纹萌生的概率作为输出。概率损伤过程包括选择一个合适的损伤演化方程模型的累积损伤(见3节)和一个程序计算宏观裂纹萌生的概率(见4节)。程序计算裂纹萌生的几率是能够更新基于最新的检测数据,监测系统预测。使用这种方法,宏观裂纹萌生的概率计算为来源于文献,并且结果在第5节。2. 声二次谐波发生 在一个组件进行疲劳的过程要量化损伤的积累,最重要的可观察的变量是损伤积累。在试样中,所累积的损害是由引入材料非线性组成部分的微观结构的变化引起的。为了表征材料的非线性特性,由换能器(发生器)所产生的一个单一的频率的超声波的发送通过试样和接收换能器接收的信号进行了分析。材料的非线性失真,使单频波形失真,导致二次谐波和高次谐波的产生。其结果是,接收到的信号的接收器不仅包括在发送(基波)的频率,但也二次和高次谐波的振幅增加作为材料的非线性增加的一个组件。因此,材料非线性和潜在的累积损伤的特征可以通过对二次谐波的振幅A2的A1的振幅比。这比率以后称为A2、A1和预计将增加累积损伤的进展。注意,A2/A1的声学非线性特性(见奥吉等人,2001)用在这里是不同于通常在文献中找到(例如见莫里斯等人,1979)。 奥吉等人(2001)用电磁声换能器测量A2/A1在试样进行疲劳。相对于程序之前描述的测量比A2/A1发送一个简单(基本)频率波和测量频率波的基波和二次谐波信号的幅值,奥吉和他的同事用了一个不同但类似的程序。他们分别发送的两个不同的信号,一个在共振频率fr和另一个频率fr / 2,制成标本。当信号在频率fr传送时,他们测量与频率fr的接收信号的振幅为A1(FR)。当信号传输频率fr / 2他们测量与频率fr表示A2接收信号的振幅(FR / 2)。观察A2(FR / 2)是二次谐波的振幅。注意,本程序可以确保测量换能器的共振频率fr都测量信号,从而更准确的测量。详细信息请参阅奥吉等人(2001)。他们观察到比A2(FR / 2)/ A1(FR)增加近单调,并显示在宏观裂纹起始点不同的峰值(见图1)。 这表明,在疲劳在试件破坏的状态可以通过测量比A2/A1不同周期数的跟踪。3.破坏模型 本节介绍了损伤模型,它的演化是比率A2(FR / 2)/ A1(FR)(见2节)到宏观裂纹起始点。在一个特定的周期在疲劳过程中的损伤的状态表示由一个标量损伤函数D(N),其中N是周期数。大小D = 0对应于无损伤,D = 1对应于第一裂纹的出现。假设下面的模型代表的损伤的演化的周期数。 在这里,数控是归一化常数,在循环应力范围,RC()耐力极限时,在一个周期的平均应力,m0,n0,取决于材料和载荷条件,通过相关联的比A2/A1演变至D.进化假定RC参数的确定()如下古德曼关系(见Goodman,1899).rc() =rc(0)(1 /ult)ULT是材料的极限抗拉强度。假设和不断循环,/ 2总是大于混凝土中(),方程(1)可以写成D(N)= 1 (1D0)n+1 (N-N0)/ N c (/2 rc()/2) m(n+ 1)1/n+1在周期D0里,N0代表试样中存在的损害。4、宏观裂纹萌生几率 本节描述的宏观裂纹萌生的概率计算程序和模型的基础上,在3节中描述的。首先,一些出现在方程(2)的数量作为随机变量。宏观裂纹萌生Pma的概率,即,裂纹萌生周期数的概率,将小于指定的周期数NS,由下式给出Pma = 1Pr(D(Ns) 1) (3)根据公式1D(Ns)0从以前的方程,它是观察到的D(Ns) 1等于NsNini值得注意的是,在一个纯粹的确定性设置,妮妮对应的周期,宏观裂纹出现。这可以看出,通过设置D=1的方程(2)和求解N。因此宏观裂纹萌生的概率可以计算为Pma = 1Pr(D(Ns) 1)= 1Pr(Ns Nini)=Pr(Nini Ns) (5)计算Pma由方程(5),首先定义了一个极限状态面g =Nini Ns也让X = x1 x2xk T表示随机变量在方程(2)(例如,在本论文中,我们考虑与已知的恒定应力循环振幅问题而大量钢筋混凝土(),D0,m和n是已知概率分布的随机。然后我们有X = x1 x2 x3 x4 = Rc()m n D0)T。观查到 (6) 在FX(x)表示x的联合概率分布评价中出现的积分方程(6),随机变量映射通过Rosenblatt变换(见Rosenblatt,1952)为标准高斯空间里的随机变量,记为U = U1 U2。.英国是独立的,通常分布,具有零均值和单位标准差。修正-林德,拉克维茨-Fiessler(hl-rf)算法模型和刘描述(1989)用于获取点靠近原点的U表面上G(u)= 0。在修改后的hl-rf算法一调整步长,在每一次迭代过程中的价值函数,基于一阶最优性条件获得足够的减少。蒙特卡洛和重要性采样的采样密度为中心的整合,在你(见藤田和的,1988)是用来计算方程的积分(6)。5.样品问题 为了验证本文提出的思想的应用,宏观裂纹萌生的概率计算为一个样本问题。数据,即比A2/A1的周期数作为一个功能,就是从奥吉等人得到的。(2001)。奥吉和他的合作者进行旋转弯曲在0.25% C和一四点弯曲结构疲劳试验(质量)钢和获得比A2/A1随循环次数的变化(见图1)。材料的屈服强度为333兆帕试样,它的最大弯曲应力为280兆帕。在零平均应力,钢筋混凝土(0),材料的耐久极限,被假定为180兆帕。 模拟检查过程中,A2/A1得到图1不同周期数的周期越来越短的时间间隔。表1显示了比A2/A1测量作为一个函数的周期数(见图1)。它是观察到的比A2/A1演变中的疲劳初期不严格单调。“原始”的损伤是通过归一化非线性测量的非线性,对于给定的问题被认为是3.25103预期最高值(见图1)。“原始”的破坏是列在表2的第三列。注意要与假定的单调的损伤演化相一致(见3节),“原始”的伤害修正列作为修正的损伤在表2第四列。 这些伤害值是基于奥吉等人的实验结果(2001)。本文采用两个不同的目的。在第一个地方,他们被用来确定参数的统计数据,在方程(1)(见3)(见第)。其次,他们解释为损害测量输入到程序计算宏观裂纹萌生的概率结构健康监测系统获得的(见4节)。5.1 优先信息 计算使用前面介绍的实验数据宏观裂纹萌生的概率,假定先验信息有关的参数m和n是可用的。这是一个合理的假设,如果在实验室中进行适当的实验。在这种情况下,M和N的统计可以损伤模型的拟合计算,使用非线性回归实验数据(如德雷珀和史密斯1998)。注意到,在目前的情况下,只有一个实验数据集(Dinspj,J = 0,6)可用。要计算的统计数据,需要产生额外的数据集。额外的数据集生成的假设检验周期Ninspj,该纠正的损害有截断正态分布范围在(0,1)与母正态分布等于dinspj和标准差等于0.1的意思,即f (D0)= (D0)/)/ (1 )/ ) (1 )/ ) 0D0 4节描述。对于正在考虑的问题,它是假定,NC固定数量而RC(0),D、M和N是随机变量。固定数量的,和NC,都有相同的值,用于非线性回归(见5.1节)。被假定为具有对数正态分布的随机变量的钢筋混凝土(0分布的平均为180兆帕和5.4兆帕的标准偏差。在周期Ninspj随机变量D0是假设在区间有一个截断正态分布(0,1)与平均值和标准偏差等于0.1 Ninspj。这种分布的D0与一用于产生M的统计和N相一致(见5.1节)。被假定为有一个联合对数正态分布的统计在5.1节中给出的随机变量。从第三检查记录、宏观裂纹起始计算不同周期的概率是表3中给出的。从表3看出,概率疲劳损伤分析程序更新连续检查裂纹起始概率。对于检查裂纹萌生的累积概率分布图2。数字(1,。.图6)在图中注明检验记录的周期数。观察后立即检查,宏观裂纹萌生降到零的概率。这是由于这样的事实,
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
|
2:不支持迅雷下载,请使用浏览器下载
3:不支持QQ浏览器下载,请用其他浏览器
4:下载后的文档和图纸-无水印
5:文档经过压缩,下载后原文更清晰
|
 川公网安备: 51019002004831号
川公网安备: 51019002004831号