外文原文-用概率的方法去预测疲劳裂纹萌生.docx
典型机翼机身对接结构CATIA三维建模【含CAD图纸、说明书】
收藏
资源目录

压缩包内文档预览:
编号:22906594
类型:共享资源
大小:2.49MB
格式:ZIP
上传时间:2019-11-04
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
含CAD图纸、说明书
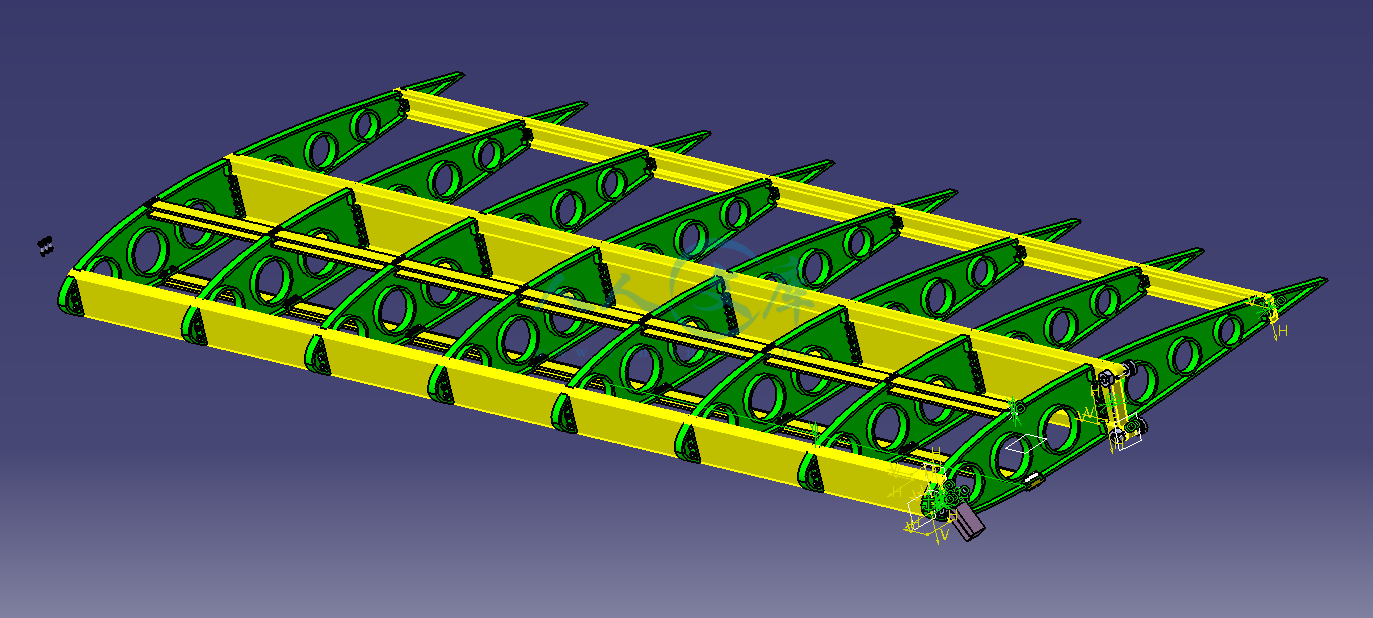
典型
机翼
机身
对接
结构
CATIA
三维
建模
CAD
图纸
说明书
- 资源描述:
-
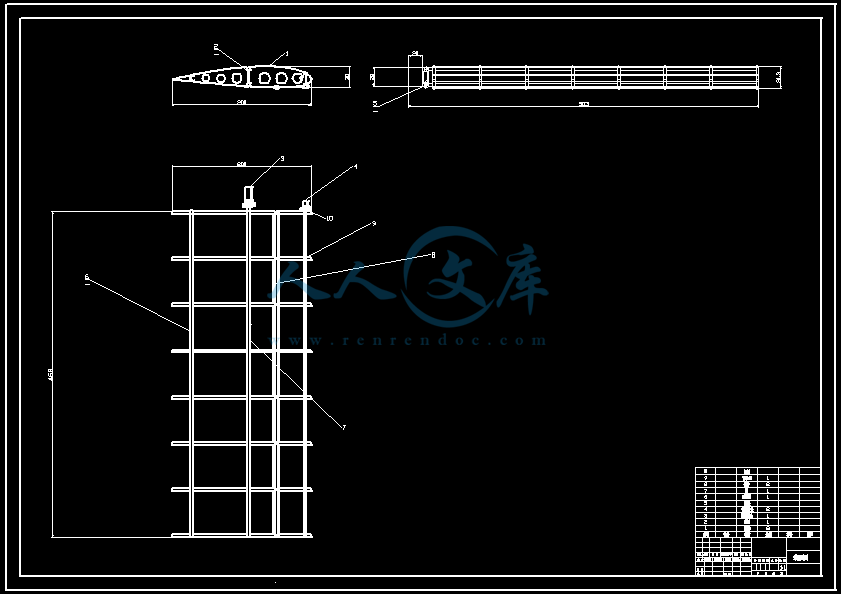
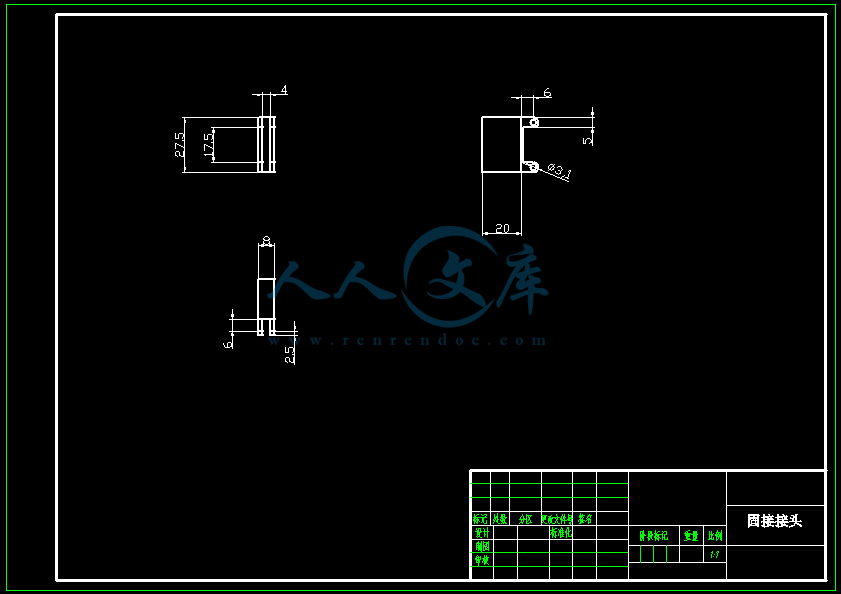
【温馨提示】压缩包内含CAD图有下方大图片预览,下拉即可直观呈现眼前查看、尽收眼底纵观。打包内容里dwg后缀的文件为CAD图,可编辑,无水印,高清图,压缩包内文档可直接点开预览,需要原稿请自助充值下载,所见才能所得,请见压缩包内的文件及下方预览,请细心查看有疑问可以咨询QQ:11970985或197216396









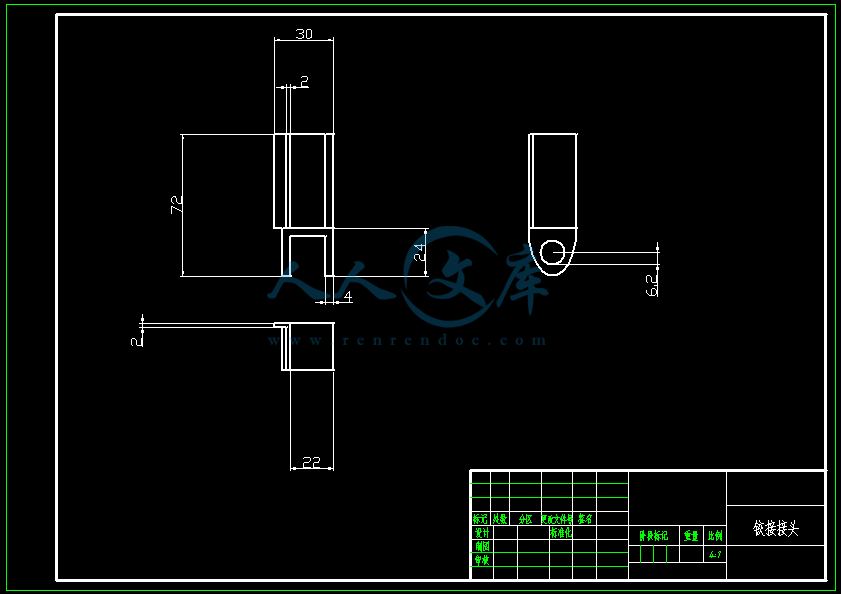

















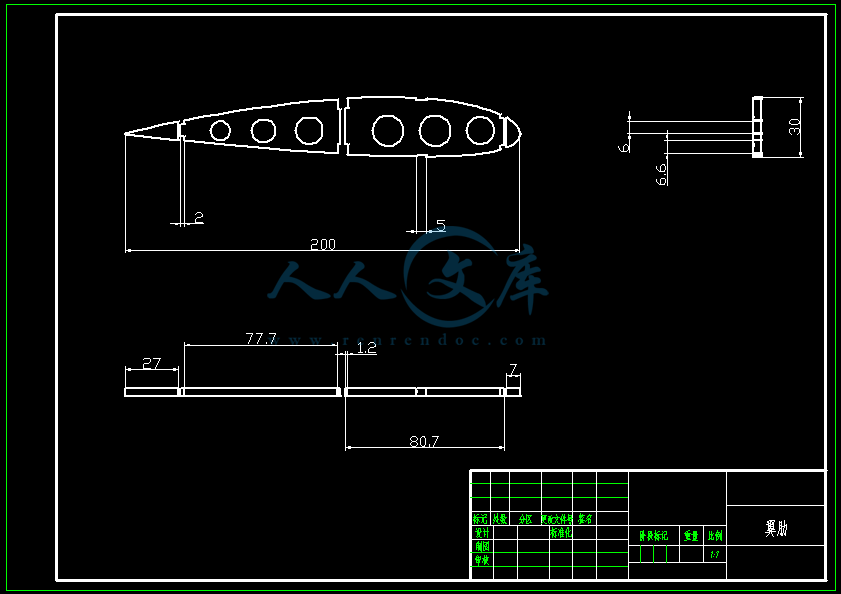
- 内容简介:
-
A probabilistic method to predict fatigue crack initiationSALIL. S. KULKARNI, L. SUN, B. MORAN, S. KRISHNASWAMY andJ.D. ACHENBACHDepartment of Mechanical Engineering, Northwestern University, Evanston, IL-60208, USAAuthor for Correspondence. (E-mail: )Received 8 August 2005; accepted in revised form 6 September 2005Abstract. A probabilistic method to predict macrocrack initiation due to fatigue damage is presented in this paper. Acoustic non-linearity is used to quantify pre-macrocrack initiation damage. This data is then used in a probabilistic analysis of fatigue damage. The probabilistic fatigue damage analy- sis consists of a suitably chosen damage evolution equation to model accumulated damage coupled with a procedure to calculate the probability of macrocrack initiation. The probability of macrocrack initiation is evaluated using the Monte Carlo Method with Importance Sampling. Numerical results for the probabilistic assessment of fatigue damage for a sample problem are presented and compared with experimental results.Key words: Acoustic non-linearity, crack initiation, damage evolution, fatigue, probabilistic method, struc- tural health monitoring.1. IntroductionConventional procedures for life prediction of components subjected to fatigue are generally based on the safe-life approach (see e.g. Suresh, 1991), coupled with Palmgren (see Palmgren, 1924) and Miner (see Miner, 1945) rules of linear cumu- lative damage. In the safe-life approach for metal fatigue, life prediction is based on data from fatigue testing of components. Components of a structure are replaced when the probability of failure reaches a prescribed (often small) value, even though some of them may have a signicant remaining life. Hence it is a conservative approach with an economic penalty. To avoid this penalty, the damage-tolerant approach is often a suitable alternative for life predictions. This approach is espe- cially useful when the rate of damage accumulated is well understood and can be monitored with a technique of quantitative non-destructive evaluation. However, in certain materials, such as high strength steels, like those used for drive trains of rotor- craft, critical damage in the form of a crack of detectable but very small length, often occurs late in the lifetime of a component. When a detectable crack has developed out of microscopic damage processes, it grows to an unacceptable length in a time that is short as compared to the total lifetime of the component. Periodic monitor- ing by a condition monitoring system can, however, signicantly improve the safety of the damage tolerance approach. Particularly, if pre-crack damage can be moni- tored and related to crack formation by an analytical fatigue damage procedure, sub- stantial safety and cost benets can be gained. With this objective, a methodology toProbabilistic method to predict fatigue crack initiation 17calculate the probability of macrocrack initiation based on periodic in situ measure- ments is presented in this paper. The methodology essentially consists of two parts: A structural health monitoring system to monitor the fatigue process. In the pres-ent approach, acoustic second harmonic generation (see Section 2) is used to mon- itor the damage accumulated during the fatigue process. A probabilistic fatigue damage procedure which takes the data from the healthmonitoring system as its input and calculates the probability of macrocrack initia- tion as its output. The probabilistic damage procedure consists of a suitably cho- sen damage evolution equation to model accumulated damage (see Section 3) and a procedure to calculate the probability of macrocrack initiation (see Section 4). The procedure to calculate the probability of macrocrack initiation is capable of updating its forecast based on the latest inspection data from the monitoring sys- tem.Using this methodology, the probability of macrocrack initiation is calculated for a sample problem taken from the literature, and the results are presented in Section 5.2. Acoustic second harmonic generationTo quantify the damage accumulation in a component undergoing fatigue, it is rst necessary to relate the accumulated damage to an observable variable. The accumu- lated damage is caused by changes in the microstructure of the component which in turn introduce material non-linearity in the specimen. To characterize the material non-linearity, a single frequency ultrasonic wave generated by a transducer (gener- ator) is transmitted through the specimen and the signal received by the receiving transducer is analyzed. The material non-linearity distorts the single frequency wave and leads to generation of second and higher harmonics. As a result, the signal received at the receiver not only consists of a component at the transmitting (funda- mental) frequency but also second and higher harmonics whose amplitudes increase as the material non-linearity increases. Therefore, the material non-linearity and the underlying accumulated damage can be characterized by the ratio of the amplitude of the second harmonic A2 to the amplitude of the fundamental A1. This ratio is henceforth referred to as A2/A1 and is expected to increase as damage accumulation progresses. Note that the characterization of the acoustic non-linearity by A2/A1 (see Ogi et al., 2001) used here is different from the one usually found in the literature (see e.g. Moris et al., 1979).Ogi et al. (2001) have used an electromagnetic acoustic transducer to measure A2/A1 in a specimen undergoing fatigue. As opposed to the procedure described ear- lier to measure the ratio A2/A1 transmit a single (fundamental) frequency wave and measure the signal amplitude at the fundamental and the second harmonic, Ogi and his co-workers used a different but analogous procedure. They transmitted two differ- ent signals separately, one at resonance frequency fr and the other at frequency fr/2, into the specimen. For the case when the signal was transmitted at frequency fr, they measured the amplitude of the component of the received signal with frequency fr denoted A1(fr). For the case when the signal was transmitted at frequency fr/2 they measured the amplitude of the component of the received signal with frequency fr denoted by A2(fr/2). Observe that A2(fr/2) is the amplitude of the second harmonic. Note that this procedure ensures that both the measured signals are measured at=Figure 1. Typical evolution of the ratio A2(fr/2)/A1(fr) for 0.25 mass % C steel, Nf 56,000 (from Ogi et al., 2001).the transducer resonance frequency fr, leading to more accurate measurements. For more details refer to Ogi et al. (2001). They observed that the ratio A2(fr/2)/A1(fr) increases nearly monotonically, and shows a distinct peak at the point of macrocrack initiation (see Figure 1).This suggests that the state of damage in a specimen during fatigue can be tracked by measuring the ratio A2/A1 for different cycle numbers.3. Damage model=This section presents a damage model whose evolution represents the evolution of the ratio A2(fr/2)/A1(fr) (see Section 2) up to the point of macrocrack initiation. The state of damage in a specimen at a particular cycle during fatigue is represented by a scalar damage function D(N), where N is the number of cycles. The magnitude D 0 corresponds to no damage, and D 1 corresponds to the appearance of the rst mac- rocrack. The following phenomenological model is assumed to represent the evolu- tion of the damage with the number of cycles 1 . O/2 rc( ) m 1dDdN =NcO/2(1 D)nif O/2 rc( ) 0if O/2 0 and n 0 are param- eters which depend on the material and the loading conditions and are determined by correlating the evolution of the ratio A2/A1 to the evolution of D. It is assumed that rc( ) follows the Goodman relation (see Goodman, 1899), i.e.ultrc( ) = rc(0) .1 where ult is the ultimate tensile strength of the material. Assuming that O and are constant during cycling and that O/2 is always greater than rc( ), Equation (1)can be solved to obtainD(N) = 1 (1 D0)n+1 N N0 . O/2 rc( ) mNcO/2 1 .(2)n+1(n + 1)Here D0 is the damage present in the specimen at cycle N0.4. Probability of macrocrack initiationThis section describes the procedure for calculation of the probability of macrocrack initiation and is based on the model described in Section 3. To begin, some of the quantities appearing in Equation (2) are taken as random variables. The probability of macrocrack initiation Pma, which is dened as the probability that the number of cycles to macrocrack initiation, will be less than a specied number of cycles Ns, is then given byPma = 1 P r(D(Ns) 1).(3)From Equation (1), it follows thatD(Ns) 0.NcO/2From the previous equation it is observed that D(Ns) 1 is equivalent toNs Nini(4).whereNini = N0 + Nc n + 1(1 D0)n+1 O/2m.O/2 rc( ) =Note that in a purely deterministic setting, Nini corresponds to the cycle at which a macrocrack appears. This can be seen by setting D 1 in Equation (2) and solving for N .The probability of macrocrack initiation can therefore be calculated asPma = 1 P r(D(Ns) 1)= 1 Pr(Ns Nini)= Pr(Nini Ns).(5)To calculate Pma given by Equation (5), one rst denes a limit state surfaceg = Nini Ns.=Also let XX1 X2 . XkT denote the random quantities in Equation (2) (for example, in the present paper we consider a problem with known constant stress 0: safe domainThe probability of macrocrack initiation Pma is therefore given byPma =g(x)0fx(x)dx,(6)=where fX(x) denotes the joint probability distribution of X. To evaluate the integrals appearing in Equation (6), the random variables are rst mapped via a Rosenblatt transformation (see Rosenblatt, 1952) into a standard Gaussian space where the random variables denoted by U U1 U2 . UkT are independent, normally distrib- uted and have zero mean and unit standard deviation. The modied Hasofer-Lind, Rackwitz-Fiessler (HL-RF) algorithm described in Kiureghian and Liu (1989) is used to obtain the point closest to the origin u on the surface g(u) 0. In the modi- ed HL-RF algorithm, one adjusts the step size during each iteration to obtain a sufcient decrease in the merit function which is based on the rst-order optimal- ity conditions. Monte Carlo integration with importance sampling, with the sampling density centered at u (see Fujita and Rackwitz, 1988) is then used to calculate the integrals in Equation (6).5. Sample problemTo demonstrate the application of the ideas presented in the paper, the probability of macrocrack initiation is calculated for a sample problem. The data, i.e. the ratio A2/A1 as a function of the number of cycles, is obtained from Ogi et al. (2001). Ogi and his co-authors have performed a rotating bending fatigue test with a four point bending conguration on a 0.25% C (mass) steel and have obtained the variation of the ratio A2/A1 with the number of cycles (see Figure 1). The yield strength of the material is 333 MPa specimen and it is subjected to a maximum bending stress of 280 MPa. The endurance limit of the material at zero mean stress, rc(0), is assumed to be 180 MPa.To simulate the inspection process, A2/A1 is obtained from Figure 1 at different number of cycles with the interval between the cycles getting progressively shorter. Table 1 shows the ratio A2/A1 measured as a function of number of cycles (see Figure 1).It is observed that the evolution of the ratio A2/A1 is not strictly monotonic dur- ing the initial stages of fatigue. The raw damage is obtained by normalizing the non- linearity measurements by the expected maximum value of the non-linearity which for the given problem is assumed to be 3.25 103 (see Figure 1). The raw dam- age is tabulated in the third column in Table 2. Note that to be consistent with the assumed monotonic damage evolution (see Section 3), the raw damage is corrected and tabulated as corrected damage in the fourth column in Table 2.Table 1. Measured values of the ratio A2/A1 during successive inspections.jNinspj(A2/A1)j 103000.901112000.802224000.903268801.504308002.005330402.506340003.10Table 2. Raw and corrected values of damage during suc- cessive inspections.jNinspjRaw damageCorrected damage Dinspj000.280.281112000.250.282224000.280.283268800.460.464308000.620.625330400.770.776340000.950.95These damage values which are based on the experimental results of Ogi et al. (2001) are used for two different purposes in the paper. In the rst place, they are used to determine the statistics of parameters m and n in Equation (1) (see Section 3). Secondly, they are interpreted as damage measurements obtained by structural health monitoring system for input to the procedure to calculate the probability of macrocrack initiation (see Section 4).5.1. Prior information=For calculating the probability of macrocrack initiation using the experimental data presented earlier, it is assumed that prior information regarding the parameters m and n is available. This is a reasonable assumption if appropriate experiments have been performed in the laboratory. In that case, the statistics for m and n can be cal- culated by tting the damage model to the experimental datasets using non-linear regression (see e.g. Draper and Smith 1998). Notice that in the present case, only one experimental data set (Dinspj ,j 0,. , 6) is available. To calculate the statis- tics for m and n additional datasets need to be generated. The additional datasets are generated by assuming that at inspection cycle Ninspj , the corrected damage has a truncated normal distribution in the range (0, 1) with mean of the parent normaldistribution equal to Dinspj and standard deviation equal to 0.1, i.e. D0 =f (D0)8 . 1 8. 0 0 D0 1=with Dinspj and 0.1. Here and 8 are the probability density and the cumu- lative distribution function of for the normal distribution. The damage model is tted to each of the additional datasets, i.e. m and n are calculated for each of the datasets. The statistics of m and n are then compiled. For the current problem, the simulations suggest that m and n are dependent parameters with means 2.9074 and 2.2295 respec- tively and the coefcient of correlation equal to 0.9029. The standard deviations of m and n are found to be 0.5336 and 0.7129, respectively.For calculating m and n using non-linear regression, the following values are used:O = 2280 MPa, = 0 MPa, Nc = 10, 000 and rc(0) = 180 MPa. The value of Nc,which is a normalizing constant is assumed to be of the order of the number of cycles to failure. For this particular problem, failure is observed at 56,000 cycles. Here Nc is taken to be 10,000.5.2. Calculation of probability of macrocrack initiationThe probability of macrocrack initiation is now calculated using the data given in Table 2. The procedure essentially consists of recording the inspection data at, say, cycle Ninspj and then calculating the corresponding value of the damage, say, Dinspj . If Dinspj Ninspj as described in Section 4.For the problem under consideration, it is assumed that O , , and Nc are xedquantities while rc(0), D0, m and n are random variables. The xed quantities O , and Nc, are assumed to have the same values as those used for the non-linear regres- sion (see Section 5.1). The random variable rc(0) is assumed to have a log-normal distribution with a mean of 180 MPa and a standard deviation of 5.4 MPa. The ran- dom variable D0 at cycle Ninspj is assumed to have a truncated normal distribution in the interval (0, 1) with mean equal to Dinspj and standard deviation equal to 0.1. This distribution of D0 is consistent with the one used to generate the statistics of m and n (see Section 5.1). The random variables m and n are assumed to have a joint lognormal distribution with the statistics given in the Section 5.1. Starting from the recording of the third inspection, the probability of macrocrack initiation calculated for different cycles is given in Table 3.It is seen from Table 3 that the probabilistic fatigue damage analysis proce- dure updates the probability of macrocrack initiation with successive inspections. The cumulative probability distribution for macrocrack initiation with inspections is shown in Figure 2.The numbers (1,., 6) in the gure indicate the cycle numbers at which inspection is recorded. Observe that immediately following an inspection, the probability of mac- rocrack initiation drops to zero. This is due to the fact that it is implicitly assumed in the probabilistic procedure that a macrocrack if present, will be denitely detected by the inspection procedure.Table 3. Calculation of Pma.CyclesPmaNs3rd Insp4th Insp5th Insp6th Insp (Ninsp = 26880)(Ninsp = 30800)(Ninsp = 33040)(Ninsp = 34000) 30,0000.093040.000000.000000.0000031,0000.155480.029220.000000.0000032,0000.227020.210270.000000.0000033,0000.304000.391660.000000.0000034,0000.381800.543300.629070.0000035,0000.458450.661480.818840.9634340,0000.743680.930520.991620.99989651243Pma - 000.511.522.533.54N - x 104Figure 2. Cumulative probability distribution for macrocrack initiation.Note that for the fatigue problem described, the rst macrocrack is observed at approximately 34,160 cycles (see Ogi et al., 2001). As seen from Table 3 and Figure 2, the formation of the macrocrack is predicted quite well.6. SummaryA methodology to predict macrocrack initiation which has the following features has been presented: use of acoustic non-linearity to
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
|
2:不支持迅雷下载,请使用浏览器下载
3:不支持QQ浏览器下载,请用其他浏览器
4:下载后的文档和图纸-无水印
5:文档经过压缩,下载后原文更清晰
|
 川公网安备: 51019002004831号
川公网安备: 51019002004831号